Профилирование высокоэффективных кулачков газораспределения двигаетелей внутреннего сгорания

Профилирование кулачков механизма газораспределения (далее – МГР) является ответственной, сложной и трудоемкой задачей. Ее решение обусловлено многочисленными, часто противоречивыми требованиями. Важнейшим из них является максимизация время-сечения клапана, так как от этого показателя, характеризующего эффективность кулачка, в значительной степени зависит качество процессов газообмена. При этом также необходимо обеспечить выполнение ряда ограничений на кинематические, динамические, прочностные, гидро-

динамические и технологические характеристики, определяющие надежность сопряжения кулачок-толкатель и МГР в целом. Последнее обусловлено тем, что МГР, наряду с кривошипно-шатунным механизмом [7], является одним из наиболее уязвимых в ДВС: на его долю приходится до 50 % от всех отказов двигателя.

Используемые обычно при разработке профиля методы имеют в этом отношении ограниченные возможности. Дальнейшее повышение эффективности кулачков достигается на основе применения численного метода профи- лирования [4–6; 10]. Рассмотрим полученные при этом результаты для случаев наличия верхнего выстоя толкателя, ограничения радиуса кривизны профиля, контактного напряжения в сопряжении кулачок-толкатель и коэффициента запаса усилия клапанных пружин.

Известно, что наличие верхнего выстоя толкателя способствует росту площади под кривой перемещения толкателя и, следовательно, время-сечения клапана. Однако, как правило, для таких кулачков характерна разрывная кривая ускорения толкателя, что ограничивает возможность их применения при увеличении частоты вращения распределительного вала в связи с ухудшением динамики клапанного привода. С целью устранения этого недостатка предложен безударный кулачок с верхним вы-стоем [3], обеспечивающий неразрывность закона изменения аналога ускорения толкателя s " (ф) по углу поворота. Однако при этом на стыке участков движения и верхнего выстоя имеется разрыв третьей производной от перемещения толкателя по углу поворота кулачка, что повышает динамические нагрузки в приводе. Это также относится к кулачкам [1; 2], у которых участок положительного ускорения образован тремя прямолинейными отрезками.

Кроме того, закон движения толкателя для указанных кулачков [1–3] на стороне подъема или опускания состоит из нескольких макроучастков и описывается заранее заданными аналитическими зависимостями (синусоидами, косинусоидами, параболами, прямолинейными участками). Так, участок положительных значений ускорения толкателя кулачка [3] описывается, как и у известного кулачка Курца, полуволной синусоиды и поэтому имеет жестко заданную форму. Это в ряде случаев ограничивает возможности совершенствования газообмена, так как, например, увеличение время-сечения клапана при неизменных фазах газораспределения или сужение фаз при неизменном время-сече-нии может привести к значительному росту максимального значения ускорения и повышенным динамическим нагрузкам [10].

Использование численного метода профилирования позволяет на протяжении всего профиля кулачка, включая сбег и верхний выстой, обеспечить непрерывность как ускорения толкателя, так и третьей производной s ′′′ от его перемещения по углу поворота кулачка (а при необходимости и производных более высокого порядка). В начале положительной ветви кривой ускорения толкателя задаются граничные условия (подъем, скорость и ускорение, а также высшие производные от перемещения толкателя по углу поворота кулачка), позволяющие сопрягать рабочий участок со сбегом. Для сопряжения участков подъема и опускания толкателя на вершине кулачка также обеспечивается выполнение требуемых граничных условий. В частном случае, принимая в качестве граничного условия на вершине кулачка s " = 5 ^m = 0 и учитывая в процессе пошагового синтеза профиля задаваемые ограничения на вторую, третью и четвертую производные, получаем закон движения толкателя, изображенный на рис. 1 сплошной линией. При этом плавность изменения ускорения, влияющая на динамические качества привода, и форма кривой ускорения на различных участках профиля легко варьируются из-

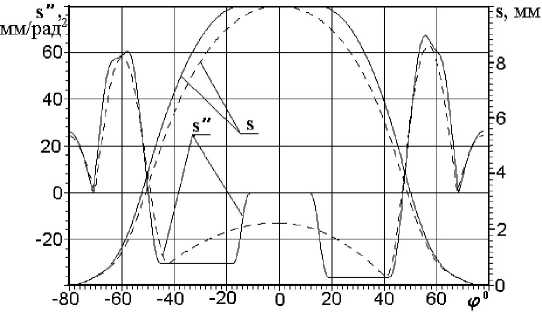
Рис. 1. Аналог ускорения s " ( ф ) и перемещение s( ф ) толкателя по углу ф поворота кулачка, спрофилированного численным методом (сплошная линия), и кулачка Курца (штриховая линия)

менением упомянутых ограничений (предельных значений) высших производных.

Численное представление закона движения толкателя позволяет отказаться от заранее принятых схем аналитического описания профиля, а способ его пошагового формирования с максимизацией в каждой точке модулей положительного или отрицательного ускорения обеспечивает предельную эффективность кулачка. При этом в процессе профилирования учитываются многочисленные ограничения на характеристики профиля, определяющие работоспособность, надежность и динамические качества привода. Например, известно, что при наличии вогнутого участка профиля его минимальный по модулю радиус кривизны не должен быть меньше радиуса поверхности толкателя (или рычага), сопряженной с кулачком. Кроме того, радиус кривизны вогнутого участка профиля кулачка не может быть меньше по модулю радиуса шлифовального круга станка, используемого для обработки распределительного вала. В связи с этим существуют способы (в ряде случаев приближенные) выбора параметров привода клапана [9], обеспечивающие выпуклость профиля кулачка. Однако для традиционных методов профилирования кулачка задаваемое ограничение на радиус кривизны профиля является активным только в отдельных точках. В то же время при использовании численного метода профилирования кривая ускорения толкателя не описывается какой-либо аналитической зависимостью, а формируется численно под влиянием тех или иных требований, что повышает эффективность кулачка, так как принятые ограничения могут быть активными на участках профиля значительной протяженности.

На рис. 1 наряду с характеристиками кулачка, спрофилированного численным методом (сплошная линия), изображены характеристики выпускного кулачка двигателя 8ЧВН15/16, спрофилированного методом Курца (штриховая линия). В обоих случаях минимальный по модулю радиус кривизны ρ вогнутого участка (на положительной ветви ускорения толкателя) равен –300 мм. Но для кулачка Курца это значение имеет место только в двух точках: на стороне подъема при ϕ = – 61° и на стороне опускания при ϕ = 59°, в то время как для кулачка, спрофилированного численным методом,

ρ = – 300 мм на протяжении двух участков: на стороне подъема при -64° <  ф <  -58° и на стороне опускания при 56° <  ф <  61°. Увеличение за счет этого общего уровня положительного ускорения толкателя и соответствующее перераспределение отрицательного ускорения с учетом верхнего выстоя толкателя способствовали росту более чем на 11 % площади под кривой перемещения толкателя (и, соответственно, время-сечения клапана) для кулачка, спрофилированного численным методом, по сравнению с кулачком Курца. При этом в обоих случаях минимальное допускаемое значение аналога отрицательного ускорения толкателя составило –30,7 мм/рад² на стороне подъема и –36,5 мм/рад² на стороне опускания толкателя.

Значение радиуса кривизны ρ при формировании профиля кулачка определяется по известным формулам в зависимости от типа и размеров элементов клапанного привода [8]. Для данного случая, при использовании рычажного толкателя двигателя 8ЧВН15/16 с цилиндрической поверхностью контакта (см. рис. 2)

р = [ R ² + ( dR / d в )²]^3,2/[ R ² + 2( dR / d в )² = - R ( d ² R / d в ²)] - R T 0

R = R 0 + R T 0 + s               (2)

где R – текущий радиус-вектор; b – угол между связанным с кулачком фиксированным радиусом-вектором (в данном случае соединяющим центр начальной окружности кулачка с его вершиной) и линией, соединяющей точки О и О ₁, через которые проходят соответственно оси вращения кулачка и цилиндрическо-й контактной поверхности рычажного толкателя; R_{T 0} – радиус контактной поверхности толкателя; R ₀ – радиус начальной окружности (затылочной части) кулачка; s – перемещение толкателя.

При этом угол b связан с углом ϕ поворота кулачка следующим соотношением:

ф = в + arccos

A ² - R T + ( R о + R_T o)^{2 2} A ^{( R} 0 ⁺ R T 0 )

- arccos

A ² - R T + R²

2 AR

где A – расстояние между осями вращения кулачка и качания толкателя; R_T – радиус качания толкателя.

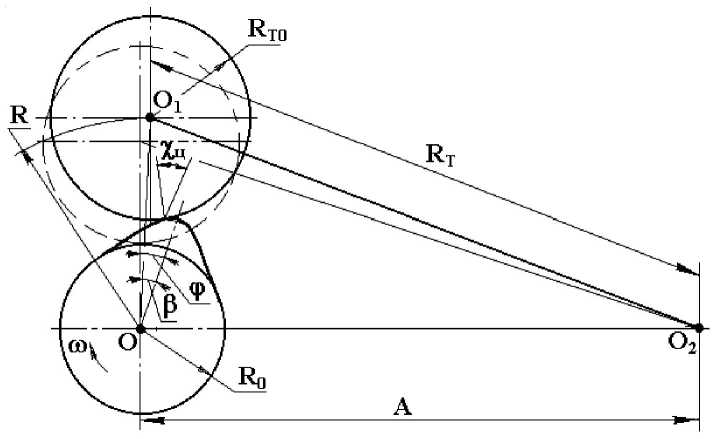
Рис. 2. Схема кулачкового механизма с рычагом, имеющим цилиндрическую поверхность контакта

Следует отметить, что авторами [1; 2] предлагалось также составлять участок положительного ускорения из двух наклонных прямолинейных отрезков, сопряженных параболой в области максимальных ускорений, с целью увеличения площади под кривой перемещения толкателя при ограничении радиуса кривизны вогнутого участка профиля. Это может приблизить получаемый при этом профиль кулачка к предельно эффективному, но не позволяет его достигнуть. К тому же весьма сложно подобрать параметры такого участка положительного ускорения толкателя, в наибольшей степени приближающие этот профиль к оптимальному, получаемому численным методом. Эта задача усложняется также и потому что характер изменения ускорения в области максимальных значений при ρ = – 300 мм неодинаков для участков подъема ( - 4° <  Ф < - 58°) и опускания (56° <  ф <  61°) толкателя (см. рис. 1, сплошная линия). Последнее обстоятельство связано с тем, что на характер изменения ускорения при активном ограничении на радиус кривизны профиля существенно влияют размеры и особенности конструкции клапанного привода. Так, рассматриваемый тип толкателя характеризуется асимметрией закона качания рычага на сторонах подъема и опускания при использовании симметричного кулачка.

Сказанное относится и к результатам профилирования кулачка, полученным при ограничении контактного напряжения σ в сопря- жении кулачок-толкатель. Величина σ также может быть вычислена в любой точке профиля по известным формулам. Например, для рычажного толкателя с цилиндрической поверхностью контакта о = 0,59

I Q (1/ Р + 1/ R t о ) b (1/ E K + 1/ E T )

Q = ( P₀ i + csi ² + Ms" to ²i²)/cos x ц (5)

где Q – сила в контакте кулачок-толкатель, направленная по нормали к профилю; b – длина линии контакта; E_K и E_T – модули упругости материалов кулачка и толкателя; P ₀ – начальное усилие клапанных пружин (при s = 0); i – передаточное число коромысла; с – жесткость клапанных пружин; M – масса движущихся частей механизма, приведенная к клапану; ω – угловая скорость вращения распределительного вала; χ _ц – угол давления для центрового профиля кулачка.

На рис. 3 сплошной линией приведены характеристики профиля кулачка, спрофилированного численным методом при ограничении σ £ 340 МПа для схемы и размеров клапанного механизма двигателя 8ЧВН15/16. При этом на участке значительной протяженности –39° £ ϕ £ 43° указанное ограничение σ является активным, и величина контактного напряжения равна предельно допускаемому значению 340 МПа. Штриховой линией приведены характеристики профиля кулачка той же угловой протяженности, у которой участок отрицательного ускорения толкателя сформирован при ограничении аналога минимального ускорения s" > -14,2 мм/рад2 таким образом, что величина контактного напряжения также не превышает 340 МПа. Однако при такой форме отрицательной ветви кривой ускорения толкателя предельно допускаемое значение σ достигается только в одной точке - на вершине кулачка при ф = 0°, а на участках значительной протяженности -49° < ф < -19° и 16° < ф < 49° уменьшен модуль отрицательного ускорения, что привело к уменьшению наибольшего подъема толкателя на вершине кулачка до 9,52 мм и снижению более чем на 5 % общей площади под кривой перемещения толкателя и время-сечения клапана.

Характер изменения ускорения толкателя по углу поворота кулачка при активном ограничении на контактное напряжение зависит от радиуса кривизны профиля, усилия клапанных пружин, конкретных размеров и конструктивных особенностей клапанного привода. Поэтому существующие традиционные методы профилирования, основанные на заранее заданных способах аналитического описания закона движения толкателя, позволяют профилировать кулачки, лишь в той или иной степени приближающиеся по эффективности к предельным кулачкам, получаемым численным методом. Следует также отметить, что выравнивание значений контактного напряжения в сопряжении кулачок-толкатель по углу поворота кулачка при использовании числен- ного метода профилирования позволяет получить равнопрочный профиль в области наибольших значений σ .

Важным условием, которое необходимо учитывать при профилировании кулачков МГР, является обеспечение неразрывности звеньев клапанного механизма в процессе его работы. При недостаточной величине коэффициента запаса усилия клапанных пружин к, равного отношению действующей силы пружин к силе инерции движущихся частей механизма, приведенной к клапану, возможен разрыв кинематической цепи и неуправляемое движение клапана, в особенности при наличии интенсивных колебательных процессов в механизме. В связи с этим в ряде известных методов профилирования кулачков [1–3] предлагается такое аналитическое описание кривой ускорения толкателя по углу поворота кулачка в наиболее опасной зоне отрицательных значений ускорения, при котором модуль последнего плавно увеличивается по мере роста силы пружин в процессе ее деформации. Однако наиболее просто и точно эта задача может быть решена при использовании рассматриваемого численного метода профилирования кулачка. В процессе формирования участка отрицательного ускорения, где разрыв кинематической цепи наиболее вероятен, значение коэффициента к вычисляется по формуле к = -(P0+ csi)/(Ms" го2 i). (6)

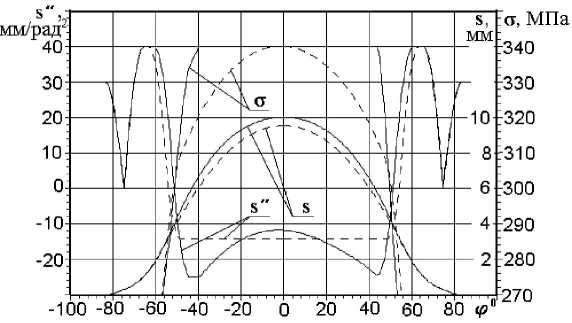
Рис. 3. Характеристики профиля кулачка по углу ф его поворота: аналог ускорения s " ( ф ), перемещение s ( ϕ ) и контактное напряжение σ ( ϕ )

На рис. 4 сплошной линией приведены характеристики профиля кулачка, спрофилированного численным методом при ограничении к >  3 для схемы и размеров клапанного механизма двигателя 8ЧВН15/16. При этом на участке значительной протяженности -24° <  ф <  24° указанное ограничение к является активным, и величина коэффициента запаса усилия клапанных пружин равна минимальному допускаемому значению. Штриховой линией приведены характеристики профиля кулачка той же угловой протяженности, у которого участок отрицательного ускорения толкателя сформирован при ограничении аналога минимального ускорения s " > -30,5 мм/рад² таким образом, что величина коэффициента запаса усилия клапанных пружин также не меньше трех. Однако при такой форме отрицательной ветви кривой ускорения толкателя предельно допускаемое значение к достигается только в двух точках: на стороне подъема при ф = -25° и на стороне опускания при ' ф = 25°, а на участке значительной протяженности -25° <  ф <  25° уменьшен модуль отрицательного ускорения, что привело к уменьшению наибольшего подъема толкателя на вершине кулачка до 8,8 мм, и снижению более чем на 8 % общей площади под кривой перемещения толкателя и время-сечения клапана.

Выполненные исследования показали преимущества численного метода профилирования по сравнению с традиционными при наличии и других требований (по гидродинамическим условиям смазки сопряжения кулачок-толкатель, углу давления), а также в случае использования разрывной кривой ускорения. Этот метод был использован при разработке кулачков для ряда автомобильных и тракторных двигателей. Полученные результаты свидетельствуют о том, что он позволяет на основе единого подхода проектировать предельные по эффективности кулачки с учетом различных ограничений на их характеристики.