Профильная проходимость легких колесных вездеходов под пологом леса

В общем случае под проходимостью понимают эксплуатационное свойство машины, определяющее возможность ее перемещения в конкретных условиях, в том числе при преодолении различных препятствий. Поскольку эксплуатационные условия для машин совершенно неодинаковы, то до сих пор нет единого определения проходимости для различных машин, очевидно, его и не может быть. Также отличаются показатели, по которым производится оценка проходимости различных машин. Применительно к автомобилям, например, профильную проходимость в соответствии с ГОСТ 22653-77 оценивают по следующим единичным показателям: дорожному просвету, переднему (заднему) свесу, углу переднего (заднего) свеса, продольному радиусу проходимости, наибольшему углу преодолеваемого подъема, наибольшему углу преодолеваемого косогора. Для полноприводных автомобилей в соответствии с РТМ 37.001. 039-77 основными измерителями профильной проходимости является ширина преодолеваемого в поперечном направлении рва и высота преодолеваемой вертикальной стенки [1].

Исследование профильной проходимости вездехода при его движении под пологом леса, разработка новых более совершенных методик ее анализа является весьма актуальной проблемой для практики, потому что ее решение неразрывно связано с возможностью выполнения машиной ее технологических задач в условиях производства.

Проблема изучения процесса передвижения машины под пологом леса появилась со времени внедрения транспортных машин в технологический процесс лесозаготовок, то есть с середины прошлого века. Ее решению посвящены работы таких ученых, как И.М. Бартенев [2], М.Г. Бергер [3], В.И. Прядкин [4], С.Г. Жендаев [5] и др. Однако ряд вопросов по анализу проходимости машин под пологом леса, о влиянии на проходимость конструктивных параметров лесных машин и условий эксплуатации являются до сих пор неизученными.

Недостаточная изученность вопроса о передвижении транспортно-технологических машин под пологом леса объясняется в немалой степени отсутствием методик оценки вероятности преодоления участка леса, адекватно отражающих движение вездехода. В данном случае особое значение приобретает вопрос выбора критерия оценки проходимости.

При движении машины под пологом леса физический смысл понятия “профильная проходимость” заключается в нарушении возможности перемещения вездехода в выбранном направлении в результате его взаимодействия с непреодолимым препятствием – деревом. В итоге при низкой профильной проходимости вездеход в условиях лесопродукционного производства не может выполнять технологические функции вообще. При этом возможность перемещения вездехода без встречи с деревом количественно можно оценить через вероятность преодоления участка местности, покрытого деревьями. Исходя из вышеизложенного, профильную проходимость, выраженную через вероятность преодоления участка лесистой местности, можно выделить как наиболее важное эксплуатационное качество машины и принять его в качестве критерия при обосновании параметров легких вездеходов при их использовании в условиях лесопродукционного производства.

Нами рассматриваются математические модели для оценки проходимости легкого вездехода по участку местности под пологом леса с учетом его размеров, его формы в плане способа управления, маневренности и плотности расположения деревьев.

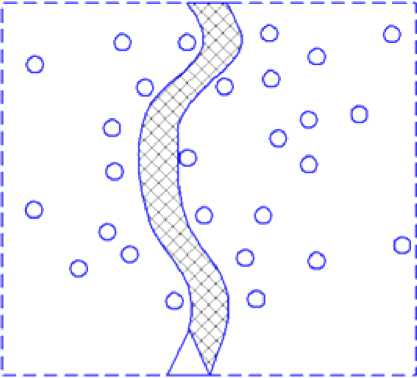
△ - вездеход шириной b

О - деревья в ко личестве .\'_шт радиусом R^

U - пробная п лощадь, S_o

□ - площадь, покрываемая вездеходом при движении, S

Рис. 1. Схема движения вездеходапод пологом леса

В качестве инструмента исследований предложен метод анализа, который основан на изучении взаимодействия горизонтальной проекции вездехода на плоскости при его перемещении под пологом леса с нанесенными на ней препятствиями – деревьями (рис.1), то есть на взаимодействии плоских фигур на плоскости.

В общем виде задачу можно сформулировать следующим образом: определить вероятность продвижения вездехода на расстояние L , если известно количество деревьев N на пробной площади 5 0 , средний радиус дерева R 0 и ширина вездехода Ь .

В данном случае движение вездехода можно представить в виде цепочки последовательно выполняемых перемещений с определенным шагом.

Причем при совершении очередного шага возможно движение как прямо, так и с поворотом налево или направо.

При этом движение возможно лишь в том случае, если на пути вездехода не будет деревьев.

Также вездеход может быть ограничен в совершении маневров, когда он останавливается при встрече с первым же деревом, а может обладать повышенной маневренностью, когда при

встрече с деревом он может сделать один шаг назад, выбрать новый путь и продолжить движение.

Решение задачи основано на том, что вероятность отсутствия точечных препятствий Р(0) или деревьев при R 0 = 0 на площади 5 , которую покрывает вездеход при движении, составляет e ^-s'^p или

es'P ’ где р =--плотность деревьев на участке. Если же R0 > 0, но R0 << Ь, что больше соответствует реальности, задачу можно свести к случаю, когда R0 = 0, считая ширину вездехода, равной Ь0 = Ь + 2Ro.

Как отмечено выше, перемещения вездехода на расстояние, равное AL , можно достичь тремя способами: движением вперед на AL ; поворотом влево относительно заднего левого колеса; поворотом вправо относительно заднего правого колеса. При этом в соответствии с теорией вероятностей для вычисления вероятности сдвига на один шаг хотя бы в одном из направлений необходимо знать вероятности сдвига вперед, налево и направо, а также вероятности сдвига в двух и всех трех направлениях (рис. 2, вариант трехколесного вездехода).

Расчет вероятности перемещения на один шаг P(ДL) ведется по формуле вероятности суммы совместных событий:

P( △ L) = Р прав

+ ^Р лев + ^Р пр

[ ^Р лев , пр ^{+ Р} прав , пр ^{+ Р} прав , лев ] ^{+ Р} общ ,

где Р прав , Р лев , Р пр , Р лев , пр , Р прав , пр , Р прав , лев , Р общ - соответственно вероятность перемещения вездехода на один шаг направо, налево, прямо, сочетание движений налево и прямо, направо и прямо, направо и налево, сочетание движений влево, направо и вперед.

Для определения вероятности перемещения на один шаг необходимо рассчитать площадь, покрываемую вездеходом при перемещении в каждом направлении, подставить полученные значения площадей в формулу (1) и произвести необходимые вычисления с учетом плотности расположения деревьев на участке. Затем полученные вероятности требуется подставить в формулу (2) для определения вероятности суммы совместных событий и рассчитать вероятность совершения одного шага.

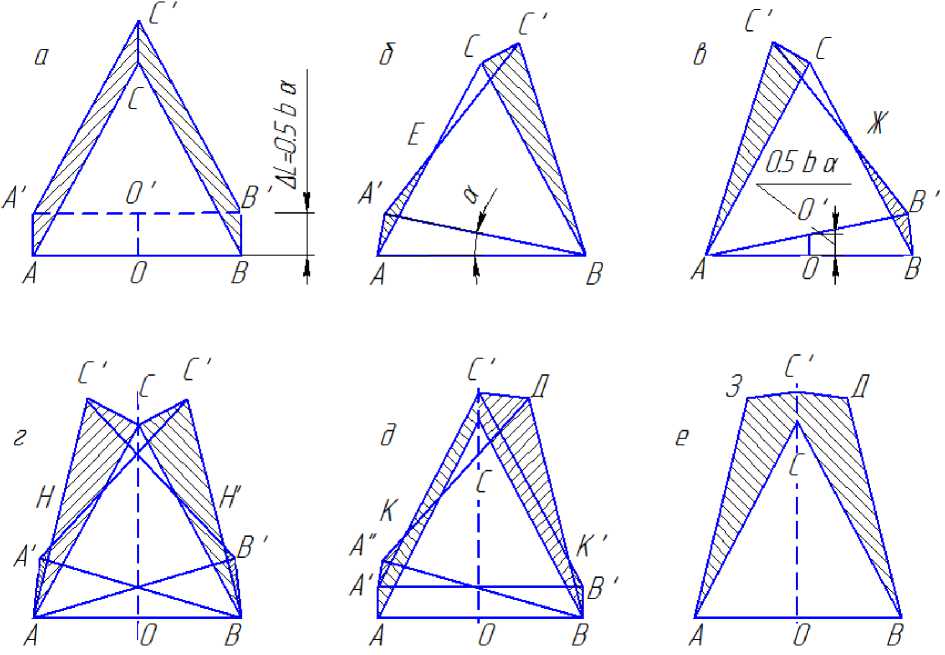
Рис. 2. Схемы возможных перемещений трехколесного вездехода при расчете вероятности сдвига на один шаг: а – движение прямо; б – движение направо; в – движение налево; при сочетании движений: г – налево и направо; д – направо и вперед (или налево и вперед); е – направо, налево и вперед (заштрихованы зоны, свободные от деревьев для осуществления перемещения вездехода)

В итоге получена зависимость для расчета вероятности перемещения трехколесного вездехода на один шаг:

P(M} = 2е

-О,5Ь 0 ^а

(1+зТз-аЛ UvWp

+ _e—O,5b-b_o-_a-p + _e ^-2b^^a(l+ 2 ⁺v^}p - _-2e -b-iw(x25

^-b²a {l^} Р е^                                    .

+^}

2   8

-

Как видим, параметрами, определяющими свободное движение вездехода при перемещении на один шаг, являются ширина вездехода Ь , плотность расположения деревьев р и их диаметр.

Как показывает анализ, для реальных значений входящих в формулу (3) параметров, эта вероятность составляет более 90 %.

Для продвижения же на расстояние L необходимо последовательно сделать п = ^- таких шагов. Вероятность того, что ни на одном шаге движение не будет остановлено P( L), определяется по формуле:

Р(L)=[P(∆L)]L/∆L.

Как показывают расчеты, вероятность преодоления участка леса при ограничении маневренности вездехода, что предопределяется отсутствием передачи заднего хода в его трансмиссии, составляет ничтожную величину в связи с возведением в высокую степень числа, меньшего единицы.

Действительному движению больше соответствует задача о выборе пути заранее в пределах обзора местности водителем или, когда при возникновении на пути непреодолимых препятствий в виде деревьев вездеход может сделать один шаг назад с целью найти другой путь.

Возможность такого маневра обеспечивает наличие в силовой передаче вездехода заднего хода.

При высокой маневренности вездехода и, если Р лев , Р пр >  0,33 , где Р _лев = e~^{sлев Р} , Р пр = e~^s прям ^Р - вероятности перемещения на один шаг налево и прямо, то вероятность Р проезда машины на любое расстояние не зависит от этого расстояния и является решением уравнения:

1 -p = (1 -РлевР)(1 — Рпр p).

В этом случае решение задается формулой:

Р =   + ^(1 "J1+ 4  (1 -Рлев)),

Рлев    2* пр \      \       *пев/ где движение вездехода при этом теоретически достоверно.

Структурно легкий вездеход может быть выполнен трехколесным, представляющим в плане треугольник, а также четырех- или шестиколесным, представляющим в плане прямоугольник. Вездеход, имеющий в плане прямоугольник, может быть выполнен как с жесткой рамой, так и с шарнирно-сочлененной (ШСР). Поворот вездехода с жесткой прямоугольной рамой осуществляется за счет поворота его передних управляемых колес, поворот вездехода с ломающейся рамой осуществляется за счет складывания полурам.

Поскольку при расчете вероятности преодоления участка местности под пологом леса фигурирует площадь, покрываемая вездеходом при движении, то была выдвинута гипотеза о влиянии формы вездехода в плане и способа его поворота на профильную проходимость.

В результате выполненного анализа получены математические модели (табл.) для оценки проходимости для различных условий движения и различных конструкций вездехода. В этом случае решение независимо от формы вездехода задается формулой (6), но составляющие этой формулы для разных вездеходов в плане будут различны, что предопределяет в итоге разные результаты для различных вариантов исполнения вездехода.

Математические модели для сравнительной оценки профильной проходимости под пологом леса

Вариант исполнения вездехода	Математическая модель
Четырех-или шести-	где		Р^ = ^ + f(1 - J1+ ^ (1 - Р лев )) • Р лев 2tn p \     \       Р лев              / Р пр = e~s1P; $ 1 = (b + d)l; Р лев = e~s2P;
колесный с жесткой рамой		$ 2	1Г , / .    . ^ \             а2sin(a + Ю] . „ „ = 2 |а 2 (ctga + - 2 ) + b 2 tga --—--------1 + dl - $0; l
			$0 = ba; р
				bctga - 0,5a
Четырех-			Р(^ = — + —(1 Р пев     2Р пр\	- /1+ ^ (1 -Р лев )) . \      rлев              /
или шестиколесный	где	Р пр = e	-^ •Р ; $ 1 = (b + d)l ; Р лев = e~S^P ; $ 2 = $ пов + $ сегм ab + 0,5а (b - 0,5bctg ^ + Л + 0,5d) - (0,5b - Atg ^) ctg ^
с шарнирно-		$ пов =
сочленен-		, . а
ной рамой	$ сегм	/^ 2h	а 2bh ctg — + (h- A) 2 + d 2	|(h ctga + b ) + (h-A) + h ctg^ + b
Трехколесный	где	$ 2 =	Р(^) = ^ + f(1 - J1 + ^ (1 - Р лев )) , Р лев 2Г пр \     \       Р лев              / Р пр = e~s1P ; $ 1 = (b + d)l ; Р лев = e~s^P 0,5 a \(l seca + a ctga)coseca + b (-^ -5 — 1)1 + dl 1 v                                        \sin a     /1

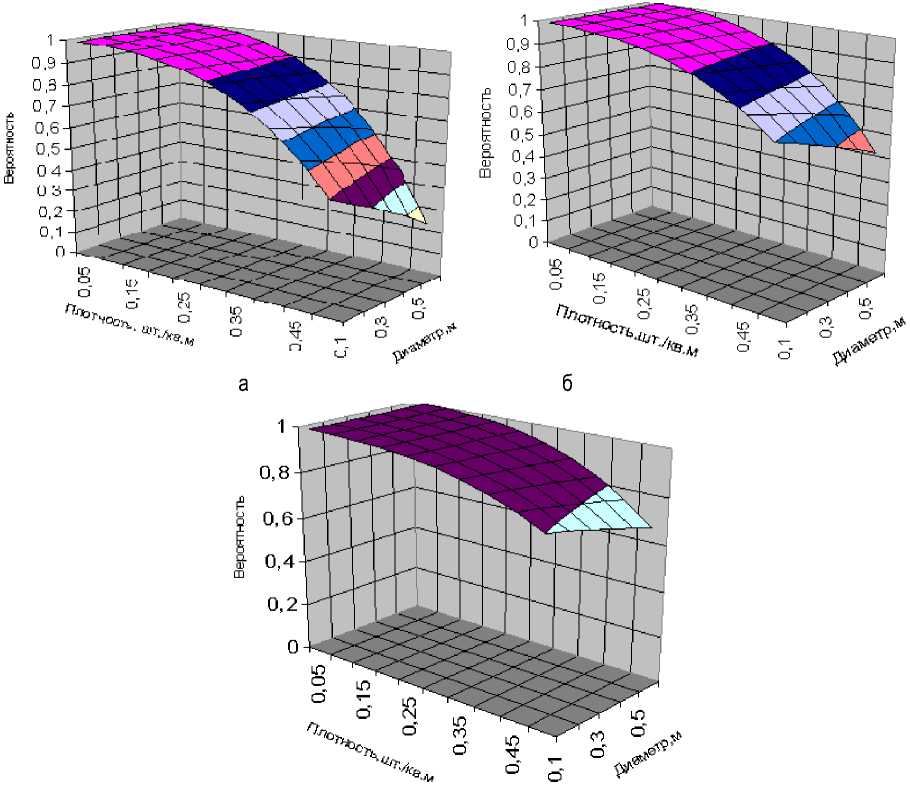
По представленным моделям для трех анализируемых вариантов исполнения вездехода были рассчитаны вероятности перемещения на 50 м вездехода шириной b = 2,3 м , длиной а = 3,5 м и построены графики (рис. 3).

Данные, представленные на рис. 3, свидетельствуют о том, что при высокой маневренности вездехо- ды имеют вероятность преодоления участка лесистой местности более 0,9 при плотности расположения деревьев не более 0,23-0,27 шт/м2, что говорит о том, что движение вездехода теоретически достоверно. Причем более высокую проходимость имеют вездеходы с треугольной рамой, т.е. трехколесные, далее идут четырёх- или шестиколёсные с жёсткой прямоугольной рамой и немного уступают им четырёх- или шестиколёсные вездеходы с шарнирно-сочлененной рамой. Разница в проходимости нивелируется при снижении плотности расположения деревьев.

в

Рис. 3. Вероятность преодоления участка лесистой местности: а – четырёх- или шестиколёсным вездеходом с ШСР; б – четырёх- или шестиколёсным вездеходом с жёсткой прямоугольной рамой; в – трёхколёсным вездеходом

Для практических целей большую значимость представляет задача по определению ширины вездехода для заданной плотности расположения деревьев и вероятности преодоления участка местности под пологом леса.

Условие задачи можно интерпретировать следующим образом: известна плотность расположения деревьев р на участке лесистой местности, необходимо подобрать максимально возможную ширину вездехода b для заданной вероятности преодоления этого участка Р , чтобы выполнялось условие:

Р = 1 - (1 - Р лев Р)(1 - Р пр Р)(1 - Р прав Р)

Решая это уравнение и подставляя вместо радиуса дерева R₀ его диаметр d , получаем выражение для определения ширины вездехода:

b = 12йуы+¹⁶²⁸^ы^^ - 1,705d .               (8)

p      1-3/1—p

Выводы

• 1.    При анализе профильной проходимости вездехода под пологом леса в качестве критерия целесообразно использовать такой показатель как вероятность перемещения вездехода на определенное расстояние.

• 2.    В статье предложен метод анализа профильной проходимости, основанный на изучении положения плоских фигур на плоскости.

• 3.    Параметрами, определяющими свободное движение вездехода при перемещении на один шаг, являются ширина вездехода, плотность расположения деревьев и их диаметр.

• 4.    Для повышения профильной проходимости при движении вездехода под пологом леса целесообразно его трансмиссию оборудовать передачей заднего хода.

• 5.    Трехколесный вездеход имеет определенные преимущества по профильной проходимости по сравнению с четырех- или шестиколесным вездеходом.