Прогибы стальной балки, предварительно напряженной изгибом тавра

Предварительно напряженная стальная двутавровая балка изготавливается путем присоединения к изгибаемому тавру, сваренному из стенки и пояса, второго поясного листа. На начальной стадии тавр изгибается двумя сосредоточенными силами Р , так что по сечению элемента возникает зона чистого сдвига и чистого изгиба. При этом балка получает выгиб f 0t (рис. 1а).

Для решения задачи по нахождению величины прогиба балки на стадии изготовления воспользуемся дифференциальным уравнением изогнутой оси балки: d2y = - Mx . dx2    EIxt

Значения изгибающего момента балки будут равны:

при x < a; M_x = Px.

— =---— [ Mxdx =---— [ Pxdx dx EIxt x EIxt

Г 7

1 Px 2 —

EIxt 2

xt ^

⁺ C 1

J

У =

EIxt

J

Px ²

— +

^

C 1 dx =

J

EIxt

-x - + C x + D

J

При x > a ; M x =Px - P(x - a)

dy dx

—

-^-J^{[ P}x ^{— P} ( ^{x —} a ^{)] dx} =

EIxt

—

Px ²

EIxt I

P ( x — a )²

)

+ ^C 2 J

У =

1 r( Px ² P ( x — a )²

Er; ^Jl -^—

+ C 2 dx = J

jL ( Px;

EIx, I 2

P ( x — a )²

)

+ C 2 x + D 2 J

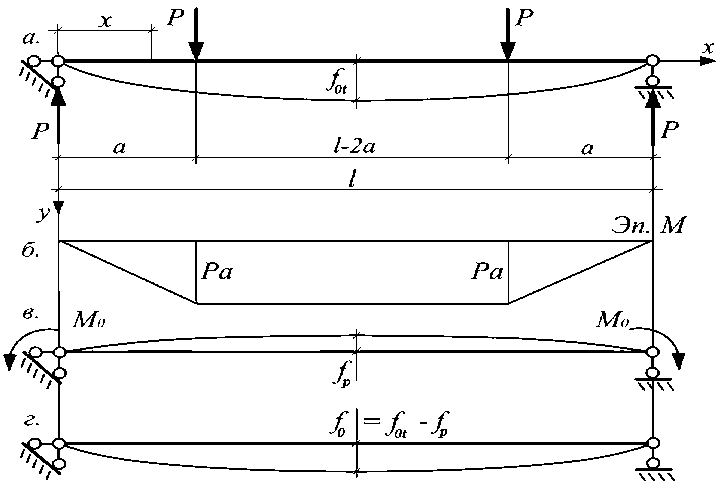
Рис. 1. Прогиб балки на стадии предварительного напряжения:

а - схема загружения и начальный выгиб исходного тавра на стадии изготовления балки; б - эпюра изгибающих моментов на стадии изготовления балки; в - изгибающий момент и прогиб двутавра после снятия усилия предварительного напряжения;

г - результирующий выгиб двутавра на стадии предварительного напряжения

Принимаем граничные условия x = 0 ; y = 0 . При условии x < a , D 1 = 0 .

Постоянная интегрирования D1 характеризует прогиб оси стержня. Поскольку прогиб будет один и тот же при условии x < a; Mx = Px и x > a; Mx=Px-P(x- a), то можно записать, что D1 = D2.

При условии x > а прогиб оси y будет максимальным при x = L, поворот сечения можно записать как 01 = dy = о.

dx

Это условие будет иметь вид:

dy 1

—

dx    EIxt

' p¹!

2 4 V

—

P I -

2 V 2

—

А² _ ¹ a I + С 2 = 0 ,

7 J

откуда

_ _ P ( l — 2 a )² Pl^г Сз = .

22      4       8

Подставив полученное значение С 2 в выражения (1) — (4), получим:

dy =__ L ( Px ² ₊ P ( - — 2 a )2 _— PL 2

dx EIxt V 2        8        8

y =

EIxt

Px ³

( Px ²

+ x I--+

I 2

P ( l — 2 a )²

Pl ² 1

dy _    1 ( Px ² P ( x — a )² P ( l — 2 a )²    Pl ² 1

= 1 1

dx    EIxt V 2        2           8        8 J y =

EIxt

Px³ P ( x — a )³     | P ( l — 2 a )² Pl²

+ x I

6        6 V 8        8

Для проверки полученных зависимостей запишем поворот сечения как

0 = dy dx

при

x=0 . Из выражения (5) значение 0 1 будет равно:

⁰ 1 = ^—

1 I P ( l — 2 a ) ²

—

EI x- V

Pl 2 8

—

Pci PPP- ( a — l ).

2 EI x-

Полученная зависимость полностью совпадает со значением поворота сечения, представленного в справочной литературе.

Величина начального выгиба fa в середине пролета балки при x -^ будет определять- ся из выражения (6) как:

f =

^{J о -}      EI x-

Pl3

—

P I - 6 1 2

—

a 1 '

+ -

l f P ( l — 2 a )

V 8

1² Pl ² — 8

,

и после некоторых преобразований получим:

f о - = Е °* ’ ^{— 4 a} ’^

где EI_x- - изгибная жесткость тавра; I_x- - момент инерции сечения исходного тавра.

Ранее в [1] было получено соотношение между моментами инерции сечений тавра I_xt и двутавра I_x как т . = Ix , откуда выражение (7) можно записать как:

x 2

f о - = fa (' l 2 — 4 a =).

12 EI x

После присоединения второго пояса к исходному тавру и снятия приложенного усилия балка пытается вернуться в первоначальное положение, при этом двутавр изгибается моментом M о = Pa. В результате происходит некоторая потеря предварительного напряжения в балке, а начальный выгиб балки уменьшается на величину f_p (рис. 1в).

Дифференциальное уравнение изогнутой оси балки можно записать как:

d ² y _ M о .

dx   Efa dy =   JM о dx = -^( M о + C);

dx EIx          EIx

У = "I" J ⁽ M о ⁺ C ) dx =

—

(    „ 2

x

Граничные условия будут равны:

-- M _o — + Cx + D I ^о

V ²           7

EI x

x = 0 ; y = 0.

x = l ; y = 0.

D = 0 .

—°— + Cl = о . Откуда

C = —

Ml

——. Тогда

0 1 = 0 2 =

x

Значение величины f _p при x = ^ будет равно:

M S- ( 2 x — l).

2 EI_x

fp  EL.

¹   M о x

—

M о xl _ M о l

—

^x v

²      Pal l-

—

8 EI_x    8 EI_x

.

Результирующий выгиб балки на стадии предварительного напряжения (рис. 1г) будет равен:

Pa ,2 _д 2x Pal Pa /,472 n 2x

f o = f o t — fn =------ (' l — 4 a )-- =------ (' l — 8 a ).

0 VO ^{- p}p 12 EIxx             8 EI_x   24 EI_x

Потери величины выгиба балки на стадии изготовления балки могут быть оценены коэффициентом у , равным:

V = A. = _a5_ (3 i 2

f 0 t 24 EIx

-

8 a ²)/ -Pa- (3 l ² -4 a ²) = 3y

12 EI_x              6 l ²

-

-

8 a ²

8 a ^{2 .}

При a = —, v = 0,345; при a = —, V = 0,455.

Под действием внешней эксплуатационной нагрузки (примем нагрузку равномерно распределенной) балка получает прогиб f q (рис. 2б), который будет равен:

_f = 5 ql ⁴ = 5 M q l ^{2 f q} = 384EI_x = 48 EI x ^,

где q – равномерно распределенная погонная нагрузка на балку; М q – момент внешней нагрузки; EI x – изгибная жесткость двутавра; I x – момент инерции сечения предварительно напряженной балки; Е – модуль упругости стали.

Значения М 0 , М q и I x получены в [2] и могут быть записаны как:

M0 = Pa = 0,1275Ry Аh; Mq = 0,4914Ry Ah; Ix = 0,1656Ah 2, где Ry – расчетное сопротивление малоуглеродистой стали С235; А – площадь поперечного сечения балки; h – высота сечения балки.

Подставив в выражение (9) значения М q и I x , получим:

0 , 4914R Ahl ²         R l ²

f_q = -        Ц = 0 , 309 y .

^q 48 0 , 1656 Ah ² E         Eh

Подставив полученное значение для М 0 в выражение (8), получим выражение:

M_n ,    ,    0,1275 RA    ,    ,        R (3 l ² - 8 a ²)

f = -M ^- (3 l ² - 8 a ²) = —----- y ----(3 l ² - 8 a ²) = 0,032   ---------

.

⁰  24 EI            0,1656 Ah ²24 E                    Eh

Суммарный максимальный прогиб f max предварительно напряженной балки от действия внешней нагрузки (рис. 2в) будет равен разности прогиба от внешней нагрузки и обратного выгиба балки.

RI ²           R_v (3 l ² - 8 a ²)

f™ = f - fo = 0,309 y--0,032--------, max q 0         Eh              Eh после преобразований величину суммарного прогиба можно записать как:

R fmax = 77 (0,21312 + 0,256a2).                                   (10)

Eh

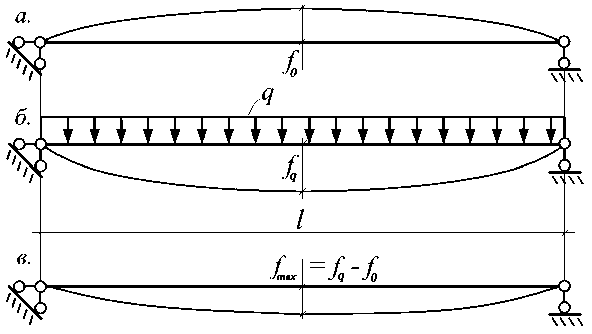
Рис. 2. Прогиб предварительно напряженной балки от действия внешней нагрузки: а - результирующий обратный выгиб балки на стадии предварительного напряжения; б - схема загружения балки и прогиб от действия внешней нагрузки;

в - суммарный максимальный прогиб предварительно напряженной балки

Подставив в полученное выражение (10) некоторые значения величины а (см. рис. 1а), получим:

при a = -, при a = -,

Rv Г      7         /2)

fm ca= 0-309 — 0-21312 + 0-256 -   = 0-241

^max Eh              9Eh

V7

f max

R 0 , 309 ^y

Eh

Г                     7 2 ^

0 - 213 1 ² + 0 - 256—

16 .

R l ²

= 0 - 229 Eh

.

Эффективность предварительного напряжения при изменении расстояния а от опоры балки до точки приложения нагрузки Р может быть оценена коэффициентом £, который определяется отношением величины прогиба от действия внешней нагрузки обычной стальной балки fq и величины прогиба предварительно напряженной балки fmax.

При

l a = 3,

^ =

при

l a = 4,

H =

f           R l ²         R l ²

= 0 - 309 ^— / 0 - 241      = 1 - 28 ;

fmax        Eh        Eh f           R l2        R l2

"' = 0 - 309 ^— / 0 - 229     = 1 - 35 .

f_max        Eh        Eh

На основании всего вышеизложенного можно сделать следующие выводы:

• 1.    Уменьшение величины начального выгиба на стадии изготовления балки вследствие некоторых потерь предварительного напряжения составляет от 34 до 45 %, в зависимости от места приложения нагрузки Р .

• 2.    Обратный выгиб балки, предварительно напряженной изгибом тавра, снижает величину прогиба от действия внешней по отношению к прогибу обычной стальной балки от 28 до 35 %.

• 3.    Полученные выражения справедливы для определения прогиба балки, предварительно напряженной изгибом тавра с шарнирным закреплением опорных узлов.