Прогноз энергопотребления в АСКУЭ ННЦ искусственной нейронной сетью

Введение. Конечной целью энергосбережения является сокращение затрат абонента на оплату энергоресурсов. У потребителей электроэнергии имеется ресурс сокращения расходов путем исключения оплаты штрафов за нарушения договорного графика потребления [1]. Поэтому потребители заинтересованы иметь в распоряжении средства мониторинга текущего потребления и прогнозирования будущего потребления.

Согласованные поставщиком и потребителем графики поставок энергоресурсов могут иметь различную протяженность во времени. Например, в периоды утреннего и вечернего максимумов энергосистем поставщики контролируют потребления на получасовых интервалах. На таких малых интервалах в качестве модели для аппроксимации графика нагрузки и его прогноза могут успешно использоваться простые (полиномиальные) разложения [2]. Для прогноза на длительных временных интервалах такие модели непригодны вследствие сложной формы графика нагрузок, содержащего к тому же стохастические компоненты. Представление таких данных в виде разложения по базису небольшой размерности оказывается невозможным. В таких случаях приемлемую точность аппроксимации и основанного на ней прогноза обеспечивают различные авторегрессионные методы [3, 4]. В последнее время разработаны эффективные процедуры, основанные на сингулярном спектральном анализе.

Перечисленные выше методы обладают существенным недостатком — их применение требует диалогового участия аналитика. Поэтому необходимо использовать более конструктивный метод, минимизирующий участие специалиста в работе процедур построения прогноза. Ниже описан пример использования с этой целью искусственной нейронной сети прямого распространения (персептрона, по Ф. Розенблату [5]).

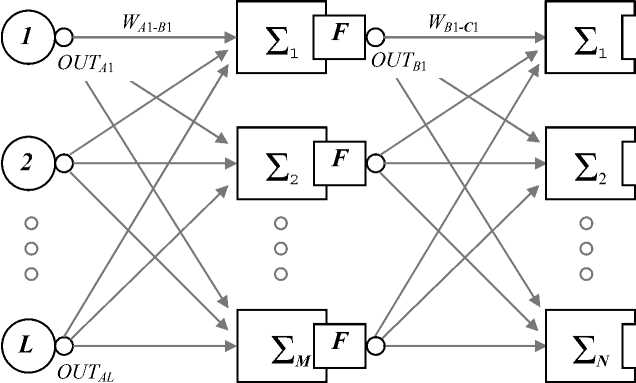
Описание модели. Многослойный персептрон представляет собой сеть, состоящую из нескольких последовательно соединенных слоев нейронов. На низшем уровне иерархии находится входной слой сенсорных элементов x 1 ,... ,x _L , задачей которого является только прием и распространение по сети входной информации. Далее имеется один или (реже) несколько

F

Функция активации

1-й слой нейронов ( В )

2-й слой нейронов ( С)

Сумматор

Сумматор

Входной слой ( А )

X 1

X 2

X L

F

F

F

Рис. 1. Структура нейронной сети

Выход

О

Выход

О

Выход

О

скрытых слоев. Каждый нейрон на скрытом слое имеет несколько входов, соединенных с выходами нейронов предыдущего слоя или непосредственно с входными сенсорами x ₁ , . . . , x _L , и один выход. Выходы нейронов последнего, выходного слоя описывают переработанный сетью результат.

Нейроны каждого слоя не связаны между собой и взаимодействуют лишь с нейронами предыдущего и последующего слоев. Каждый нейрон суммирует поступающие к нему сигналы от нейронов предыдущего уровня иерархии с весами, а затем с помощью функции активации преобразует результат суммирования.

Функция активации F ( £ ) обеспечивает нелинейность, необходимую для сходимости процесса обучения. Выходной сигнал нейрона задается выражением

OUT = F ( ( ) = 1 / (1 + exp( -( )) ,

L где ^ = У^ XkWk; Xk — входы нейрона; Wk — синаптические веса входов; L — количество k-1

входов нейрона. В качестве функции активации выбран сигмоид.

Структура используемой в настоящей работе нейронной сети представлена на рис. 1. Использованы следующие обозначения:

• —    каждому слою нейронной сети соответствует своя буква (например, входному слою соответствует буква A , выходному — C ;

• —    нейроны каждого слоя пронумерованы арабскими цифрами;

• —    Wa 1 - в 1 — синаптический вес между нейронами A 1 и B 1;

• —    OU T _{A 1} — выход нейрона A 1.

Прежде чем использовать нейронную сеть для получения прогноза, ее необходимо обучить, т. е. определить синаптические веса. Для обучения персептронов часто используется детерминистический метод обратного распространения ошибки [6]. Этот метод предполагает априорное знание множества требуемых значений выходов нейронов последнего слоя сети, называемых целевыми, при заданном множестве входов начального (нулевого) слоя. Для краткости эти множества входов и выходов будем называть векторами. При обучении предполагается, что для каждого входного вектора существует парный ему целевой вектор, задающий требуемый выход. Эти векторы называются обучающей парой. Сеть обучается на многих парах. Перед обучением синаптические веса инициализируются случайными числами в диапазоне от 0 до 0,1. Процесс обучения состоит в вычислении выходного вектора сети и коррекции весовых матриц для каждой обучающей пары на каждой итерации по приведенным ниже формулам [6].

Формула коррекции весов для выходного слоя имеет вид

Wp-k (i + 1) = Wp-k (i) + n^kOUTp, где i — номер текущей итерации обучения; 5k = OUTk(1 — OUTk)(Tk — OUTk); wp-k — величина синаптического веса, соединяющего нейрон p скрытого слоя с нейроном k выходного слоя; η — коэффициент “скорости обучения”, позволяющий управлять средней величиной изменения весов; OUTp — выход нейрона p скрытого слоя; Tk — целевое значение выхода нейрона k выходного слоя; OUTk — выход нейрона k выходного слоя.

Формула коррекции весов для скрытого слоя записывается в виде

W p - q ( i + 1) = W p - q ( i ) + n5 q OUT p ,

N где i — номер текущей итерации обучения; 5q = OUTq(1 — OUTq) У^ 5kwq-k; wp-q — величина k =1

синаптического веса, соединяющего нейрон p предыдущего (в данном случае входного) слоя с нейроном q скрытого слоя; η — коэффициент “скорости обучения”, позволяющий управлять средней величиной изменения весов; OUT p — выход нейрона p предыдущего (в данном случае входного) слоя; OUT q — выход нейрона q скрытого слоя; N — количество нейронов последующего (в данном случае выходного) слоя.

Итерация включает перебор всех обучающих пар и суммирование среднеквадратичных ошибок прогнозов по всем выходам сети всех обучающих пар E ( i ). Процесс обучения заканчивается, когда разность суммарных ошибок текущей и предыдущей итераций E ( i ) —E ( i — 1) меньше заданного порога.

Модификация модели. В данной работе предлагается модель, состоящая из двух аналогичных персептронов, один из которых применим для прогнозирования почасового профиля нагрузки рабочего дня, другой — выходного или праздничного дня. В предлагаемой модели процессы обучения для рабочих и выходных (либо праздничных) дней были разделены, т. е. вычислялись четыре матрицы синаптических весов (по две для каждого персептрона). При обучении одной нейронной сети выбирались фактические данные только рабочих дней, и полученные весовые матрицы использовались только при прогнозировании профиля нагрузки рабочих дней. Вторая нейронная сеть использовалась для прогнозирования профиля нагрузки выходных (либо праздничных) дней.

В рассматриваемом случае выходной слой, представляющий собой почасовой профиль нагрузки за сутки, содержит 24 нейрона, скрытый слой — 15 нейронов, а входной — 30 нейронов.

Входной вектор содержит характеристики потребления электроэнергии за предыдущие сутки (3 нейрона), среднесуточные температуры воздуха предыдущего дня и прогноза температуры воздуха прогнозируемого дня (2 нейрона). При обучении персептрона в качестве прогноза температуры использовалась известная фактическая температура. Для учета сезонности используется 12 нейронов по количеству месяцев в году и три по количеству декад в месяце, а для учета типа суток — 10 нейронов (семь дней недели, праздничные, предпраздничные и послепраздничные дни). На три из этих входов, соответствующих месяцу, декаде в месяце и типу прогнозируемых суток, подается число 10, на остальные входы — число 1.

На входы трех нейронов, отражающих характер сложившегося потребления электроэнергии, подаются величины суточного расхода электроэнергии за предыдущие сутки, а также величина максимального и минимального часовых расходов за предыдущие сутки, при расчете которых учитывается, является ли прогнозируемый день рабочим или выходным (либо праздничным) днем.

Процесс обучения каждой сети включает два этапа. Сначала сеть обучается на всем задаваемом множестве обучающих пар (временной интервал до 1,5 лет в зависимости от имеющихся в базе фактических данных), а затем дообучается на минимальном временном интервале (месяц, предшествующий прогнозируемому дню). Обучающей парой являются входной вектор и целевой вектор (известный фактический почасовой профиль нагрузок для дня, представленного входным вектором). Значения входного и целевого векторов нормализуются, т. е. преобразуются в относительные величины в диапазоне от 0 до 1.

Точность прогноза, основанного на применении методов искусственного интеллекта, зависит от имеющихся исходных данных, определяющих архитектуру сети, степени достоверности данных и требуемого периода прогнозирования. Для краткосрочного прогнозирования нагрузки предприятия необходимыми исходными данными являются данные статистической отчетности по суточному электропотреблению. Для высокой достоверности используемых данных на исследуемом предприятии изначально должна быть внедрена высокоточная многофункциональная автоматизированная система контроля и учета потребления. Такая система создана в 2005 г. в Новосибирском научном центре в рамках программы “Энергосбережение СО РАН” [2, 7]. Система содержит центральный сервер с интегрированной базой данных и 26 периферийных центров сбора данных со своими локальными базами данных в институтах центра. Важным результатом создания этой системы является получение большого массива достаточно подробной информации о потоках различных энергоресурсов и технологических параметрах этих ресурсов.

Некоторые результаты обработки реальных данных электропотребления из базы одного из институтов СО РАН приведены ниже. Представлены результаты прогноза, полученные с использованием описанной в настоящей работе модели, для трех случаев:

• —    почасовые расходы на малом интервале (одни сутки);

• —    почасовые расходы на 20-суточном интервале;

• —    суточные нагрузки за две декады.

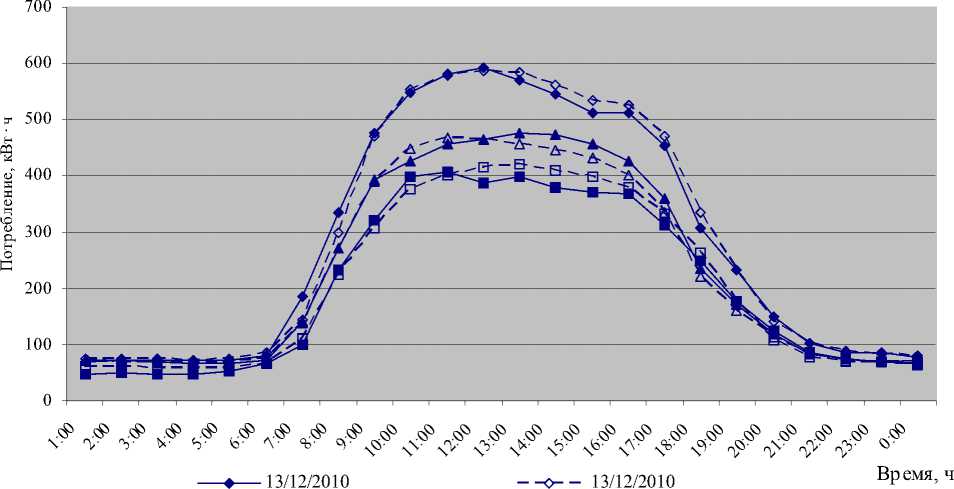
На рис. 2 приведены почасовые профили фактической нагрузки и графики прогноза потребления активной электроэнергии одним из академических институтов СО РАН в различные рабочие дни:

11 октября 2010 г. — осень (среднесуточная температура наружного воздуха +8,4 ˚С), понедельник, максимальное абсолютное значение доверительного интервала — 0,54 кВт · ч, минимальное — 0,02 кВт · ч, средняя погрешность прогноза — 3,07 %;

• 1 апреля 2011 г. — весна (среднесуточная температура наружного воздуха +2,5 ˚С), пятница, максимальное абсолютное значение доверительного интервала — 0,12 кВт · ч, минимальное — 0,01 кВт · ч, средняя погрешность прогноза — 1,8 %;

• 13 декабря 2010 г. — зима (среднесуточная температура наружного воздуха - 24 ˚С), понедельник, максимальное абсолютное значение доверительного интервала — 0,28 кВт · ч, минимальное — 0,03 кВт · ч, средняя погрешность прогноза — 1,7 %.

01/04/2011                              01/04/2011

11/10/2010                              11/10/2010

Рис. 2. Почасовые профили фактической нагрузки и графики прогноза потребления активной электроэнергии одним из академических институтов СО РАН в различные рабочие дни: темные точки — фактическая нагрузка; светлые — прогнозируемая нагрузка

Значения доверительных интервалов вычислялись по выборке из 100 элементов.

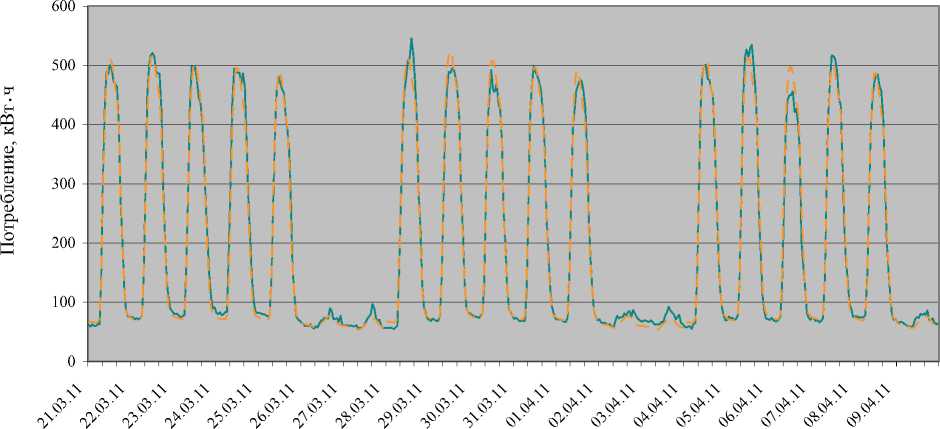
На рис. 3 представлены почасовые профили фактической и прогнозируемой нагрузок потребления активной электроэнергии одним из академических институтов СО РАН за две декады (третья декада марта и первая декада апреля). Максимальное абсолютное

Время, ч

Рис. 3. Почасовые профили фактической и прогнозируемой нагрузок потребления активной электроэнергии одним из академических институтов СО РАН за две декады (третья декада марта и первая декада апреля): сплошная линия — фактическая нагрузка; штриховая — прогнозируемая нагрузка

Значения средней относительной погрешности суточных прогнозов

Дата Средняя относительная погрешность прогноза за сутки 21.03.2011, понедельник 1,56 22.03.2011, вторник 1,99 23.03.2011, среда 2,17 24.03.2011, четверг 3,28 25.03.2011, пятница 1,58 26.03.2011, суббота 0,77 27.03.2011, воскресенье 0,82 28.03.2011, понедельник 2,93 29.03.2011, вторник 1,65 30.03.2011, среда 1,68 31.03.2011, четверг 1,31 01.04.2011, пятница 1,96 02.04.2011, суббота 1,30 03.04.2011, воскресенье 1,86 04.04.2011, понедельник 1,31 05.04.2011, вторник 2,41 06.04.2011, среда 3,32 07.04.2011, четверг 1,72 08.04.2011, пятница 1,57 09.04.2011, суббота 0,87 значение доверительного интервала составило 0,27 кВт·ч, минимальное — 0,01 кВт·ч, средняя погрешность почасового прогноза — 1,87 %. Значения средней относительной погрешности суточных прогнозов приведены в таблице.

На рис. 4 приведены профили суточной фактической и прогнозируемой нагрузок потребления активной электроэнергии за две декады апреля. Средняя погрешность прогноза — 0,65 %.

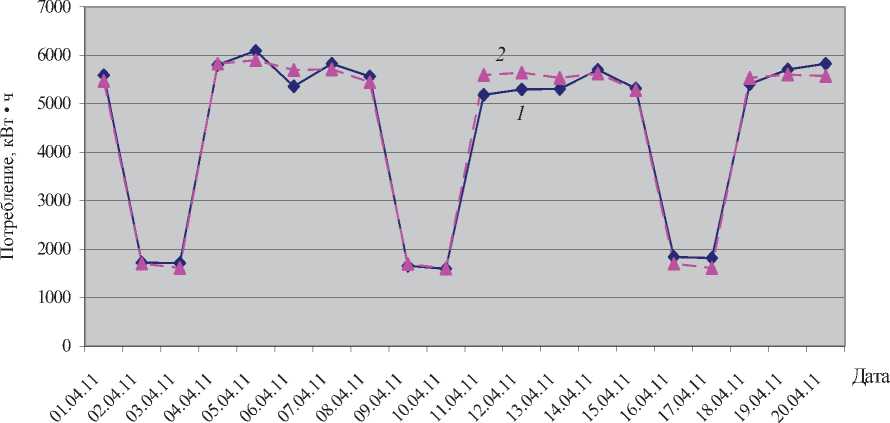
Рис. 4. Профили суточной фактической и прогнозируемой нагрузок потребления активной электроэнергии за две декады апреля:

1 — фактическая нагрузка; 2 — прогнозируемая нагрузка

Полученные результаты свидетельствуют о возможности использования предлагаемого подхода для прогнозирования электрической нагрузки. Нейронные сети являются подходящим инструментом для решения задач прогнозирования энергопотребления, альтернативным традиционным статистическим методам. Дальнейшее повышение точности прогноза возможно за счет более точной и тонкой настройки структуры сети и изменения количества входных параметров.