Прогноз срока службы оптического кабеля линии связи с учетом изменений температуры окружающей среды и остаточных деформаций модульных трубок

Срок службы оптического кабеля (ОК) линии передачи определяется сроком службы оптических волокон (ОВ) в его конструкции в условиях эксплуатации. В свою очередь, срок службы ОВ во многом определяется процессами усталостного разрушения и существенно зависит от приложенной к нему нагрузки [1-8], которая зависит от конструкции кабеля и внешних условий, в частности, температуры окружающей среды. При низких отрицательных температурах напряжения в волокнах кабеля возрастают.

При строительстве линий передачи оптический кабель в процессе прокладки и монтажа подвергается внешним механическим воздействиям, степень которых зависит от применяемых технологий и функционирования системы качества строительной организации, в том числе от подготовки специалистов и соблюдения технологической дисциплины.

Человеческий фактор создает предпосылки вероятности того, что по завершении строительства могут иметь место остаточные деформации элементов конструкции ОК, в частности модульных трубок. Такие деформации создают условия для увеличения напряжения в волокнах кабеля.

В статье предложен алгоритм прогноза срока службы ОВ в ОК линии передачи, позволяющий учитывать колебания температуры окружающей среды, и получены оценки снижения срока службы ОК в процессе его эксплуатации в результате действия низких отрицательных температур при наличии остаточных деформаций модульных трубок.

Модель и алгоритм прогноза срока службы оптического кабеля с учетом изменений приложенной к ОВ нагрузки

В основе методов прогноза срока службы ОВ лежат статические модели механических напряжений в стекле и кинетические модели роста дефектов. В [1] в общей форме были представлены три типа моделей вида, описывающих рост дефектов кварцевого стекла оптических волокон: модель усталостного механического разрушения (тип 1), описывающая рост дефекта в одной стадии, модель коррозионного разрушения (тип 2) и гидролитическая модель роста дефектов кварцевых оптических волокон (тип 3). В работах [1-4] показано, что для долгосрочных прогнозов первый тип модели дает наиболее оптимистичную картину и отличается наибольшей погрешностью. Вместе с тем в последние годы в задачах прогноза показателей надежности ОВ, и в частности оценивания их по результатам перемотки ОВ под нагрузкой, используют механическую модель, описывающую рост дефекта в две стадии [5-9]. Экспериментальные исследования подтвердили ее адекватность [5; 7-8], что и определило ее широкое применение.

При выборе модели роста дефектов будем исходить из следующих положений. Во-первых, будем полагать, что в процессе эксплуатации волоконно-оптической линии передачи (ВОЛП) на ОК и ОВ в нем действуют только статические нагрузки. Разобьем весь исследуемый период службы ОК на интервалы времени, в течение которых нагрузку на ОВ можно считать постоянной. Это позволяет на каждом отдельном интервале времени применить двухстадийную механическую модель и воспользоваться для описания остаточных напряжений в оптическом волокне известным выражением [4; 7-8]:

^zVmax) ^/UmiJ------^z ’    0)

'i-\^Qj^l^r, где Bi – константа, учитывающая параметры статической усталости волокна для соответствующих условий окружающей среды, коэффициент интенсивности напряжений и геометрию дефекта на i-ой стадии; Nt – параметр статической усталости кварцевого ОВ на i-ой стадии; ^ “j – нагрузка, приложенная к оптическому волокну, на jом интервале времени; о ^- прочность ОВ на момент времени t на j-ом интервале времени. Ти- пичные значения параметров кварцевых ОВ сведены в таблицу 1 [4; 8].

Таблица 1. Значения параметров кварцевых ОВ

№	Параметр	Значение
I	Уровень напряжений при испытаниях на разрыв, ГПа	0,7
2	Пределы изменений N]	18-25
3	Среднее значение N]	21
4	Среднее значение N2	4,5
5	Г	0,645
6	В! , ГПа2 С	4,5x10"5
7	В2, ГПа2 С	0,0082

Задавая исходную (инертную) прочность ОВ, вектора ^ aj ’ ^min j ^ ^max j , рассчитываем прочность ОВ в конце каждого интервала времени. Полагаем, что ОВ разрушено при условии [11]:

°№°aJ-

Таким образом, на основе итерационного подхода определяем ожидаемый срок службы ОВ.

Моделирование нагрузки, приложенной к ОВ в ОК модульной конструкции в процессе эксплуатации ВОЛП

Известно [9], что ОВ в модулях оптического кабеля расположено по геликоиде, и его радиус кривизны определяется минимальным диаметром модульной трубки и разностью длин ОВ и модуля. Изогнутое ОВ находится под напряжением. Механическую нагрузку на поверхности изогнутого кварцевого волокна можно рассчитать по формуле [10]

°"o-E_o (1 + 2,875 z) z,

где Z = b/^R + /> + /?) – деформация растяжения наружного слоя кварцевого волокна; 7T₀ – величина модуля упругости кварцевого стекла при z —> o, равная 7,4 ГПа; R – радиус изгиба волокна; b – радиус волокна; h – толщина защитного покрытия.

Более широко известно ее приближение для больших значений радиусов изгиба [11]:

<70 = —--.

° R

Для определения среднего значения радиуса изгиба ОВ в модулях ОК воспользуемся резуль- татами [12-13]. В первом приближении эту величину можно оценить как R « d„ /(2<8) [13] или R « d„ /(ЗЯ) [14], где ^ m – внутренний диаметр модульной трубки, а 51 – оценка относительного удлинения ОВ.

Для определения более корректных оценок воспользуемся формулой [13]

1 -cos(

где угол Ф определяется при решении уравнения

1-2 sin((9/2)/ ф = 51. (4)

Оценка относительного удлинения из-за изменения температуры рассчитывается по формуле [9; 12-13]:

&_T =^a-^T, (5)

где 5a, = (a_T -a_OB) – разность температурных коэффициентов линейного расширения материала модульной трубки a_T и ОВ ^аов ’ AT' = (j⁷ — T_o ) – разность между текущим значением температуры T и некоторым условным значением температуры T ₀ , при которой длина ОВ равнялась бы длине модульной трубки.

Согласно [12], при нормальной температуре среднее значение относительного удлинения равно

6l₀=Q.57i'd'-!p-, (6) где б/д – диаметр модульной трубки по техническим условиям; p – среднее значение шага геликоиды волокна в модульной трубке. Статистические исследования показали, что это значение лежит в пределах 20…100 мм [12].

Соответственно, результирующее значение при температуре T определяется как сумма:

51 = а₀ + 51 _т. (7)

Если в результате внешних механических воздействий на ОК он был деформирован, а по завершении воздействий имеют место остаточные деформации модульных трубок, то при оценивании напряжений ОВ в модуле при изменении температуры минимальный диаметр модульной трубки (3) определяется приближенно как разность исходного диаметра модульной трубки по техническим условиям б/о и ее остаточной деформации А , то есть ^m ^0 ^ m ^.

На графике (см. рис.1) представлены оценки напряжений на поверхности оптического волокна в зависимости от температуры окружающей среды и остаточной деформации модульных трубок из полибутилентерефталата с внешним диаметром 2,0 мм.

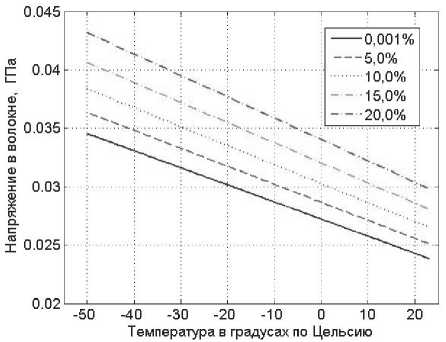
Рис. 1. Зависимости напряжений в ОВ от температуры окружающей среды и остаточных деформаций модуля ОК

Исследование срока службы ОК ВОЛП, введенной в эксплуатацию, с учетом остаточных деформаций модулей и температуры окружающей среды

Описанный алгоритм позволяет строить имитационные модели, учитывающие архивные данные среднемесячных температур в районе, где предполагается прокладка кабеля. В данной работе в целях исследования влияния низких отрицательных температур в сочетании с деформациями модулей на срок службы ОК в условиях эксплуатации полагали, что в зимний период температура постоянна и равна некоторому значению, для которого и выполнялся расчет.

Результаты вычислений представлены на рис. 2. На рис. 2а представлены результаты расчетов для гипотетического примера в предположении, что исходная (инертная) прочность ОВ соответствует уровень напряжений при испытаниях его на разрыв. Конечно же, это маловероятно, тем более если кабель подвергался воздействиям, которые привели к деформациям модульных трубок. На рис. 2б и рис. 2в представлены результаты прогнозов для случаев, когда при изготовлении ОК и в процессе строительства инертная прочность ОВ снижается на 20% и на 30%, соответственно.

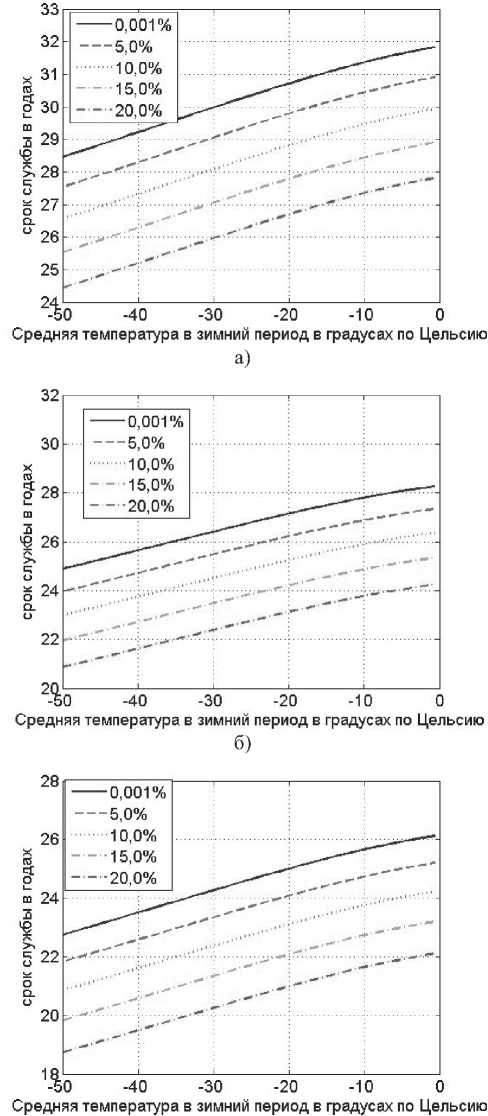
в)

Рис. 2. Зависимость срока службы от средней температуры

В первом случае срок службы кабеля менее 25 лет имеет место только при средней температуре в зимний период ниже минус 50о С и деформациях модуля более 15%. При снижении исходной прочности ОВ на 20% срок службы кабеля менее 25 лет прогнозируется уже при средней температуре в зимний период ниже минус 30о и деформациях более 5%. При деформациях более 10% срок службы ОК менее 25 лет для всех отрицательных значений средней температуры в зимний период. При снижении исходной прочности на 30% даже незначительные деформации модуля приводят к сокращению срока службы кабеля до 25 лет и менее для всех отрицательных значений температуры в зимний период. А при средних значениях температуры зимой ниже минус 20оС прогнозируемый срок службы не превышает 25 лет даже для кабеля с недеформированными модулями.

В целом, следует отметить, что деформации модуля до 20% сокращают срок службы кабеля до четырех лет, и эта величина практически не зависит от исходной прочности ОВ и температуры, при которой эксплуатируется ОК. Результаты моделирования подтвердили, что одним из наиболее существенных факторов, определяющих срок службы ОК, является исходная прочность ОВ.

Заключение

В работе предложена модель прогноза срока службы ОК ВОЛП, введенной в эксплуатацию, с учетом остаточных деформаций модулей и температуры окружающей среды. Получены оценки срока службы ОК в зависимости от средней температуры в зимний период и степени деформации оптических модулей. Показано, что сокращение срока службы кабеля вследствие деформации модуля практически не зависит от исходной прочности ОВ и температуры, при которой эксплуатируется кабель. При этом срок службы ОК снижается с понижением температуры в зимний период. В результате моделирования подтверждено, что одним из наиболее существенных факторов, определяющих срок службы ОК, является исходная прочность ОВ. Показано, что при внешних воздействиях на ОК в процессе строительства и монтажа, приводящих к деформациям модулей и снижению инертной прочности ОВ, даже незначительные деформации модульных трубок могут привести к существенному сокращению срока службы ОК, эксплуатируемых в зимний период при температурах ниже минус 30оС.