Прогнозирование аэродинамических нагрузок и аэроупругих реакций при решении задач динамической аэроупругости

В последние годы наблюдается значительный прогресс в разработке компактных моделей для трансзвуковой аэродинамики и аэроупругости [1–3], которые учитывают нелинейные характеристики при ограниченном числе степеней свободы. Этот прогресс основан на новых методах математического моделирования и разработке специализированного программного обеспечения.

Высокоточные методы вычислительной гидродинамики (далее – CFD) [4–6], традиционно используемые для прогнозирования динамики нестационарного потока, неэффективны для оценки аэроупругой устойчивости. Это обусловлено значительными вычислительными затратами, связанными с методом Вольтерра – Винера, лежащим в основе CFD-методов.

Для решения этой проблемы разрабатываются модели нестационарного течения с пониженным порядком, основанные на методе Вольтерра – Винера – Ганди. Эти модели требуют менее интенсивных вычислений и могут быть реализованы с помощью специализированного программного обеспечения.

Существуют два основных подхода:

• 1)    методы выделения признаков [7–11]. Эти методы снижают сложность системы и вычислительные затраты путем проецирования многомерных данных о потоке на множество базисов низкого порядка. Они требуют разработки новых алгоритмов и программ-

• ного обеспечения для эффективной обработки больших наборов данных и выполнения соответствующих математических операций;

• 2)    методы идентификации системы . Эти методы описывают систему с помощью краткого математического выражения «черного ящика». Разработка таких моделей требует применения специализированных методов идентификации систем и создания соответствующего программного обеспечения.

Нестационарные аэродинамические модели пониженного порядка (далее – МПП) широко применяются в аэроупругости [12; 13], где возникают нелинейности из-за аэродинамических сил, колебаний конструкции и других факторов.

В данной работе предлагается нестационарная аэродинамическая модель на основе сети сверточных длинно-коротких связей (далее – СДКП), способная работать с переменными числами Маха. Модель отличается от предыдущих тем, что может обрабатывать большое количество обучающих выборок и прогнозировать нагрузки в широком диапазоне чисел Маха.

Разработанная модель СДКП представляет собой перспективный инструмент для аэродинамического и аэроупругого анализа, способный улучшить процесс проектирования авиационных конструкций и повысить их надежность.

Обучение усовершенствованной архитектуры сети СДКП

Усовершенствованная архитектура сети СДКП, способная обрабатывать и генерировать последовательности данных, привела к значительному прогрессу в вычислительной аэроупругости. Способность сети обрабатывать большие массивы данных и прогнозировать нагрузки в различных условиях представляет собой существенное достижение.

Сеть СДКП обеспечивает непрерывный процесс обучения, связывая выходные данные с предыдущими и текущими входными данными на каждом временном шаге. Блок памяти СДКП позволяет моделировать сложные аэроупругие явления, инкапсулируя динамику входа-выхода во времени. Включение элементов входа, выхода и забывания позволяет сети обрабатывать временные зависимости и нелинейности, что повышает точность и надежность аэроупругих прогнозов.

Методология вычислительной оптимизации, использующая структуру сети СДКП и стратегическое использование входных, выходных и забывающих элементов в сочетании с обучением с помощью Keras в Python, знаменует продвижение в вычислительной аэроупругости.

Нестационарное аэродинамическое моделирование

В исследовании представлена модель уменьшенного порядка (далее – МПП) для нестационарной аэродинамики, основанная на сети глубокого обучения. Модель использует три набора данных: обучающий, проверочный и тестовый [14]. Обучающий набор используется для определения параметров модели, проверочный – для оценки эффективности модели во время обучения [15; 16], а тестовый – для оценки производительности модели на реальных данных.

Процесс построения модели МПП с использованием сети СДКП включает следующие этапы:

• 1)    сбор обучающих данных при заданных числах Маха с помощью моделирования IOP;

• 2)    валидация – вычисление проверочных данных с малой амплитудой для оценки способности модели к обобщению;

Прогнозирование аэродинамических нагрузок и аэроупругих реакций при решении задач ...

• 3)    обучение модели СДКП с использованием обучающих и валидационных данных;

• 4)    замена сети СДКП вместо модели IOP после обучения для дальнейшего анализа (тестовый случай).

Сеть СДКП позволяет получить более точные и надежные расчеты устойчивости в авиационной технике, учитывая нелинейные взаимодействия между входными и выходными данными. Модель может быть как интегрирована с уравнениями движения конструкции для аэроупругого анализа, так и использована в аэродинамическом моделировании без связи со структурой. Интеграция модели с конструктивными уравнениями движения повышает точность аэроупругого анализа, расширяя возможности современной авиационной техники.

Метод временного перемещения аэроупругих систем. Потоковый решатель

В настоящем исследовании используется решатель нестационарного течения, основанный как на уравнениях Эйлера, так и на уравнениях Навье – Стокса со средним значением по Рейнольдсу. Для текущего исследования используется решатель Эйлера. Для пространственной дискретизации применяется вычисление конечного объема с центрированием по ячейкам с использованием схемы разности центров, управляющие уравнения безразмерны по средней аэродинамической хорде c , скорости звука a _∞ и температуре свободного потока T _∞. Более подробную информацию о численных методах можно найти в [16]. В данной работе используется алгоритм динамически деформируемой сетки, основанный на интерполяции RBF [17]. CFD-решатель был протестирован в некоторых случаях, таких как явление флаттера или буфета [14; 16].

Структурные уравнения движения

Типичная двумерная аэроупругая модель с двумя степенями свободы при погружении и тангаже показана на Рисунке 1.

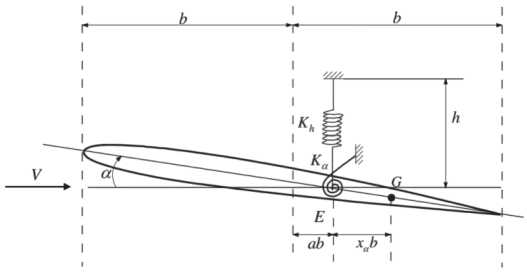
Рисунок 1. Аэроупругая модель с двумя степенями свободы Источник: здесь и далее рисунки выполнены авторами .

Следующее уравнение является структурным уравнением движения:

I 0 ^ a )

a

a

xa ra

h

\ b \ +

a

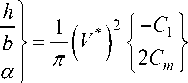
где h и α – смещение аэродинамического профиля при погружении и угол тангажа соответственно; Cl и Cm – соответственно, коэффициенты подъемной силы и тангажного момента; rα – радиус вращения аэродинамического профиля вокруг упругой оси; xa – статический дисбаланс профиля (безразмерное расстояние между центром тяжести и осью шарнира); wh и ωα – несвязанные собственные частоты падения и основного тона соответственно; V* – приведенная скорость, которая определяется как

V * = V / ( ^ a b ^ ) ,

^ =

m a

2 , P b где b, μ и V – длина половины хорды, массовое соотношение и скорость набегающего по- тока соответственно.

Уравнение (2) может быть записано в матричной форме как M g + K g = Q ,

где M , K , Q , ξ – обобщенные матрицы массы, жесткости, обобщенный вектор силы и вектор структурных координат соответственно.

После преобразования (3) в представление пространства состояний гибридный линейный многоступенчатый метод четвертого порядка точности [17] используется для решения уравнения аэроупругости во временной области, где применяется метод прогнозиста-корректора. В процедуре прогнозирования структурная и аэродинамическая части расширяются в четкой схеме, но на этапе коррекции в явной схеме расширяется только аэродинамическая часть, тогда как структурная часть расширяется в нечеткой схеме.

При использовании вышеупомянутого численного метода структурный отклик при заданном числе Маха и V ^* может быть решен во временной области. Аэродинамический временной шаг безразмерен:

DT = dt / 1 2 — I ,                                 (4)

\   ^ J где dt – физический временной шаг.

Результаты и обсуждение

В данном исследовании смоделирована нестационарная аэродинамика крыла NACA 64A010 в околозвуковом режиме с использованием нестационарного аэродинамического постоянного запоминающего устройства (далее – ПЗУ) и нелинейного аэроупругого моделирования. Модель СДКП с 32 модулями и одним скрытым слоем, дополненная LSTM-ячейками памяти и многослойными структурами, обученная с помощью оптимизатора Adam, прогнозирует аэродинамические нагрузки и анализирует тенденции LCO. Результаты подтверждают эффективность модели СДКП, открывая путь к улучшению проектирования авиационных конструкций и повышению их надежности.

Пример обучения и валидации

В исследовании изучается нестационарная аэродинамика в околозвуковом режиме с использованием трех чисел Маха: 0,74; 0,78 и 0,82. Выбор этого диапазона обусловлен сложностью моделирования в околозвуковом потоке, особенно в пределах изменения числа Маха на 0,08. Это дополнительно показано на Рисунке 2, где приведены контуры стационарного потока при Ma = 0,74, Ma = 0,78 и Ma = 0,82.

Прогнозирование аэродинамических нагрузок и аэроупругих реакций при решении задач ...

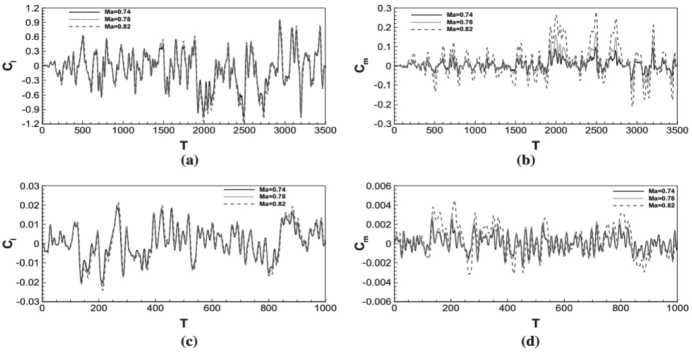
Рисунок 2. Аэродинамические нагрузки, рассчитанные на основе ВГД-моделирования при трех числах Маха: a – коэффициент подъемной силы тренировочного кейса; b – моментные коэффициенты обучающего случая; c – коэффициент подъема обучающего случая; d – моментные коэффициенты обучающего случая

Оно резко варьировалось для потока от минимальных до максимальных чисел Маха, демонстрируя избыточную величину выбранного диапазона чисел Маха для множественных нелинейных характеристик. Чтобы охватить широкие диапазоны амплитуды и частоты, сигналы возбуждения, используемые для обучения и проверки ПЗУ, сконструированы в виде двух сигналов с фильтрованным белым гауссовым шумом (далее – ФБГШ), которые включают 3500 и 1000 временных шагов при всех числах Маха соответственно, как показано на Рисунке 2. Для фиксации характеристик различных частот аэродинамический временной шаг DT устанавливается равным 0,6 и 0,4 для моделирования МПП и вычислительной гидродинамики. Предлагаемое МПП представляет собой систему MIMO, где входные и выходные векторы определяются как ut =

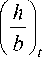
Ma

y t =[ ( C l ) t ( C m ) t ]

Динамические характеристики в выбранном диапазоне чисел Маха сравниваются на Рисунке 2. Для одного и того же типа движения наблюдается большая разница в аэродинамической характеристике во всем диапазоне тренировочных чисел Маха.

Для обучения модели используется метод уменьшения градиента, поэтому для анализа неопределенности сети СДКП путем десятикратного обучения модели получают десять различных моделей СДКП и сравнивают их друг с другом.

Для проверки работоспособности модели используется случайное движение с двумя степенями свободы при Ma = 0,77, сравниваются результаты, полученные с помощью этих моделей СДКП и виртуального газодинамического моделирования (далее – ВГД). На Рисунке 3 показано сравнение между моделями ВГД и диапазоном ошибок по результатам этих моделей. Выходные данные модели незначительно различаются при различных начальных условиях обучения, что подтверждается сравнением относительной погрешности каждой модели в прогнозировании случайных движений при четырех различных числах Маха (см. Рисунок 4).

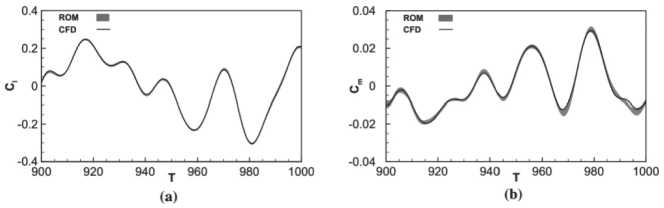
Рисунок 3. Сравнение аэродинамических нагрузок для случайного движения при Ma = 0,77 между моделями ВГД и диапазоном ошибок по результатам десяти моделей: а – коэффициент подъемной силы; b – коэффициент момента

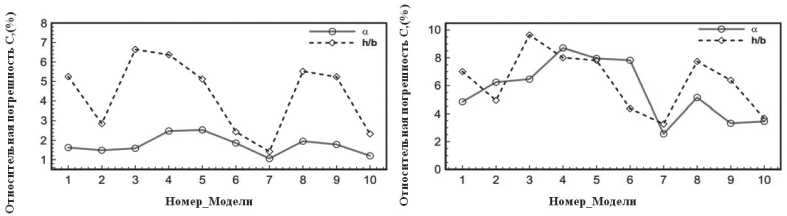
Рисунок 4. Средняя относительная погрешность аэродинамических нагрузок для случайных движений при Ma = 0,75; 0,77; 0,79 и 0,81: а – коэффициент подъемной силы; b – коэффициент момента

Выбранные числа Маха для оценки модели отличаются от значений для обучения модели. Относительная погрешность, используемая для оценки модели, определяется как

RE ₌ I ^у мпп ^у вгд I ^F . _100%,                          (6)

I Увгд IF где результат МПП представлен yМПП, в то время как yВГД обозначает результат, полученный в результате моделирования ВГД.

На Рисунках 3 и 4 наблюдается расхождение между этими моделями, указывающее на устойчивость предложенной модели к начальным условиям обучения.

Заключение

В исследовании представлена модель уменьшенного порядка для нестационарной аэродинамики, основанная на глубоком обучении, которая эффективно прогнозирует аэродинамические нагрузки и аэроупругие реакции при различных числах Маха. Модель использует сеть долговременной памяти (LSTM) и отработана на трансзвуковом профиле с двумя степенями свободы. МПП точна как для линейных, так и для нелинейных аэродинамических характеристик. Использование глубокого обучения для обработки больших объемов данных позволяет оптимизировать процесс проектирования и снизить трудозатраты в современном авиастроении.

Прогнозирование аэродинамических нагрузок и аэроупругих реакций при решении задач ...