Прогнозирование цен на меховые женские головные уборы в РФ

Даннаястатья посвящена анализу средних потребительских цен на женскиеголовные уборыиз натурального меха в РФ запериод сянваря 2013 по декабрь 2016, а также прогнозированию значений цены за январь и февраль 2017 года. Данный показатель является, во-первых, явно сезонным, а, во-вторых, актуаленпо причинеинтереса малого бизнеса и производителей меховых изделий, которые должны быть осведомлены о ценовом сегменте продаж женских головных уборов из натурального меха. Цены на данный товар интересны и потребителям (жителям Сибири и Севера).

Целью  работы является: построение модели, наиболее точно отражающей исходный временной ряд X(t), прогнозирование его будущих значений на основе построенной адаптивной модели Брауна и эконометрической модели ARMA, выбор наиболее адекватной из них.

Проанализировав структуру сезонных колебаний и заметив, что их амплитуда в течение всего периода исследования остается относительно одинаковой, мы можем сделать вывод о том, что наш временной ряд имеет аддитивную сезонность и в результате состоит из следующих трех составляющих: тренд-циклической компоненты, аддитивной сезонной компонентыи случайной составляющей.

Сезонные индексы лишний раз подтверждают наш вывод о характере сезонности. Максимальный прирост цен наблюдается в январе, затем происходит снижение прироста относительно тренда до августа, где наблюдается минимальное значение сезонного индекса.

После очищения ряда X(t) от сезонности мы получили ряд TRC с тренд-циклической составляющей и случайной компонентой.

Колебания ряда TRC связаны с наличием циклической и случайной компонент, а монотонное возрастание – с наличием линейного тренда. Этот ряд по сравнению с рядом X(t) более четко отражает изменение цены, не связанное с сезонностью. В результате можно заметить резкое прекращение монотонного возрастания ряда TRC с октября по декабрь 2016 года, что говорит о снижении значений цены на женские меховые головные уборы из натурального меха (рис. 1). На снижение этого показателя в октябре главным образом повлияла борьба с контрафактными товарами посредством электронной маркировки меховых изделий (чипирования). Именно в октябре цены на меховые изделия снизились в два раза из-за проверок Роспотребнадзора, связанных с введением электронной маркировки меховых изделий.Всего по итогам проверки было арестовано более 1000 меховых изделий на 40,1 млн рублей [4]. Член правления РСПП РФ Андрей Разбродин объясняет причины снижения цен желанием как можно скорее реализовать нечипированную продукцию.

Перейдем непосредственно к построению адаптивной модели Брауна. В результате проведенных расчетов мы определили оптимальные значения параметров модели:α (параметр адаптации) = 0,47, при этом значении наблюдается минимальное значение величины ошибки аппроксимации;а (48) = 8088,569;b (48) = –57,920.Ошибка аппроксимации для контрольной выборки составила 1,896%.

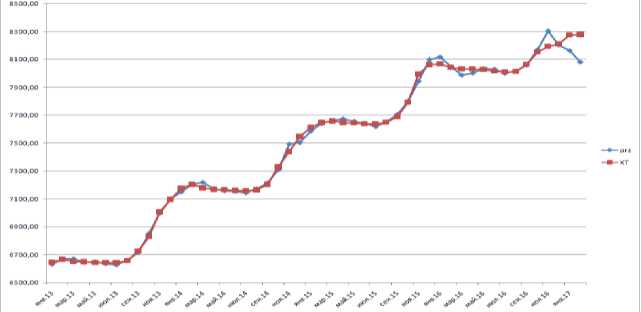
Рис. 1. – График исходного (красный) и прогнозного (синий) рядов.

В целом оба ряда близки по значениям друг другу, что говорит о хорошем качестве построенной модели. Это также подтверждается средней ошибкой равной 0,236. Помимо этого метод Брауна пригоден для прогнозирования (средняя ошибка 1,896%  <10%). Однако если ориентироваться по направлению прогноза (январь и февраль 2017 год), то уровень цен имеет тенденцию к снижению, а на практике, наоборот, цены возрастают. Данное поведение цен можно объяснить повышением себестоимости меховых изделий в связи маркировкой (чипированием) меховых изделий.

Теперь перейдем к процессу построения эконометрической модели с помощью статистического пакета EViews.

Вначале исходный ряд X(t) представлял собой вид (1):

Xt = TRC + ses_a,                        (1)

где ses_a – аддитивная сезонная составляющая, а TRC состоит из линейного тренда и случайной составляющей (остатка).

Тесты Дарбина-Уотсона и Уайта выявили гетероскедастичность и автокорреляцию. Это позволило нам сделать вывод о несостоятельности и неэффективности оценок параметров модели и их непригодности для дальнейшего использования.

Наличие единичных корней было проверено с помощью теста Филлипса–Перрона. По результатам теста исходный временной ряд является нестационарным (наблюдаемые значения были больше критических) и,соответственно, имеет тренд. Так как временной ряд стационарен относительно этого тренда, то можно сказать, что ряд X(t) является TS-рядом. Единичные корни присутствуют, порядок интегрирования – 1.

В результатеанализа коррелограммы выделенного тренда (рис. 4) мы обратили внимание на характер ряда PACF, который показывает выраженную авторегрессию первого порядка ar(1) .

После выделения авторегрессии первого порядка из остатков они стали белым шумом (что говорит об отсутствии в них автокорреляции, ARCH– компоненты, а также постоянстве дисперсии)

После включения ar(1) в модель ARMA мы получилиМАРЕ- оценки, что говорит о качестве идентифицируемой нами моделиARMA.

Окончательный вид модели ARMA (2):

Xt = a+ bt + α1*x(t-1) + e(t) + ses_a, (2)

где a+bt - линейный тренд; a1*x(t-1) + e(t) - авторегрессия первого порядка; ses_a - аддитивные сезонные индексы. Ошибка аппроксимации получившейся эконометрической модели равна 0,54 %.

Сам график исходного ряда и получившейся модели представлен на рис. 2.

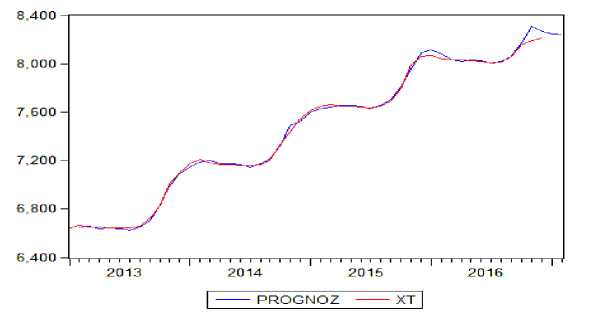
Рис. 2. – Исходный временной ряд и модель ARMAс прогнозными значениями.

В результате исследования мысравнилидве моделиизаметили, что лучшая из них – эконометрическая. Это подтверждается большим характером её универсальности и меньшей ошибкой аппроксимации.