Прогнозирование цен на вторичном рынке жилья Санкт-Петербурга

С момента появления в России рынка жилой недвижимости возникла потребность в учете и прогнозировании его развития. За четверть века существования рынка жилья исследователи (например, Стер-ник Г.М., Стерник С.Г., Дробышевский С.М., Снитюк В.Е., Печенкина А.В. и др.) построили множество моделей для прогноза динамики его характеристик. В работе [1] рассмотрена эволюцию моделирования российского рынка жилья, рассмотренные модели показали хорошую точность прогноза в краткосрочном периоде, в среднесрочном периоде прогноз не всегда оказывался адекватным. Отчасти это связано с тем, что дополнительно возникает необходимость прогнозировать каждый фактор, включенный в модель. В статье рассматривается прогнозирование на основе изолированного динамического ряда. В качестве прогнозируемого показателя рассмотрена средняя цена 1 кв. м жилья в г. Санкт-Петербург по данным сайта недвижимости BN.ru [2].

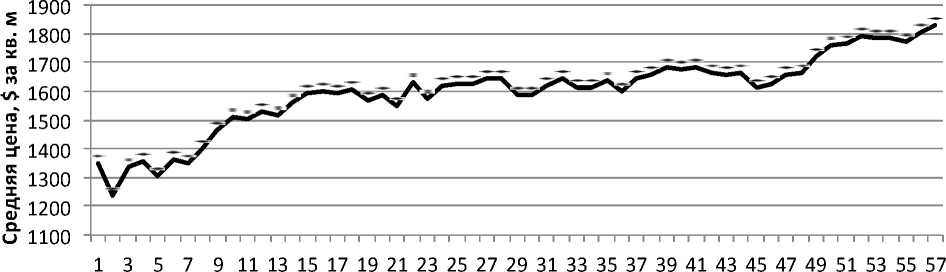
На рис. 1 представлена динамика средней цены предложения жилья на вторичном рынке по недельным данным за период с 15 января 1999 г. по 17 февраля 2017 г. в долларах США. Динамика цен за рассматриваемый период характеризуется изменчивой тенденцией. Попытка построения прогноза с учетом данных за весь представленный период не позволила подобрать адекватную модель. Период с 1999 г. по август 2008 г. характеризовался ростом цен по экспоненциальному тренду с коэффициентом детерминации 0,93. Цена за этот период выросла в 8,5 раза и составила 4500 долларов США/кв. м.

ГРНТИ 06.35.33

Марина Владимировна Боченина – кандидат экономических наук, доцент, доцент кафедры статистики и эконометрики Санкт-Петербургского государственного экономического университета.

t , неделя

Рис. 1. Средняя цена предложения на вторичном рынке жилья г. Санкт-Петербурга с января 1999 г. по февраль 2017 г., долл. США / кв. м [2]

Затем, до февраля 2009 г., наблюдался спад, характеризующийся линейной тенденцией с коэффициентом детерминации 0,91. За этот период цена упала на 48%. С февраля 2009 г. по февраль 2017 г. наблюдалась изменчивая тенденция. Функция автоматического подбора модели временного ряда в среде R ( auto.arima ) описывает этот период авторегрессионным процессом ( AR ) 4 порядка и один раз проинтегрированным ( I ) скользящим средним ( MA ) 3 порядка – ARIMA (4,1,3). Однако, описание экономических процессов столь сложными моделями, с множественными коэффициентами AR и MA одновременно, приводит к неочевидности влияния фактора [3]. В этом случае желательно подобрать модель, имеющую в своем составе не более одного процесса AR или MA (см. табл. 1).

Таблица 1

Модели средней цены предложения на вторичном рынке жилья г. Санкт-Петербурга, 2009-2017 гг., долл. США / кв. м

№	Модель	AIC	BIC	p-value
1	ARIMA (4,1,0)	4401,01	4421,10	0,058
2	ARIMA (4,1,1)	4398,94	4423,05	0,112
3	ARIMA (4,0,1)	4415,62	4443,77	0,107
4	ARIMA (4,0,0)	4417,95	4442.08	0,048
5	ARIMA (3,1,0)	4399,79	4415,86	0,091
6	ARIMA (3,1,1)	4398,03	4418,12	0,159
7	ARIMA (3,0,1)	4413,83	4437,95	0,235
8	ARIMA (3,0,0)	4417,24	4437,35	0,048
9	ARIMA (2,1,0)	4398,97	4411,02	0,090
10	ARIMA (2,1,1)	4396,20	4412,28	0,219
11	ARIMA (2,0,1)	4419,57	4439,68	0,016
12	ARIMA (2,0,0)	4418,73	4434,81	0,014
13	ARIMA (1,1,0)	4400,28	4408,31	0,034
14	ARIMA (1,1,1)	4401,80	4413,86	0,020
15	ARIMA (0,1,1)	4400,29	4408,32	0,034
16	ARIMA (1,1,2)	4395,91	4411,98	0,233
17	ARIMA (0,1,2)	4399,17	4411,22	0,084
18	ARIMA (1,1,3)	4402,50	4422,59	0,046
19	ARIMA (0,1,3)	4400,86	4416,93	0,065

С этой целью в среде R с помощью функции Arima были рассмотрены модели с различным составом AR и MA части. Все модели были исследованы на наличие автокорреляции в остатках с помощью критерия Бокса-Льюнга. В случае наличия автокорреляции в остатках критические значения вероятностей p-value, соответствующие значению статистики Бокса-Льюнга не превышают 0,05 (см. табл. 1). В таблице в столбце AIC показаны оценки критерия Акаика (Akaike information criterion), минимальное значение которого показывает, что модель может быть выбрана как оптимальная. Однако, как показал Шибата Р. [4], для процессов AR критерий Акаика несостоятелен вследствие переоценки порядка модели. В этом случае используют критерий Шварца BIC (Bayesian information criterion), оценки которого состоятельны и в случае процессов AR, в пользу выбора модели говорит его наименьшее значение.

Анализ моделей по таблице 1 показал, что минимальное значение критерия AIC имеет ARIMA(1,1,2), а минимальное значение критерия BIC, при отсутствии автокорреляции в остатках, имеет ARIMA(2,1,0), причем различие BIC с моделью ARIMA(1,1,2) составило всего 0,96 . Средняя ошибка аппроксимации 1,56% модели ARIMA(1,1,2) незначительно, но меньше, чем 1,57% модели ARIMA(2,1,0) . Точечный прогноз средней цены на вторичном рынке жилья в Санкт-Петербурге на 28 апреля 2017 г. по модели ARIMA (1,1,2) составил 1855 долл. США / кв. м, а на декабрь 2017 г. -1858 долл. США / кв. м.

Реальная динамика цен на вторичном рынке Санкт-Петербурга в 2016 г. характеризовалась растущей тенденцией, которая продолжилась в начале 2017 г. (рисунок 2). Оценка этой тенденции в среде R на основе auto.arima показала, что процесс описывается моделью ARIMA(1,1,0) с наличием линейного тренда, автокорреляция в остатках отсутствует согласно критерия Бокса-Льюнга (p-value = 0,94). Прогноз по полученной модели показал значительный рост цен. Так, на 28 апреля 2017 г. прогноз составил 1917 долл. США / кв. м, а на декабрь 2017 г. - 2201 долл. США / кв. м.

t, неделя

Рис. 2. Средняя цена предложения на вторичном рынке жилья г. Санкт-Петербурга с января 2016 г. по февраль 2017 г., долл. США / кв. м [2]

Тенденцию 2016 г. можно аппроксимировать степенной функцией вида: у = 1207,9t ^0,0891 E_t с коэффициентом детерминации R ²=0,87 или линейной функцией с коэффициентом детерминации, равным 0,81. В остатках (e_t) степенной функции наблюдается автокорреляция с коэффициентом 0,5, в то же время дисперсия остатков постоянна по критерию Фишера ( F =1,59 <  F (0,05;27;27) =1,90) и различия средних несущественны по критерию Стьюдента ( t =0,99< t (о,о_5;57) =2,00). Следовательно, остатки степенной функции представляют стационарный процесс, который можно описать моделью ARMA (1,2) , по критерию Бокса-Льюнга ( p-value = 0,85), автокорреляция в остатках отсутствует. Прогноз по полученной модели на 28 апреля 2017 г. составил 1767 долл. США / кв. м, на декабрь 2017 г. - 1832 долл. США / кв. м.

Модели, построенные по еженедельным данным для двух периодов: 02.02.2009-17.02.2017; 15.01.2017-17.02.2017, и прогноз на их основе на май и декабрь 2017 г. представлены в таблице 2. Прогноз, основанный на длительной истории (412 наблюдений) однородных значений средней цены с коэффициентом вариации v=22% имеет незначительную вариацию прогнозной цены. Данные 2016 г. (см. рис. 2) имеют заметную колеблемость, коэффициент вариации v=57% и полученные на их основе прогнозные значения имеют заметную вариацию (см. табл. 2).

Таблица 2

Прогноз на 2017г. средней цены предложения на вторичном рынке жилья г. Санкт-Петербурга, долл. США / кв. м

Модель	AIC	BIC	p-value	Прогноз
				май	декабрь
построена по 412 наблюдениям
ARIMA (1,1,2) : yt = 1,795yt _ 1 — 0,826st _ 1 + 0,113et _ 2 + £t	4396	4412	0,23	1855	1858
ARIMA (2,1,0) : yt = 0,987yt _ 1 + 0,091yt _ 2 + st	4399	4411	0,09	1837	1838
построена по 57 наблюдениям
ARIMA (1,1,0) : yt = 9,1t + 0,6yt _ 1 + st	560	566	0,94	1927	2201
(y t = 1207,9t °,°891 £ t (f t = 1,005 + 0,567^ _i + ^ t — 0,2775 t_i + 0,5655 t_2	251	241	0,85	1769	1832

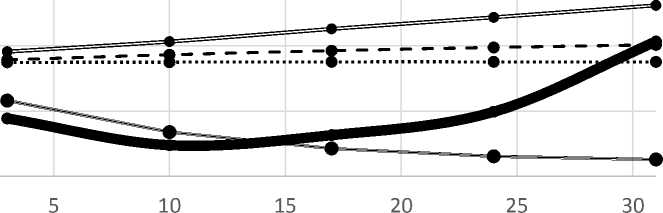
Оценить качество прогноза можно только по факту его свершения. Визуализация значений средней цены вторичного жилья в марте 2017 г. в г. Санкт-Петербурге [2] и прогнозных значений, рассчитанных по моделям, представленным в таблице 2 для этого периода, не позволяет однозначно выбрать лучшую прогнозную модель (см. рис. 3).

CD

ct CD

ARIMмАа(р1т,1,2)

ARIMА (2,1,0)

Фактически

Рис. 3. Средняя цена предложения и прогнозные значения на вторичном рынке жилья г. Санкт-Петербурга в марте 2017 г., долл. США / кв. м [2]

Оценка качества прогноза на март 2017 г., основанная на аналитических показателях, выявила, что минимальные прогнозные ошибки имеет модель на основе степенной функции. Аналитические показатели по рассмотренным моделям представлены в таблице 3, где △ - средняя абсолютная ошибка прогноза; а - среднеквадратическая ошибка прогноза; г - ошибка аппроксимации (средняя относительная ошибка прогноза). У всех моделей, представленных в таблице 3, ошибка аппроксимации не превышает 5%, что свидетельствует o высокой точности прогноза на основе этих моделей. Модель ARIMA (1,1,0) по итогам марта показала наибольшие прогнозные ошибки.

В качестве сравнительного показателя точности прогноза нами был рассчитан коэффициент корреляции (Г уу ) между фактическими (у) и теоретическими значениями (у) (см. табл. 4).

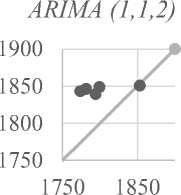
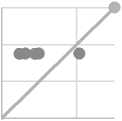
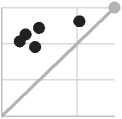
Средняя цена предложения на вторичном рынке жилья г. Санкт-Петербурга в марте месяце имела тесную линейную связь с прогнозными значениями по модели ARIMA (1,1,0) , а с прогнозом на основе степенной функции связь была заметной и носила обратный характер. Таким образом, анализ качества прогноза на основе рассмотренных показателей не выявил однозначно лучшую модель, и для них была построена диаграмма «прогноз-реализация» (см. рис. 4).

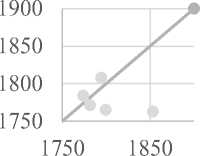
На диаграмме по оси ординат отложено прогнозируемое, а по оси абсцисс – фактическое значение переменной. Прямая линия на диаграмме – это отражение совершенного прогноза. Точечный прогноз по моделям: ARIMА (1,1,2); ARIMА (2,1,0); ARIMA (1,1,0) расположен в зоне переоценки изменений цены. Прогнозные значения на основе степенной функции расположились в двух зонах как переоцен- ки, так и недооценки изменений цены и сосредоточились в окрестностях линии совершенного прогноза. Для этой модели ошибку прогноза разложили на доли несоответствия по Тейлу. Ошибка в оценке центральной тенденции составила 25% (доля смещения). Совпадение стандартных отклонений прогноза и фактических значений – 7% (доля дисперсии). Оставшиеся 68% пришлись на долю ковариации, то есть несистематической, остаточной ошибки, которая при идеальном прогнозе составляет 100%. Таким образом, доля систематической ошибки и вариации составляет третью часть ошибки прогноза, что является хорошим показателем прогнозной модели.

Таблица 3

ARIMA (2,1,0)

ARIMA (1,1,0)

1750 1850

1750 1850

Степенная

Аналитические показатели качества прогноза на март 2017 г. средней цены предложения на вторичном рынке жилья г. Санкт-Петербурга

Модель	д долл.США , кв.м	долл.США σ , кв.м	£, %
построена по 412 наблюдениям
ARIMA (1,1,2) : yt = 1,795yt-1 - 0,826£t-1 + 0,113£t-2 + £t	46,16	51,85	2,58
ARIMA (2,1,0) : yt = 0,987yt-1 + 0,091yt-2 + £t	43,34	46,40	2,42
построена по 57 наблюдениям
ARIMA (1,1,0) : yt = 9,1t + 0,6yt-1 + £t	62,42	65,67	3,48
1 yt = 1207,9t °,°891 £t 1 £t = 1,005 + 0,567£t-1 + 5t - 0,2775t-1 + 0,5655t-2	31,73	44,15	1,74

Таблица 4

Сравнительный показатель качества прогноза средней цены предложения на вторичном рынке жилья г. Санкт-Петербурга, март 2017 г.

Модель	E yy
ARIMA (1,1,2) : yt = 1,795yt-1 - 0,826£t-1 + 0,113£t-2 + £t	0,63
ARIMA (2,1,0) : yt = 0,987yt _1 + 0,091yt _2 +£t	0,43
ARIMA (1,1,0) : 5#t = 9,1t + 0,6yt-1 + £t	0,74
f j/t = 1207,9t °-°891 Et let = 1,005 + 0,567£t-1 + 5t - 0,2775t-1 + 0,5655t-2	-0,43

Рис. 4. Диаграмма «прогноз-реализация» для средней цены предложения на вторичном рынке жилья г. Санкт-Петербурга в марте 2017 г., долл. США / кв. м

Общую оценку качества прогнозной модели дает коэффициент неравенства Тейла ( Theil Inequality Coefficient ), который составил 0,012. Это значение очень близко к нулю, следовательно, прогноз по модели на основе степенной функции хорошего качества. Значение этого коэффициента для трех других моделей тоже близко к нулю, так как не превышает 0,02. Однако, доля систематической ошибки у всех трех моделей ARIMА очень велика и находится в диапазоне от 64% до 91%. Таким образом, прогноз по модели на основе степенной функции можно считать хорошим.

В качестве индикатора прогноза средней цены предложения на вторичном рынке жилья г. Санкт-Петербурга, рассмотрены два показателя: курс доллара США ( USD ) к рублю и цены на нефть марки

Brent, USD /баррель. Коэффициент корреляции между ценой на жилье и курсом USD равен (-0,07), что говорит об отсутствии линейной зависимости, а между ценой на жилье и ценой на нефть – 0,94, то есть тесная линейная связь. Но наличие корреляции между рядами не означает еще совпадения их тенденций. Поэтому временные ряды цены на жилье и цены на нефть были проверены на наличие ко-интеграции с помощью критерия Энгеля-Грангера, который не позволил отклонить гипотезу об отсутствии коинтеграции.

Следовательно, на временном интервале с января 2016 г. по февраль 2017 г. динамика этих показателей не совпадает в течение длительного периода времени. В рамках рассмотренного временного интервала не удалось определить показатель, который можно рассматривать как индикатор средней цены предложения на вторичном рынке жилья г. Санкт-Петербурга. Поэтому строить прогноз будем, опираясь на оптимальную модель, на основе степенной функции. В итоге интервальный прогноз средней цены предложения на вторичном рынке жилья г. Санкт-Петербурга на декабрь 2017 г. составил 1713 – 1954 долл. США / кв. м.