Прогнозирование ценовой динамики акций с помощью модели ARIMA-GARCH
Автор: Архипова А.А.
Журнал: Экономика и бизнес: теория и практика @economyandbusiness
Статья в выпуске: 6-1 (100), 2023 года.
Бесплатный доступ
Цель выполненного исследования - построение модели для прогноза финансовых временных рядов. В статье рассмотрен эконометрический подход, предполагающий построение модели авторегрессии - проинтегрированного скользящего среднего (ARIMA), а также обобщенной модели с авторегрессионной условной гетероскедастичностью (GARCH). В качестве усиления прогнозной силы модели предлагается использование комбинации вышеназванных моделей. Приведено математическое описание этих прогнозных моделей. Построение моделей реализовано в программной среде Python с подключенными библиотеками pandas, numpy, statsmodels, matplotlib. В качестве входных наборов данных импортированы ежедневные значения котировок акций компании Алроса 02.06.2014 по 12.11.2019 г. Результаты исследования показывают, что комбинация моделей ARIMA-GARCH обладает высокой прогнозной точностью и может использоваться для создания краткосрочных прогнозов, а также сделан вывод о переходе к более адаптивным моделям, учитывающим внешние факторы.
Фондовый рынок, прогнозирование, эконометрия, акция
Короткий адрес: https://sciup.org/170198986
IDR: 170198986 | DOI: 10.24412/2411-0450-2023-6-1-14-17
Текст научной статьи Прогнозирование ценовой динамики акций с помощью модели ARIMA-GARCH
На сегодняшний день фондовый рынок представляет собой совокупность экономических отношений, связанных с покупкой и продажей ценных бумаг, оборот которых производится на фондовых биржах. Одна из главных задач инвестора при распоряжении своим капиталом – попытаться найти такие финансовые инструменты, с помощью которых можно увеличить или, как минимум, сохранить свои вложения. В данной статье предлагается изучить и построить модель ARIMA-GARCH для прогнозирования цен акций российского фондового рынка.
Анализ временных рядов
Большое количество исследований, посвященных изучению финансовых временных рядов, показывают, что последние обладают характерными свойствами. Для того, чтобы эконометрическая модель обладала высокой прогнозной точностью, необходимо понимать особенности работы с такими данными. Одной из главных особенностей временных финансовых рядов является наличие волатильности, то есть показателем, который определяет изменчивость цены. Высокая волатильность ха- рактеризуется быстрым, неравномерным изменением цен и большим разбросом, тогда как низкая волатильность означает меньший уровень этих характеристик. Для мира финансов и инвестирования волатильность – очень важное понятие, которым характеризуют финансовые активы. Волатильность является одним из основных способов, позволяющих оценить предполагаемый риск для инвестора [1]. Временные ряды доходности финансовых активов часто демонстрируют кластеризацию волатильности. Кластеризация волатильности – это тенденция больших изменений цен на финансовые активы сгруппироваться вместе, что приводит к сохранению этих величин изменений цен [2].
Отдельно стоит отметить, что в большинстве случаев финансовые временные ряды показывают сильную островершинность (иначе говоря, тяжелые хвосты распределения). Это означает, что распределение таких рядов далеко от нормального. Доказано, что толстые хвосты распределения также являются следствием реакции временного ряда на поступления новой информации. Понимание данных характе- ристик очень важно, поскольку является необходимым при выборе спецификации модели и построении прогнозов. Наиболее распространенными моделями, применяемыми для прогнозирования цен активов, являются модели авторегрессии - проинтегрированного скользящего среднего (ARIMA) [3].
Модель авторегрессии порядка p описывается как (1) и показывает зависимость значения нынешнего периода от прошлых значений периодов p [4]:
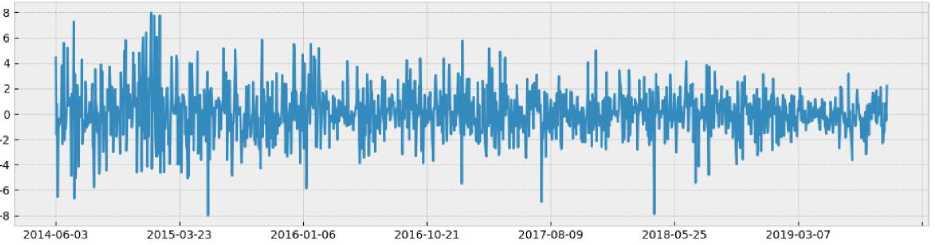
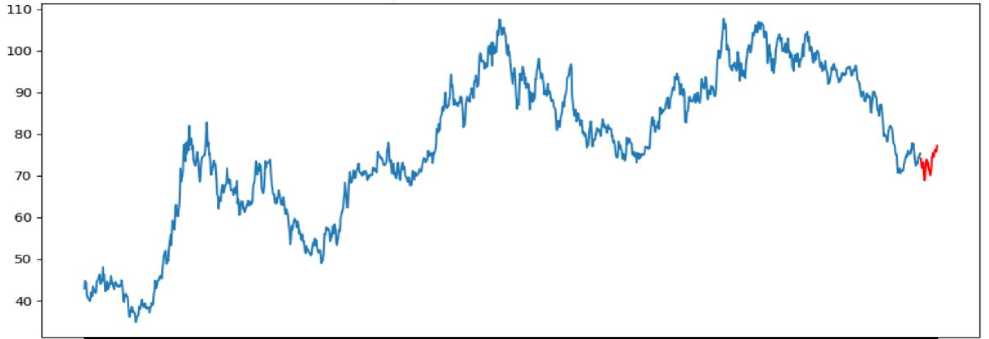
AR(pY yt = с + (piyt—i + - + Модель скользящего среднего порядка q описывается как (2) и показывает зависимость значения нынешнего периода от ошибок предсказания предыдущих q периодов: MA(q): yt = с + Et + 6iEt-i+...+0q£t—q (2) Модель авторегрессии - проинтегрированного скользящего среднего порядков (p, d, q) является суммой моделей AR(p) и MA(q) и может быть представлена в виде (3): У^ = Viyt-1+ - +Ppyt-p+ E -018t_1-...-0qet_q (3) Нестационарный ряд можно привести к стационарному, взяв от исходного временного ряда разность некоторого порядка, т.е. модель ARIMA(p, d, q) предполагает, что разность порядка d временного ряда соответствует модели ARMA(p, q). Множество исследовательских работ было осуществлено в области использования моделей семейства GARCH для прогнозирования волатильности акций, индексов и валют в традиционных финансовых инструментах. В общем виде модель GARCH(P, Q) описывается как (4): yt2 = ш + 51CT2t-1+ ... +6Ра\-Р + Yi£2t-1+ ...+YQ£2t-Q, (4) Модель GARCH прогнозирует будущую дисперсию и ожидает, что ряд является стационарным, за исключением изменения дисперсии, то есть он не имеет трендового или сезонного компонента. На практике модель можно использовать для моделирования ожидаемой дисперсии остатков после применения другой авторегрессионной модели (например, ARIMA). В этом случае GARCH используется для моделирования условной дисперсии, а ARIMA -для моделирования условного математического ожидания. С точки зрения прогнозирования такая модель окажется очень перспективной. Описание набора данных В качестве используемого набора данных используются акции компании АК «Алроса» (ALRS). Рассматриваемый ряд представляет собой ежедневные котировки обыкновенных акций на Российской фондовой бирже в период со 2 июня 2014 года по 12 ноября 2019 года. Данные представлены на графике (рис. 1). Рис. 1. Данные ежедневных котировок АК «Алроса» График анализируемого ряда показывает, что в долгосрочной перспективе уровни ряда сгруппированы на разных средних значениях, а дисперсия ряда явно зависит от времени (разброс значительно варьируется). Это указывает на нестационарность ряда. Чтобы в этом убедиться, был проведен расширенный тест Дики-Фуллера – тест на наличие единичного корня. По результатам теста временной ряд имеет хотя бы один единичный корень (Н0) не отвер- гается). Следовательно, временной ряд не является стационарным. Чтобы избавиться от нестационарности, был взят ряд доходностей (первая разность исходного ряда). Аналогичный тест был проведен для ряда доходностей. Результаты теста показали, что для гипотеза Н0 отвергается. Таким образом, временной ряд доходностей, приведенный на рисунке 2, стационарен. Рис. 2. Ряд доходностей Как было сказано выше, модель ARIMA – это комбинация процессов авторегрессии, интегрирования и скользящего среднего. Для каждой компании были подобраны оптимальные параметры с помощью функции auto_arima из пакета pmdarima. При выборе модели предпочтительной моделью с точки зрения относительного качества выбирается модель с наименьшим значением информационного критерия Акаике. Далее наблюдаемый ряд был проверен на наличие ARCH-эффекта с помощью функции het_arch из пакета statsmodels. В результате проверки выяснилось, что присутствует ARCH-эффект, следовательно, имеет смысл построения модели GARCH на исследуемых остатках. После подбора параметров была получена итоговая модель ARIMA (2, 0, 2) – GARCH (1, 1) и построен прогноз на 30 дней, приведенный на рисунке 3. Рис. 3. Прогнозные значения динамики акций АК «АЛРОСА» (выделены красным цветом) Чтобы увидеть, насколько хорошо мо- пользуется показатель среднеквадратиче- дель соответствует набору данных, ис- ской ошибки (RMSE). Данная метрика по- казывает, насколько далеко в среднем прогнозируемые значения от наблюдаемых значений в модели. В результате расчета RMSE равен 1,57, что говорит о том, что построенная модель обладает высокой предсказательной точностью. Заключение Построенные модели ARIMA-GARCH позволяют сделать вывод о том, что для проведения качественного анализа необходимо большое количество исходных данных. Сильные структурные сдвиги и существенные изменения на рынке оказывают существенное влияние на прогностическую силу модели, поскольку данные изменения учитываются спустя некоторый промежуток времени. Тем не менее, дан- ные модели могут применяться для создания прогнозов в краткосрочной перспективе, поскольку прогнозные значения имеют небольшие отклонения от реальных, особенно в периоды стабильных экономических условий. Существенным недостатком данной модели можно выделить ее ограниченность, поскольку она не позволяет учесть влияние внешних факторов, от которых особенно зависим российский фондовый рынок. Таким образом, для модификации данной модели следует перейти к более адаптивным модификациям. Одной из таких модификаций может выступать ADL-модель, которая позволит включить в анализ дополнительные факторы.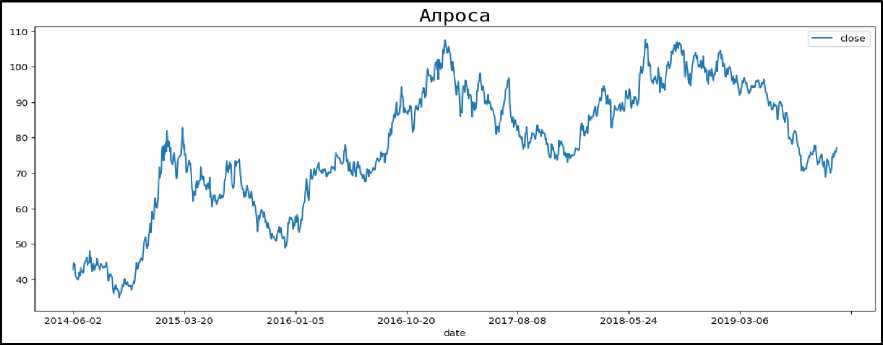
Список литературы Прогнозирование ценовой динамики акций с помощью модели ARIMA-GARCH
- Куссый М.Ю. Методологические аспекты измерения волатильности // Ученые записки Крымского федерального университета имени В.И. Вернадского. Экономика и управление. - 2018. - №1. - С. 59-78.
- Нагапетян А.Р. Кластеризация волатильности доходности акций и динамика диверсификационного потенциала на российском рынке // Теория и практика общественного развития. - 2017. - №6.
- Box G.E.P., Cox D.R. An Analysis of Transformations // Journal of the Royal Statistical Society. Series B (Methodological). - 1964. - №26 (2). - С. 211-252.
- Суслов В.И., Ибрагимов Н.М., Талышева Л.П., Цыплаков А.А. Эконометрия - продвинутый уровень. - Новосибирск: Редакционно-издательский центр НГУ, 2010. - 166 с.


