Прогнозирование цены bitcoin

Рынок криптовалют с каждым годом становится все обширней, появляются новые цифровые активы и постепенно происходит цифровизация экономики. Для того, чтобы понять, что из себя представляет криптовалютный рынок, обратимся к статье [1], в данной статье рассматриваются факторы влияния криптовалют на мировую экономику, показатели капитализации. Авторы данной статьи, выявили следующие показатели капитализации криптовалюты Bitcoin на 20.10.2018:

• -    стоимость (USD): 6 553,11;

• -    капитализация (USD): 113 597 216 367.

Так же в данной статье были выявлены такие факторы влияния, как:

• -    сокращение доли физической наличности в финансовой структуре государства,

• -    изменения в денежных агрегатах,

• -    ограничение или подавление официальных национальных валют.

Рассмотрим факторы, влияющие на волатильность криптовалюты на рынке. Согласно статье [2], факторы подразделяются на 3 группы, а именно: экономические, технические и медийные. В статье [3], ав- тор выдвигает гипотезы о значимости факторов, строит уравнение множественной регрессии и находит корреляционную матрицу, МНК оценки для построенного уравнения регрессии. На основании полученных вычислений, он делает вывод о значимости влияния следующих факторов на курс Bitcoin:

• -    индекс частоты поискового запроса «Bitcoin»,

• -    количество подтвержденных транзакций в сети blockchainбиткоина,

• -    процент капитализации биткоина от общей рыночной капитализации,

• -    ключевая процентная ставка федеральной резервной системы (ФРС) США,

• -    уровень ожидаемой инфляции в США.

Одним из подходов к анализу криптовалютных рынков, являются инструменты стохастического анализа [4]. Авторы предлагают следующий подход к идентификации модели:

• -    построение модели временного ряда;

• -    исследование ряда на стационарность, выделяя в качестве основных средств – расширенный тест Дикии-Фуллера, построение автокорреляционной и частной

автокорреляционной функций. По результатам которого определяется класс используемой модели – ARMA или ARIMA;

• -    подбор параметров модели;

• -    оценка достоверности и адекватности построенной модели, расчет ошибок, критериев AIC, BIC;

• -    разработка прогностических параметров исследуемого временного ряда.

В рамках проведенного исследования модель ARIMA (2,1,2) показала наилучшие результаты, на основе нее был построен прогноз курса Bitcoin, а также получен вывод о том, что уровень перспективности методологии исследования, описанной в данной статье, обладает весьма высокой перспективностью.

Предварительный анализ данных

В выборке представлено 925 значений каждого из временных рядов в течении 3 лет, распределенных по дням, начиная с апреля 2021 г. по март 2024 г, взятых из открытых источников криптовалютных биржевых рынков [5]. Временные ряды и их обозначения представлены ниже:

• -    курс Bitcoin (тыс. $) – price,

• -    курс доллара (руб.) – dol_pr,

• -    общее кол-во BTC в обороте (млн. шт.) – total_btc,

• -    комиссия за транзакцию ($) – fees,

• -    кол-во зарегистрированных уникальных IP-адресов (тыс. адр.) – uniqueaddresses,

• -    цена на момент открытия торгов (тыс. $) – open,

• -    наибольшая цена в течение дня торгов (тыс. $) – high,

• -    наименьшая цена в течение дня торгов (тыс. $) – low,

• -    цена на момент закрытия торгов (тыс. $) – close.

Для начала стоит визуализировать средние значения временных рядов в разрезе лет и посмотреть на общую тенденцию и пропуски во временном ряду, а также выявить выбросы во временных рядах, построив диаграмму типа BoxPlot (рис. 1).

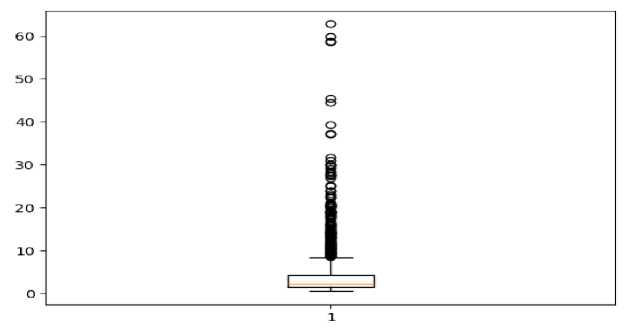
Рис. 1. Определение выбросов в комиссии за транзакцию

В ходе исследования на пропуски во временных рядах, пропущенных значений выявлено не было, при проверке на выбросы, путем построения диаграммы BoxPlot, аномальные значения были выявлены в следующих временных рядах: цена Bitcoin, комиссия за транзакцию, кол-во уникальных IP-адресов, цена Bitcoin на момент от- крытия и закрытия торгов, минимальная и максимальная цена Bitcoin в течение дня торгов, курс доллара. Аномальные значения было принято заменить на медиану (значение, которое разделяет упорядоченный ряд пополам, так что 50% значений находятся выше, а 50% ниже):

Me=x0 +

—

—

' f me-1

f me

i

Далее проверим стационарность рядов с помощью ADF и KPSS тестов. Для оценки статистической значимости результатов данных тестов можно использовать значение p-value. Значения p-value представлены в таблице 1.

Таблица 1. Проверка временных рядов на стационарность

Временной ряд	ADF	KPSS
price	0,70	0,01
total_btc	0,99	0,01
fees	0,56	0,01
uniqueaddresses	0,99	0,01
open	0,70	0,01
high	0,73	0,01
low	0,75	0,01
close	0,71	0,01
dol_pr	0,68	0,01

Исходя из метрик, полученных в таблице 1, можно сделать вывод о том, что все временные ряды не являются стационарными, т.к. значение p-value критерия ADF превышает значение 0,05, а значение p-value критерия KPSS не превышает значение 0,05. Т.к. временные ряды не стационарны, следовательно это может свиде- тельствовать о наличии в них тренда, сезонности или цикличности.

При проверке на наличия тренда, сезонности и цикличности во временных рядах путем построения ACFи PACF функций, во всех временных рядах был обнаружен тренд, в количестве уникальных IP-адресов, рисунок 2, так же была обнаружена сезонная составляющая.

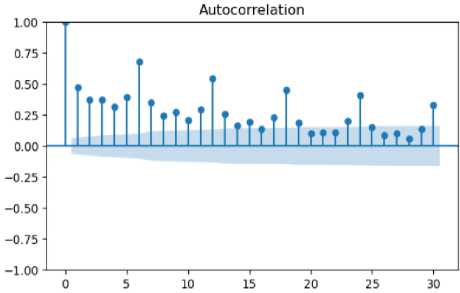
Рис. 2. ACFи PACF уникальных адресов

В следствие того, что временные ряды не стационарны, необходимо изменить данные, применив к ним метод дифференцирования, создания нового набора данных, значениями которого будет являться разница между значениями на текущем и предыдущем лагах (предыдущей даты):

z_t = X t -X t-! .

Первые 5 элементов нового набора данных, полученного путем дифференцирования, представлены в таблице 2.

Таблица 2. Набор данных, полученный путем дифференцирования

date	price	open	high	low	close	dol_pr	fees	uniqueaddresses
04.04.2021	-1,66	-1,5	-1,36	-1,7	-0,62	0,02	-1,57	-0,18
05.04.2021	1,13	1,16	0,98	0,52	0,3	-0,05	3,29	0,14
06.04.2021	0,84	0,41	-0,41	-0,04	-0,87	0,37	1,03	0,08
07.04.2021	-1,03	-0,98	-0,75	-2,05	-2,14	0,53	-2,18	0,02
08.04.2021	-2,07	-2,09	-0,39	0,28	2,27	-0,37	0,89	-0,1

Данные временные ряды являются стационарными. Следовательно мы можем перейти к построению и анализу моделей.

Построение ADL модели

ADL (Модель авторегрессии и распределённого лага) представляет собой эконометрическую модель, используемую для yt = a + Poyt-i + PiXt-i + • где yt представляет собой текущее значение зависимой переменной, α – константа (пересечение), xt-1,..., xt-k - текущие и лагированные значения объясняющей переменной, yt-1,..., yt-k - лагированные значения зависимой переменной, ^0, ^1,..., ^к - коэффициенты регрессии, отражающие влияние объясняющей переменной на зависимую переменную, £t - остатки модели.

анализа связи между зависимой переменной и объясняющими переменными во временных рядах [6]. Она комбинирует ла-гированные значения зависимой переменной и текущие значения объясняющих переменных, ее формула в общем виде выглядит следующим образом:

⁺ P k^xt-k ⁺ P k+1^Xt-k ⁺ ^ t ’

В ходе исследования были построены несколько моделей на 1, 2 и 3 лагах соответственно, наилучшими оказались модели со следующими параметрами: ADL (1, 1, 0, 1, 1, 1), ADL (2, 2, 0, 1, 0, 1) и ADL(3, 3, 1, 0, 0, 3) соответственно, метрики для проверки качества их аппроксимации показали следующие значения, представленные в таблице 3.

Таблица 3. Проверка качества аппроксимации ADL моделей

Показатели качества моделей	ADL (1, 1, 0, 1, 1, 1)	ADL (2, 2, 0, 1, 0, 1)	ADL (3, 3, 1, 0, 0, 3)
RMSE	2,24	2,09	1,99
MAE	1,78	1,67	1,59
MAPE	41,21	39,19	38,51
AIC	-1938,67	-2012,23	-2057,83
BIC	-1929,9	-1974,49	-1999,9

Наилучшей моделью оказалась модель, построенная на 3 лагах, со следующими параметрами, представленными в табли- це 4, так как имеет наименьшие ошибки и критерии Шварца, Акайке.

Таблица 4. Результаты построения ADL модели

Параметр	Коэффициент	p_value
Константа	0,0009	0,71
Apricet-1	-0,7116	~ 0
Apricet — ?	-0,4303	~ 0
Apricet-3	-0,2108	~ 0
Aopen t	0,9992	~ 0
Aopent-1	0,7121	~ 0
Aopen t-2	0,4324	~ 0
Aopent-3	0,2092	~ 0
Ahigh t	0,0053	0,01
Ahigh t-1	-0,0048	0,02

Параметр	Коэффициент	p_value
∆lowt	0,0069	0,01
∆closet	-0,0060	0,01
∆feest	-0,0008	0,47
∆feest-1	0,0046	~ 0
∆feest-2	-0,0014	0,22
∆feest-3	-0,0020	0,07

Остальные параметры были исключены из модели, т.к. не имели влияния на зависимую переменную, что было выявлено путем проведения теста на причинность (способность одного временного ряда влиять на изменение другого), процедура Энгла-Грейнджера. А также были исключены не значимые параметры из таблицы 4, которые имеют значение p_value большее уровня значимости 0,05 (Критерий Стьюдента).

Вычислив необходимые коэффициенты и построив ADL модель, мы можем перейти к прогнозированию изменения курса Bitcoin, относительно предыдущего лага, на протяжении 49 дней и сравнению полученных прогнозных значений с реальными значениями курса Bitcoin.

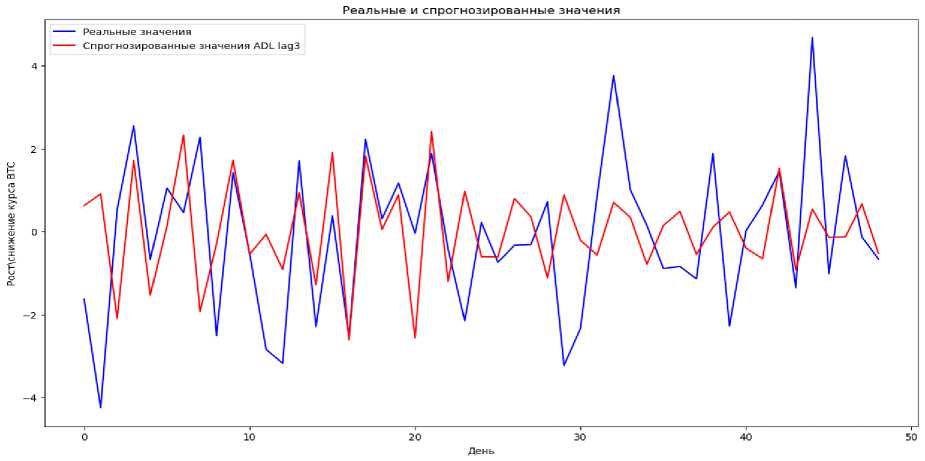
Рис. 3. Спрогнозированные и реальных значения цены Bitcoin

Проанализировав рисунок 3, можно за- составляют 10,72 и 5,08, соответственно, метить следующее, точность предсказания моделью снижения или роста курса Bitcoin. Действительно составляет порядка 61%, как уже говорилось ранее, начиная с 32 по 35 день ADL модель прогнозирует слишком большие изменения цены Bitcoin как в положительную, так и в отрицательную сторону, RMSE и MAE данной модели что является довольно высокими значениями.

Подводя итог, можно сказать, что ADL модели являются недостаточно хорошими для предсказания цены на Bitcoin, данная модель нуждается в дообучении на новых данных и в увеличении лагов, что является весьма ресурсоемким процессом.