Прогнозирование численности Cyclopoida в пойменном озере р. Самара в 2006 г. с помощью моделей авторегрессии
Автор: Дмитриев Виктор Борисович, Герасимов Юрий Леонидович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Водные экосистемы
Статья в выпуске: 3-1 т.15, 2013 года.
Бесплатный доступ
Изучена сезонная динамика численности популяций планктонных веслоногих ракообразных в пойменном озере р. Самара в 2006 году. Были построены стохастические модели для моделирования и прогнозирования численности циклопов, при этом для прогнозирования наилучшей из выбранных оказалась модель AR(1).
Модель авторегрессии, пойменное озеро, циклопы, численность
Короткий адрес: https://sciup.org/148205646
IDR: 148205646
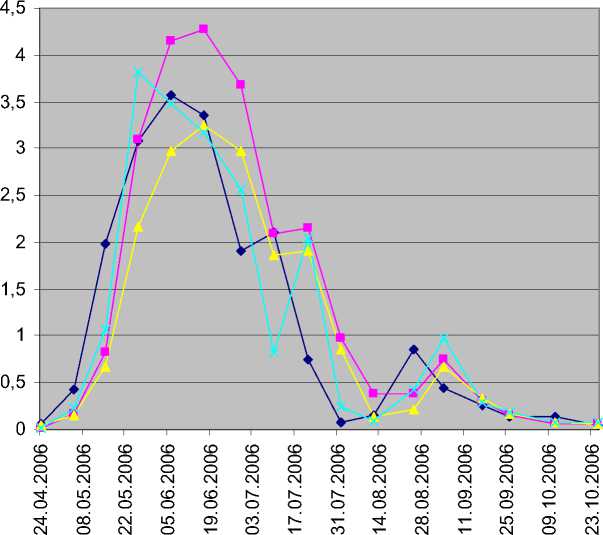
Список литературы Прогнозирование численности Cyclopoida в пойменном озере р. Самара в 2006 г. с помощью моделей авторегрессии
- Гиляров А.М. Динамика численности пресноводных планктонных ракообразных. М.: Наука, 1987. 190 с
- Определитель пресноводных беспозвоночных России и сопредельных территорий. Т. 2. Ракообразные. СПб: ЗИН, 1995. 627 с.
- Балдин К.В., Быстров О.Ф., Соколов М.М. Эконометрика: Учеб. пособие для вузов. 2-е изд., перераб. и доп. М.: ЮНИТИ-ДАНА, 2004. 254 с.
- Основные понятия языка R/Сост. Савельев А.А., Мухарамова С.С., Пилюгин А.Г. Учебно-методическое пособие. Казань, Изд-во Казан. ун-та. 2007. 30 с.
- Использование языка R для статистической обработки данных/Сост. Савельев А.А., Мухарамова С.С., Пилюгин А.Г. Учебно-методическое пособие. Казань, Изд-во Казан. ун-та. 2007. 30 с.
- Lewis W.M. (jun.) Zooplankton community analysts: studies on a tropical system. N.Y.: Springer, 1979. 163 p.
- Кашьяп Р.Л., Рао А.Р. Построение динамических стохастических моделей по экспериментальным данным. Пер. с англ. М.: Наука. Главная редакция физико-математической литературы, 1983. 384 с.
- Миллер, Боткин (Miller R.В., Botkin D.В.). Endangered species: models and predictions. Amer. Sci., 62, 1974. 172-181 pp.
- Герасимов Ю.Л. Зоопланктон водоема в Самарском заречье в 2005 г.//Вест. Самарск. гос. ун-та. 2006, №7 (47). С. 31-36.
- Герасимов Ю.Л. Ракообразные пойменного водоёма реки Самары в черте города Самары//Вестн. Мордовского ун-та, 2010, № 1. С. 118-123.
- Рылов В.М. Cyclopoida пресных вод. Фауна СССР, Ракообразные. Т. 3. Вып. 3. М.-Л.: Изд-во АН СССР. 1948. 318 с.
- Методика изучения биогеоценозов внутренних водоемов. М., 1975. 240 с.
- Руководство по гидробиологическому мониторингу пресноводных экосистем. СПб.: Гидрометеоиздат, 1992. 246 с.
- Gliwicz Z.M., Ghilarov A.M., Pijanowska J. Food and predation as major factors limiting two natural populations of Daphnia. Hydrobiologia, 1981. V. 80, № 3. P. 205-218.
Статья научная
