Прогнозирование чрезвычайных ситуаций с помощью дискретной оптимизации и современных программных средств

Прогнозирование чрезвычайных ситуаций (ЧС) имеет важнейшее значение в деятельности МЧС России. Одними из наиболее сложных для прогнозирования являются синергетические ЧС. В научных исследованиях часто приходится сталкиваться с необходимостью разработки методик оценки риска, рекомендаций по мониторингу и прогнозированию ЧС в отношении некоторой территориальной единицы, определенного объекта или множества объектов. В последнее время при решении такого рода задач довольно часто предполагается выход на некие интегральные показатели риска, вычисленные на основе различных величин и другой имеющейся информации (например, вероятности наступления отдельных событий, карт сейсмической активности, тяжести последствий реализации той или иной опасности, перечня самих опасностей, характерных для деятельности субъекта, результатов анкетирования экспертов и т. д.). Подход на основе единого показателя или небольшого их числа имеет свои преимущества:

единственный интегральный показатель более компактен и в обобщенной форме отражает суть описываемого явления;

части территории или составляющие сложного объекта, в отношении которого производилась оценка риска или прогнозирование ЧС, можно легко ранжировать по значению единственного интегрального показателя.

С другой стороны, этот подход имеет и серьезные недостатки:

в зависимости от применяемой для его вычисления формулы, отдельные параметры риска и ЧС могут усреднять друг друга, скрывая важную информацию;

в общем случае интегрирование отдельных параметров в рамках одного показателя снижает размерность результатов оценки или прогноза, иными словами, мы теряем информацию;

карты с раскрашенными по уровню опасности зонами можно использовать для превентивного размещения сил и средств, но как использовать их в условиях произошедшей аварии и уже развивающейся ЧС?

В рамках работы положим, что синергетическая ЧС — это ЧС, возникшая в ходе (и по причине, и как совокупность) одновременной или последовательной манифестации (проявления) некоторого множества природных и техногенных факторов в течение некоторого относительно небольшого промежутка времени. Ссылка на динамику в данном случае крайне важна: одна произошедшая авария может спровоцировать другую, которая произойдет через некоторое время. Замечание «и по причине, и как совокупность» означает, что каждая следующая авария в цепочке (или, точнее, в дереве — как мы позже увидим, дерево аварий является удобной репрезентацией для данного вида ЧС на концептуальном уровне, хотя оно необязательно столь же удобно с точки зрения реализации моделей в программных средствах), спровоцированная проявившимися прежде факторами, является частью синергетической ЧС, но, помимо этого, сама добавляет факторы для ее дальнейшего развития. Иначе можно сказать, что ситуация в ходе развития синергетической ЧС в каждый конкретный момент определяется (рекурсивно или итеративно — в зависимости от подхода) состоянием объекта в прошлом с момента первой аварии, явившейся триггером для синергетической ЧС. В качестве конца рассматриваемого периода можно взять момент полной ликвидации последствий синергетической ЧС (хотя здесь возможны и другие варианты).

Рассмотрим следующую модель синергетической ЧС. На заданном объекте имеется M единиц оборудования или других потенциальных источников ЧС. Для каждого источника задано N сценариев аварийных ситуаций в некотором фиксированном формате. Такие сценарии могут быть извлечены, например, из декларации промышленной безопасности опасного производственного объекта. В общем случае посредством сценария зафиксированы инициирующие события аварии с параметрами (вероятность / частота события) и параметры, связанные с реализацией опасности по сценарию: вероятность реализации, ущерб, площадь зоны действия поражающих факторов ЧС (или модели, которые следует применять для оценки таковых).

В нашей модели мы рассматриваем три типа синергетических факторов (в общем случае их может быть больше или меньше — принципиально лишь наличие третьего типа факторов из следующего списка): природные (аномально низкая или высокая тем- пература, землетрясение, наводнение, ураганный ветер и т. д.);

внешние техногенные (например, наличие источников вибрации, таких как близлежащая железная дорога или строительная площадка, влияющих на потенциальные источники аварий нашего объекта т. д.);

рекурсивные техногенные (влияние на параметры сценария аварии результатов предварительной реализации других сценариев аварий на рассматриваемом объекте — например, пожар пролива на одном источнике аварии может повлиять на вероятность разгерметизации и / или наличие / отсутствие источника воспламенения, выступающих в качестве инициирующих событий для аварии на другом источнике).

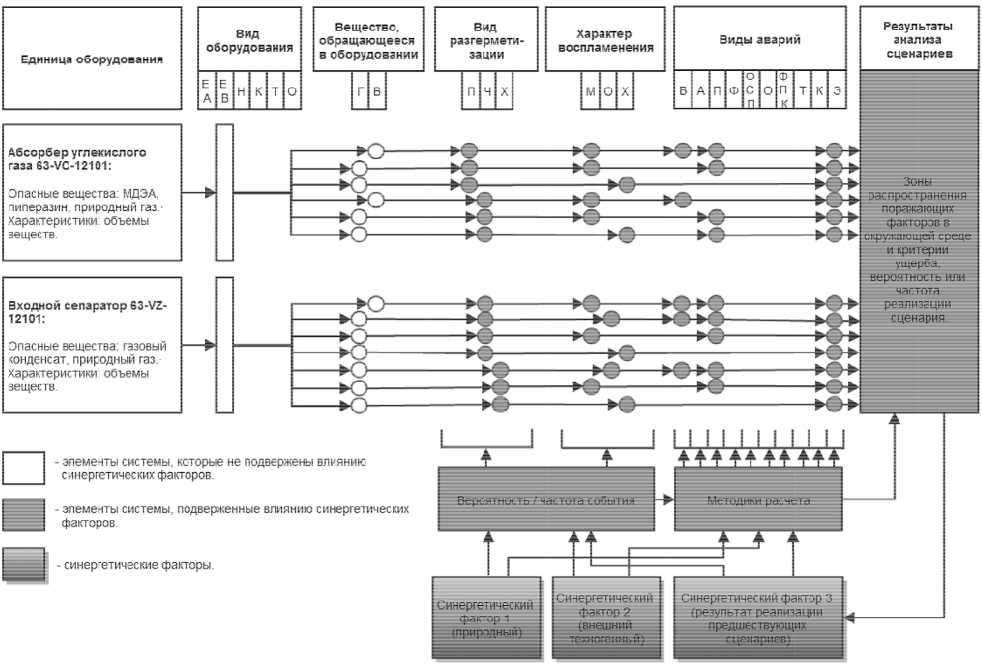
На рис. 1 схематично представлены несколько сценариев аварий (в качестве примера взят конкретный опасный производственный объект) и возможности влияния на их параметры указанных синергетических факторов.

Применительно к рис. 1 приняты следующие обозначения:

вид оборудования или строения: «ЕА» — емкостное оборудование без избыточного давления, «ЕВ» — емкостное оборудование с избыточным давлением, «Н» — насос, «К» — компрессор, «Т» — трубопровод, «ТО» — теплообменное оборудование);

название вещества, обращающегося в оборудовании; «Г» — горючая жидкость, «В» — воспламеняющийся газ);

вид разгерметизации оборудования: «П» — полная, «Ч» — частичная, «Х» — без разгерметизации);

характер воспламенения: «М» — мгновенное, «О» — отложенное, «Х» — без воспламенения;

виды аварии: «В» — взрыв облака ТВС, «А» — физический взрыв, «П» — пожар, «Ф» — факельное горение на аппаратах, «Ф(СП)» — факельное горение по типу «струевое пламя» на трубопроводе, «О» — образование «огненного шара», «Ф(ПК)» — факельное горение по типу «пожар в котловане», «Т» — токсическое поражение, «К» — криогенное поражение, «Э» — экологическое загрязнение.

Как мы видим, в данном случае для каждого сценария рассматривается два инициирующих события (или вида событий): разгерметизация и наличие/от-сутствие источника воспламенения. В общем случае видов инициирующих событий может быть больше или меньше, и они могут иметь иной характер.

В нашей модели мы рассматриваем возможность влияния перечисленных синергетических факторов по двум направлениям:

влияние на частоту / вероятность инициирующих событий;

влияние на параметры реализации сценария аварий, из которых в данном случае нас, в основном, интересуют вероятность / частота реализации и параметры распределения поражающих факторов в пространстве.

Зоны

*<»

>©>

Синергетический фактор 2 = (внешний

Единица оборудования

Веществе, обращающееся в оборудовании

Вид разгерметизации

Характер воспламенения

Виды аварий

Результаты анализа сценариев

- элементы системы, которые не подвержены влиянию синергетических факторов.

элементы системы, подверженные влиянию синергетических факторов.

синергетические факторы.

-Версатнусть 7 чаетета уибы.тия_ ■

Методики-pac чета вид оборудования

Абсорбер углекислого газа 63-VC-12101:

Опасные вещества: МДЭА, пиперазин, природный газ -Характеристики: объемы веществ.

Входной сепаратор 63-VZ-12101:

Опасные вещества: газовый сонденсат, природный газ. Характеристики: объемы веществ.

факторов в окружающей среде ущерба,

♦С-* распространения поражающих

*^—

-ю

—►©•

>^— —*е *©—

♦о-к>

>г»г>

—к> частота реализации сценария.

Синергетический фактор 1

Синергетический фактор 3 (результат реализации

Рис. 1. Общая схема прогноза синергетических ЧС

Для расчета параметров инициирующих событий и параметров реализации сценариев аварий с учетом синергетических факторов применяются либо существующие, либо вновь разработанные модели и методики.

В соответствии с представленной концептуальной моделью, мы имеем:

{ S_z }, z = [1, Z ] — множества параметров внешних природных и техногенных факторов, способных повлиять на параметры сценариев аварий. Считаем, что они одинаково воздействуют на объект в целом и не меняются в ходе расчета, хотя возможны и более сложные варианты.

N пронумерованных сценариев аварий, для каждого их которых:

{ E_{n , in} }, i_n = [1, I_n ], n = [1, N ] — множества исходных известных параметров инициирующих событий I n (определяются по методикам или извлекаются из декларации промышленной безопасности);

{ K_n } — исходные известные параметры вероятности, частоты, ущерба, распределения физических параметров при реализации сценария (извлекается из декларации промышленной безопасности);

( x_n , y_n ) — локальные координаты эпицентра аварии по данному сценарию (например, расположение конкретной единицы оборудования).

На первом этапе расчету подлежат {E'n,in} — параметры инициирующих событий, с учетом воздействия внешних (природных и техногенных) факторов. Это необходимо в том случае, если необходимо просчитать не все возможные цепочки аварий, а только це- почки с наибольшей вероятностью реализации (или с максимальным ущербом) — к вопросу формулирования задачи мы вернемся несколько позже.

Общий принцип работы с моделью таков. В начале расчета выбираем сценарий (например, наиболее вероятный или связанный с наибольшим ущербом). Считаем, что сценарий реализовался, он становится корнем ориентированного дерева (в последствии мы в некотором порядке будем рассматривать в качестве корней и все другие сценарии). Дополнительно формируем динамический контекст, состоящий:

из логического вектора R = [ R n ], n = [ 1, N ] равенство элемента n которого 0 говорит о том, что сценарий еще не рассматривался в качестве реализовавшегося, а 1 — что сценарий уже реализовался;

множества { D } = {({ DP }, DT , DR )}, в каждом элементе которого содержатся числовые параметры { DP }, определяющие зону (в виде множества координат вершин многоугольника-оболочки, центра и радиуса и т. д.) с отклонением от базовых физических параметров (базовые физические параметры рассчитаны с учетом { S_z }), а также сами эти отклонения в виде характера и значения — DT и DR, соответственно (например, «температура» и + A градусов, «источник возгорания» и «Да» и т. д.).

Динамический контекст формируется со значениями по умолчанию для узла-корня, модифицируется, в зависимости от результатов расчетов и передается всем потомкам — в дальнейшем этот процесс повторяется.

В ходе процедуры расчета для текущего n -го узла / сценария (начиная с корня):

• 1.    Пересчитываем { E '' _{n , in} } — параметры инициирующих событий с учетом { S_z } и текущего { D } («текущий» означает либо первоначальный — для корня дерева, либо переданный от родителя — для всех остальных узлов).

• 2.    Рассчитываем { K ' _n } — параметры вероятности, частоты, ущерба, зоны распределения физических параметров с учетом и текущего.

• 3.    Формируем { D '}, дополняя { D } результатами, полученными на шаге 2.

• 4.    Формируем R ', отмечая в R как реализовавшийся текущий сценарий.

• 5.    Формируем узлы-пото м ки из всех сценариев, которые еще не отме че ны в R ' как реализовавшиеся. Передаем им { D '} и R ' в качестве текущих.

• 6.    Организуем обход потомков, для каждого потомка выполняем данный этап, начиная с пункта 1.

• 7.    Возвращаемся к родителю (узлу выше в иерархии). Если родителя нет, то мы в корне дерева и завершаем расчет.

В результате получаем лес деревьев, где каждый путь (ориентированный маршрут) из корня в концевой узел или в узел ветвления — это возможная цепочка аварий (альтернативно можно рассматривать в качестве корня состояние объекта, когда еще ни одна авария не произошла — тогда мы будем иметь дело всего с одним деревом). Поскольку в каждом узле мы храним все параметры соответствующего сценария: параметры инициирующих событий и параметры вероятности всего сценария / ущерба с учетом как природных и внешних техногенных факторов, так и влияния всех аварий, произошедших ранее на маршруте (в цепочке), мы может упорядочивать получившиеся цепочки по объему суммарного ущерба, общей вероятности реализации всей цепочки и т. д. На практике это может означать, что в случае аварии по сценарию № 1 на единице оборудования № 1 нужно не только направлять усилия на ликвидацию аварии на единице оборудования № 1, но также прикладывать силы к предотвращению аварии на некой единице оборудования № 10, которая согласно нашим расчетам имеет наибольшую вероятность случиться следующей (или на единице оборудования № 21, которая имеет наибольшую вероятность произойти после аварии на единицах оборудования № 1 и № 10).

Некоторые замечания относительно представленной модели:

• 1.    Поскольку мы уже учли параметры { S_z } в предварительных расчетах { E ' _{n , in} }, возникает вопрос, зачем дополнительно учитывать эти величины в ходе расчетов { E '' _{n , in} }, на каждом шаге алгоритма? Дело в том, что в ходе построения дерева мы учитываем и эти условия, и текущего { D } вместе. В самом начале мы выполняли расчет только с учетом { S_z } — нам это может понадобиться, если мы выбираем корень дере-

• ва исходя из рейтинга сценариев по вероятности / частоте или ущербу. Однако в общем случае функция расчета параметров инициирующих событий может не быть аддитивной.

• 2.    В данном случае не учитывается, что на одной единице оборудования может реализоваться несколько аварийных сценариев последовательно. То есть сама такая возможность предполагается, но не учитывается, что при реализации сценариев последовательно (например, пролив и через некоторое время пожар разлития) параметры последующего за первым сценария будут иными, чем если бы он и был первым.

• 3.    Анализ выборки деклараций промышленной безопасности объектов показывает, что единый формат описания сценариев аварий отсутствует — его необходимо разработать, как и инструменты для пользователя, позволяющие создать список сценариев в фиксированном формате, пригодном для машинной обработки.

Достоинства представленной модели проистекают из того же источника, что и ее недостатки: модель до тривиальности проста и прямолинейна. С одной стороны, она позволяет получить полную информацию о синергетической ЧС в любой момент времени от ее старта до финиша, но, с другой стороны, этой информации слишком много! В этом нет ничего необычного. Существует несколько широко распространенных эмпирических наблюдений, касающихся анализа данных и моделирования:

• 1.    Больше исходных данных — лучший результат.

• 2.    Простые модели лучше генерализуются (обобщаются, допускают использование для других, в чем-то схожих с исходной, задач).

• 3.    Простые модели лучше сложных (в определенном смысле это следствие из пункта 2).

Проблема в том, что модели, простые концептуально, совершенно необязательно являются таковыми с вычислительной точки зрения. В общем случае, если мы рассматриваем все хоть сколько-нибудь возможные цепочки аварий, суммарное количество узлов во всех наших деревьях (и, следовательно, блоков расчетов, связанных с этими узлами), согласно комбинаторике, составит

N - ¹ N !

L , g = 0 g ^!

что представляет собой число с очень быстрым (сверхэкспоненциальным) ростом при росте числа сценариев N (рис. 2). Таково же количество всех потенциально возможных цепочек аварий, включающих аварии по всем сценариям или только их часть.

Остановимся, чтобы сделать несколько замечаний. В соответствии с предлагаемой концепцией и моделью, синергетическая ЧС существует только в динамике. В самом деле, если мы рассмотрим процесс течения синергетической ЧС, сделав срез на какой-то момент времени, мы увидим одну или несколько аварий, породивших одну или несколько ЧС — без всей информации по объекту (или территории) и изменениям параметров сценариев аварий с момента безаварийного состояния и по данный момент у нас нет ничего, что говорило бы о синергетике. Например, методика прогнозирования ЧС в виде некоторых интегральных показателей, нанесенных на карту, даже если они рассчитаны с учетом баз знаний, содержащих сведения о климатических особенностях и исторические данные о последствиях тех или иных ЧС, может давать актуальные результаты только до момента первой аварии (момента возможного начала синергетической ЧС). Как только первая авария произошла, картина меняется, потому что в силу вступают «Синергетические факторы 3-го типа» (рис. 1) — результаты реализации сценариев предыдущих аварий, и мы вынуждены иметь дело со всей информацией и расчетами, описанными выше.

На данном этапе (хотя на практике стоило бы сделать это раньше) зададимся следующим интересным вопросом: а какую именно задачу мы решаем? «Прогноз» — это предсказание будущего, но что означает «предсказание будущего» в контексте синергетической ЧС? Даже если мы рассчитаем заранее все параметры всех возможных цепочек аварий, что мы будем делать с этой информацией? У нас может быть слишком много вариантов «будущего» для каких-либо конструктивных действий, в частности, мы можем столкнуться с ситуацией наличия множества incomparable optimum (англ. несравнимые оптиму- мы), то есть множества цепочек совершенно различных по составу аварий, но близких по вероятности реализации и/или возможному ущербу. Таким образом, если речь идет о долгосрочном прогнозировании, удобнее именно интегрированные показатели.

На самом деле, рассчитать все параметры всех цепочек попросту невозможно за практически значимое время в силу характеристик такой задачи (рис. 2), а также в силу того, что внешние синергетические факторы могут изменяться, вообще говоря, каждую секунду или чаще.

В такой ситуации приемлемыми и полезными представляются два варианта постановки задачи:

• 1.    В ходе текущего мониторинга, при нахождении объекта или территории в безаварийном состоянии периодически выявлять P наиболее опасных цепочек аварий с точки зрения вероятности, возможного ущерба или их комбинации (то есть риска) с учетом внешних природных и техногенных факторов. Аналогично можно рассчитывать ущерб и вероятность реализации всех цепочек аварий с количеством аварий в цепочке не более K , но в зависимости от величины K это может занять значительное время.

• 2.    Выявить L наиболее опасных аварий, с учетом того, что объект уже находится в процессе развития синергетической ЧС, то есть как минимум одна авария уже произошла. Иными словами, если произошла некая авария, мы должны определить, какие аварии с наибольшей вероятностью могут последовать за ней, принимая во внимание все три типа синергетических факторов.

Вторая задача, по сути, тривиальна (с вычислительной точки зрения), поскольку, используя описан-

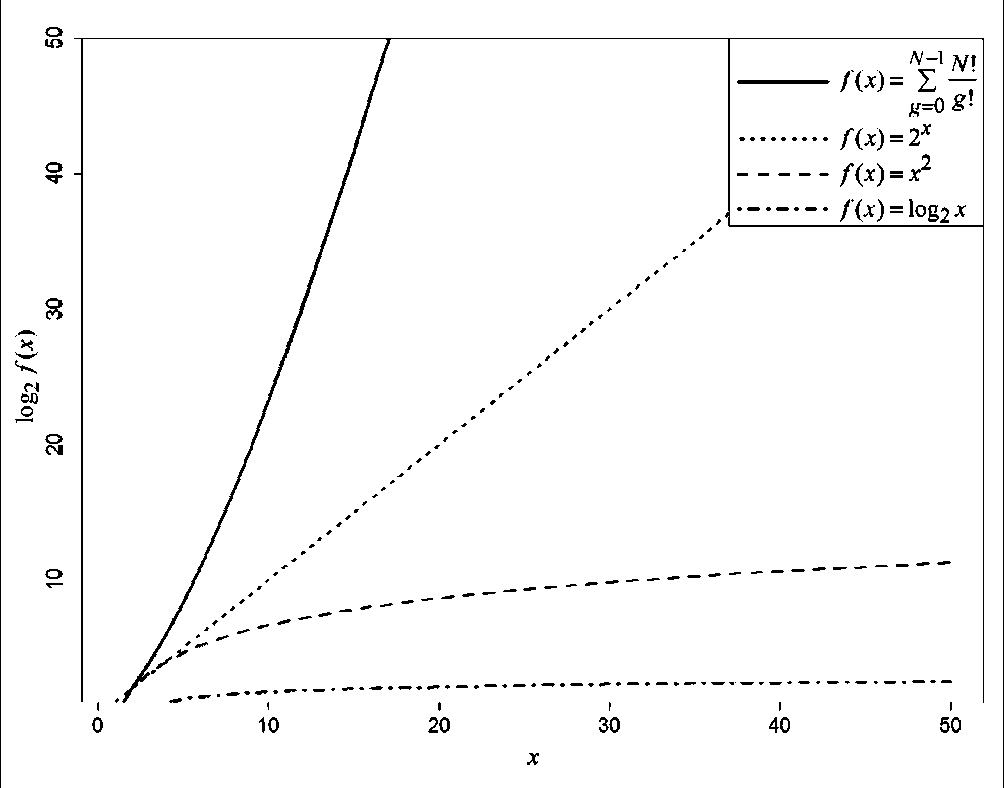
Рис. 2. Сравнение скоростей роста функций (по логарифмической шкале) от x (1)

ные концепцию и модель, мы имеем всю необходимую информацию за прошедшее с начала синергетической ЧС время. Выбрав известный нам узел дерева, то есть узел, символизирующий аварию, которая произошла последней, мы рассматриваем только его потомков и рассчитываем параметры только соответствующих им аварий. Это задача оперативного прогноза, прогноза в динамике, ее решение позволит нам продвигаться параллельно с процессом развития синергетической ЧС, и при этом быть на один или несколько шагов впереди (количество шагов опять-таки зависит от количества

возможных сценариев, и его расчет — это отдельная задача), предпринимая действия по предотвращению последующих аварий.

Первая задача более интересна — в действительности, это NP- задача (2), то есть задача, время решения которой не может быть выражено полиномом некоторой степени, а растет в зависимости от объема исходных данных экспоненциально или сверхэкспоненциально (один из простейших случаев, когда при добавлении одного элемента в вектор исходных данных, количество необходимых для решения задачи операций увеличивается вдвое). Примерами задач того же класса являются задача коммивояжера, задача о рюкзаке, задача Штейнера (3) и другие. Принадлежность задачи к классу NP не означает, что «быстрого» алгоритма ее решения не существует — это говорит лишь о том, что такой алгоритм до настоящего времени не найден.

Такого рода задачи могут решаться посредством методов дискретной оптимизации, в частности, метода ветвей и границ. (4) В данном случае мы можем, например, произвольно выбрать P цепочек аварий в качестве начального решения и обойти все дерево в поисках цепочек, более значимых по своим параметрам, в соответствии с алгоритмом, рассмотренным ранее. Эффективную релаксацию в данном случае выбрать сложно, если вообще возможно, но для сокращения количества рассматриваемых ветвей (а это всегда необходимо, если мы имеем дело с NP- задачами) можно использовать ограничения на:

• вероятность реализации цепочки снизу;

специфику аварий, которые могут происходить на одной единице оборудования или смежных единицах (например, сценарий, предусматривающий пролив с частичной разгерметизацией без воспламенения на единице оборудования 1 не может последовать за взрывом с полной разгерметизацией и воспламенением на той же единице оборудования);

зону распределения физических параметров сценария аварии — рассматриваем только аварии на единицах оборудования, попадающих в таковые зоны родителей (в самом деле, если рекурсивный техногенный фактор не может повлиять на параметры сценария аварии, то такие параметры могут быть оценены отдельно, только с учетом внешних природного и техногенного факторов — нет смысла спускаться по дереву;

• количество аварий, которые могут произойти на одной единице оборудования (в крайнем случае — одна авария на одном источнике);

длину цепочки и т. д.

Если мы дошли до самого низа дерева (или до интересующего нас уровня), то, возможно, следует найти место соответствующей цепочке в списке цепочек решения, в свою очередь удалив оттуда одну цепочку.

Выполнить расчеты согласно рассмотренной модели можно с помощью программы на языке Python 2.7 или 3.3 ( Python имеет развитые средства работы со словарями и списками, что в данном случае весьма удобно) или на другом языке программирования, а также с помощью специализированных программных продуктов Matlab (5), Octave (6) (свободный аналог Matlab ) или R (1) (также свободное программное обеспечение, особенно удобно в сочетании со средой разработки RStudio (7)).

Прогнозирование чрезвычайных ситуаций является весьма актуальной задачей, а прогнозирование синергетических чрезвычайных ситуаций — это еще и задача весьма сложная как с точки зрения построения концептуальных и расчетных моделей, так и с вычислительной. Исследователь, занимающийся данными вопросами, вынужден балансировать между сложностью (в указанных выше смыслах) моделей и расчетов, их точностью и их практической применимостью. Предлагаемые в данной работе подход и модель прогнозирования синергетических чрезвычайных ситуаций, с одной стороны, достаточно сложны, но, с другой, — способны обеспечить большую точность прогноза и демонстрируют возможность применения математических методов и современного программного обеспечения к задачам МЧС России.