Прогнозирование деформационных свойств трикотажа для компрессионных изделий

Компрессионные трикотажные изделия предназначены для обеспечения дозированного давления на участок тела человека. Изделия данной группы являются эффективными функциональными средствами как лечения, так и профилактики ряда заболеваний: варикозного расширения вен, последствий ожогов, послеоперационных и посттравматических отеков.

Давление на тело – основной показатель назначения компрессионных трикотажных изделий, который зависит от нагрузок, возникающих при растяжении трикотажа. Проектирование компрессионных изделий обычно основывается на анализе экспериментальных зависимостей распределенной нагрузки (или напряжения) трикотажа от относительной деформации, получаемых, как правило, при постоянной скорости нарастания деформации (диаграмм растяжения) [1, 2]. Однако во время эксплуатации компрессионного изделия давление на тело не постоянно, а уменьшается в течение носки до некоторого равновесного значения. Несомненный практический интерес вызывает прогнозирование равновесного значения давления компрессионного изделия, а также его взаимосвязь с начальным значением. Вследствие этого проведение комплекса экспериментально-аналитических исследований, направленных на прогнозирование деформационных свойств трикотажа, является актуальной научно-практической задачей.

В качестве объектов при проведении исследований использовались образцы кулирного эластомерного трикотажа для компрессионных изделий лечебнопрофилактического назначения. Технологические параметры исследуемых трикотажных полотен представлены в таблице 1.

Таблица 1 – Технологические параметры исследуемых трикотажных полотен

№ варианта	Базовое переплетение	Вид и линейная плотность сырья	Число петельных столбиков на 10 см	Число петельных рядов на 10 см
1	кулирная гладь	х/б 16,5 текс спандекс 8 текс	170	280
2	ластик 1+1	х/б 16,5 текс спандекс 8 текс	210	264

Для определения взаимосвязи напряжения, деформации и времени нагружения текстильных материалов наиболее часто используют механические модели, которые нашли широкое применение при исследовании деформационных свойств полимерных материалов. Прогнозирование деформационных свойств исследуемых трикотажных полотен предлагается осуществлять на основе обобщенной механической модели Максвелла (рис. 1), характеризуемой двумя средними временами релаксации, которая состоит из трех параллельно соединенных модельных элементов: двух вязкоупругих элементов Максвелла ( E₁₁ - η ₁ и E₁₂ - η ₂ ) и одного упругого элемента E₂ [3, 4].

Рисунок 1 – Обобщенная механическая модель Максвелла, характеризуемая двумя средними временами релаксации

Модель позволяет учитывать составляющие напряжения, обусловленные быстропротекающими и замедленными процессами релаксации, время протекания которых меньше времени одного цикла ношения изделия.

Дифференциальное уравнение механической модели имеет следующий вид:

f l l

П1П2  ,. + ,. + к Ell  E12

E 2 A d² £ (t)

EuE12 J dt2

f        r П П П )) de(t)  „ , .

+ П1 + П2 + E2 "^ +        ,  + E2£(t) = к            к Ell  E12 J J  dt

П1П2 d2o(t) , f П1 ,212 ) do(О , _z. .

--;--+--1----+ CTI t )

E 11 E 12    dt² к E ll   E 12 J   dt

Решение дифференциального уравнения (1) при условии растяжения образца с постоянной скоростью нарастания удлинения c = £ /1 до заданного конечного значения £ = £к и последующей релаксации напряжений имеет следующий вид:

t           t                  (      — £

к

——

а (t) = O oi e T ¹ + a o2 e T ² + E₂ £ _K = c n l — e^{cT 1}

A

e

t

T 1

+ cn

(      — £ к A t

---   —-- l — ecT2  e T2

^{+ E}2 ^£ k ,

к J

к J

где T1 = n1 / E11 и T2 = n2 / E12 - постоянные времени, характеризующие темп быстропротекающих и замедленных процессов

соответственно; o ₀₁ = c n 1

^     -5к cT1

к J

^       -£к 'A

O02 = П 1 — ecT2

к J

релаксации напряжений

– составляющие напряжения,

релаксирующие вследствие быстропротекающих и замедленных процессов соответственно.

Для численной оценки параметров механической модели для исследуемых образцов трикотажных полотен были проведены экспериментальные исследования в режимах растяжения с постоянной скоростью нарастания удлинения и релаксации напряжения. Испытания проводились на автоматизированной разрывной машине «Frank» [5] при следующих условиях: ширина образцов – 50 мм; направление растяжения – вдоль петельных рядов; зажимная длина образцов – 100 мм; скорость деформирования – 100 мм/мин .

По результатам предварительных испытаний для трикотажных полотен получены экспериментальные кривые релаксации напряжения при постоянном удлинении £ _K = 2 и времени наблюдения процесса t_H = 3600 с , произведена оценка параметров уравнения (2), численные значения которых представлены в таблице 2.

Таблица 2 – Результаты математического моделирования процесса релаксации напряжений по выражению (2)

Наименование исследуемых образцов трикотажа	Средние значения параметров выражения (2)					Коэффициент детерминации модели R2	П 1 , МПа·с	П 2 , МПа·с
	т 1 , с	т 2 , с	O oi , МПа	0 02 , МПа	E 2 , МПа
Вариант 1	22	1017	0,738	0,342	0,96	0,951	44,464	184,099
Вариант 2	20	1144	0,098	0,066	0,211	0,952	4,084	40,699

В результате математического моделирования установлено, что практическое использование механической модели с двумя средними временами релаксации позволяет достоверно описать процесс релаксации напряжений исследуемых трикотажных полотен при постоянном заданном значении удлинения. Однако следует отметить, что механическая модель должна быть адекватна результатам эксперимента не только в режиме релаксации напряжения o (t) , но и при других режимах деформирования. При постоянной скорости нарастания удлинения c = £ /1 решение уравнения (1) будет иметь следующий вид:

(

—.

a(s ) = cni 1 — e

^ E l к c ⁿ i

+ С П 2

к

с Ei2 А                  Г       - ⁸

— с

1 — e  ^{c n} 2  + £ 2 8 = c n i 1 — e^cr 1

к        7           к

к      (      8

+ c n 1 — e^c T 2

7     к

к

+ £ 2 8 . (3)

По результатам математического моделирования процесса деформирования трикотажных полотен при постоянной скорости нарастания удлинения с использованием параметров, численные значения которых представлены в таблице 2, установлено, что диаграммы растяжения, полученные путем моделирования, существенно отличаются от экспериментальных. В связи с этим была выдвинута гипотеза о том, что параметры механической модели не являются постоянными, а изменяются в процессе растяжения и зависят от величины удлинения .

Определение зависимостей параметров механической модели от величины удлинения возможно при наличии экспериментальных кривых релаксации напряжения при различных величинах относительной деформации со временем наблюдения t_н , по истечении которого завершаются быстропротекающие и замедленные процессы релаксации напряжений. Однако проведение экспериментальных исследований требует значительных временных затрат, вследствие этого изучалась возможность определения параметров механической модели по результатам более кратковременных испытаний.

Предположим:

– увеличение относительного удлинения приводит к изменению равновесного значения напряжения, равного £28, а также релаксирующих составляющих напряжения а01 и о02, причем данные величины возрастают с увеличением относительного удлинения;

– в процессе растяжения параметры механической модели изменяются таким образом, что средние времена релаксации T₁ и T₂ являются постоянными и не зависят от величины удлинения.

Последнее допущение позволяет определить условное время быстропротекающих t₆ * (3...5)T i и замедленных процессов релаксации напряжения t м * (3„.5)T 2 . Учитывая результаты, представленные в таблице 2, для исследуемых образцов трикотажа принимали t₆ = 100 c . Следовательно, для определения зависимости а ₀₁ ( с ) достаточно провести экспериментальные исследования в режиме релаксации напряжений при времени наблюдения t_H = t₆ при различных величинах относительной деформации 8 к .

Для исследуемых трикотажных полотен проведены испытания в режиме релаксации напряжения при различных значениях деформации 8 к и времени наблюдения t_H = 100 с . По результатам экспериментальных исследований определены зависимости а ₀₁( 8 ) , а затем рассчитаны соответствующие им значения динамической вязкости П 1 ( 8 ) согласно следующему выражению:

(   "- к

П 1 ⁽⁸) = ^ 0i ^{( 8 )/c} • ^{1 —} e^Lc '

к 7

Для математического описания зависимости динамической вязкости n_L (i) ( 8 ) i-го варианта трикотажа (рисунок 2) предлагается использовать следующие соотношения:

ⁿ i(i)^{( 8 )} = K n _L(i) • ⁸ ;                                      ⁽⁵⁾

^п 1(2) ( ^{£ )} = ^К п , (2) ' ^£ ;

где К _{п (i)} - темпы нарастания динамической вязкости n_1(i) , МПа^с.

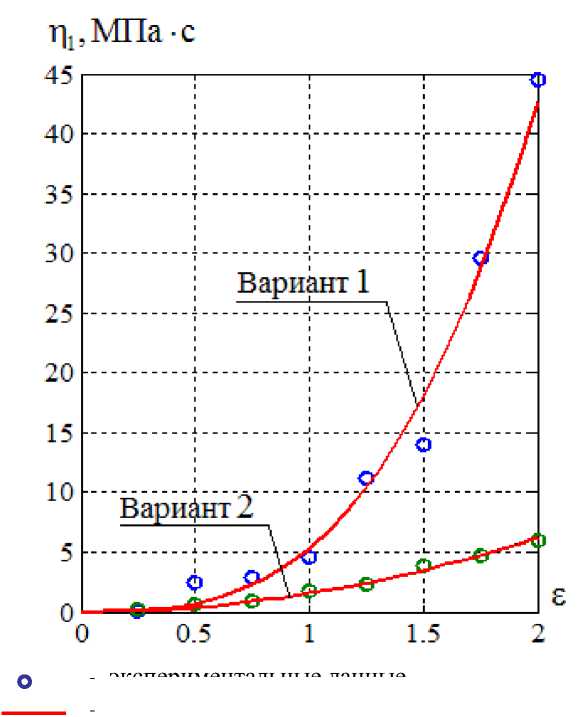
Рисунок 2 - Зависимости динамической вязкости п 1 от деформации £

– экспериментальные данные

– моделирование

Предположив, что общий вид зависимости П 1 ( ^£ ) и П ₂( £ ) идентичен, темпы K _{n (Г)} , К _{п (2} ) нарастания динамической вязкости п ₂ с учетом значений 0 ,2(1) и 0 ,2(2) , полученных в режиме релаксации напряжений при £ _к = 2 (таблица 2), определяется следующим соотношением:

К,2(1) = 002,1,(2)■ К,1(1,. [1 -ec17-]/owlf(7)■ [1 -е Т ];(7)

К,2(2) = 0,2(2)(2)■ К,1(2) ■ [1 -ec7777]/о.1(2)(2)■ [1 -ec7777].(8)

С учетом того, что Т1 и Т2 = const, зависимости Еп(£) и Е12(£) имеют вид: E11(1)(£) = Кп1(1) ■ £ / T1(1) = Ке;;<1) ■ £ ;(9)

Еп(2)(£) = КЧ(2) ■ £2 / T1(2) = Ке„(2) ■ £2;(10)

Е12(1)(£) = Кп2(1) ■ £3 / Т2(1) = Ке,2(1) ■ £;(11)

Е12(2)(£) = Кп2(2) ■ £2 / Т2(2) = Кеп(2) ■ £(12)

где К_{Е (1)} ; К_Е (₂ > ; К_{Е (1)} ; К_{Е (2} ) - темпы нарастания соответствующих модулей упругости, МПа.

Используя выражение (3), на основе массива координат экспериментальных диаграмм растяжения а(е) , найденных параметров Т 1 , Т₂ и зависимостей П i ( е ) , П ₂( е ) сформированы массивы координат равновесной составляющей напряжения [Е₂( е ) • е ; е ] . В результате математического моделирования установлены зависимости E ₂(_l) ( s ) для i-го варианта трикотажа:

^Е2(1)^{( е )} = ^Е20(1) + ^КЕ₂(1) • ^е , ⁽¹³⁾

^Е2(2)^{( е} ) = ^Е20(2) , ⁽¹⁴⁾ где Е ₂₀ (1) и Е ₂₀ ( ₂ ) - начальные значения модуля упругости Е₂ для i-го варианта трикотажа, МПа; К_{Е (1)} — темп нарастания модуля упругости Е₂ трикотажа варианта 1, МПа.

Следует отметить, что для трикотажа варианта 2 модуль упругости механической модели Е₂ постоянен в исследуемом диапазоне деформации. Величины темпов нарастания динамических вязкостей, начальных значений и темпов нарастания модулей упругости для исследуемых трикотажных полотен представлены в таблице 3.

Таблица 3 – Величины темпов нарастания динамических вязкостей, начальных значений и темпов нарастания модулей упругости

Наименование исследуемых образцов	Кп , МПа • c П 1	КП2, МПа • c	KF , МПа Е 111	КР , МПа Е 12 1	Е20, МПа	KF , МПа Е2 7
Вариант 1	5,337	22,097	0,243	0,022	0,161	0,1
Вариант 2	1,55	10,474	0,078	0,009	0,21	-

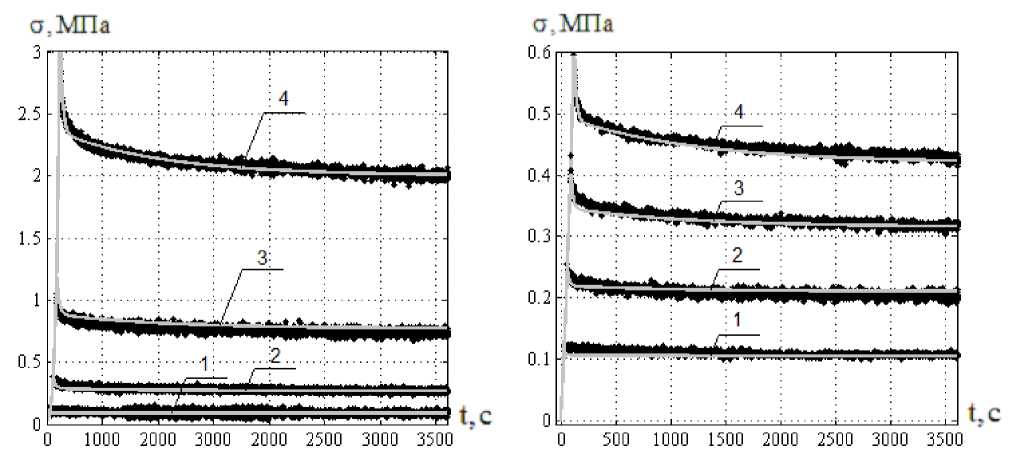
Вариант 1                               Вариант 2

– экспериментальные данные;       – результаты моделирования

Рисунок 3 – Кривые релаксации напряжений трикотажных полотен:

1 - е = 0,5 ; 2 - е = 1 ; 3 - е = 1,5 ; 4 - е = 2