Прогнозирование доходной части муниципального бюджета посредством нечеткой логики

оказывающих существенное влияние на соответствующие следствия. Малозначимые причины считаются «бесконечно малыми» и не рассматриваются. В этом состоит удобство и простота модели (не в ущерб ее адекватности). Существенность влияния экономических параметров определяется экспертным путем и с помощью математических методов. Допускается также перекрестное влияние причин, более того, за исходными величинами кроются и другие экономические показатели.

Исходя из обозначенных принципов, рассмотрим методику прогнозирования макроэкономических процессов посредством нечеткой логики:

• 1.    Постановка задачи. Выделение существенных причин, влияющих на следствие. Составление принципиальной схемы модели (иерархии). Экономическое и математическое обоснование схемы. Сбор числовых данных.

• 2.    Математические действия с числовы-

• -    формализация; -    обработка; -    интерпретация.

• 3.    Ретропрогноз. Оптимизация и корректировка модели.

• 4.    Собственно прогнозирование, корректное задание входных показателей.

В качестве примера рассмотрим экспериментальную модель для прогнозирования поступления налога на прибыль в муниципальный бюджет (рис. I).

ми данными:

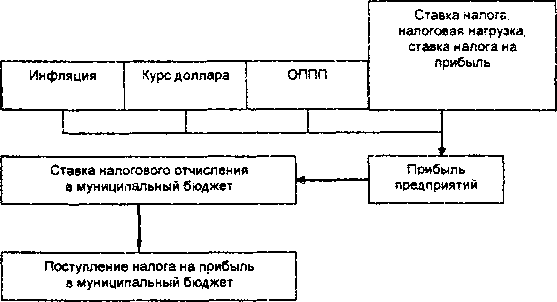
Рис. 1. Принципиальная схема нечеткой математической модели для прогнозирования поступления налога на прибыль в муниципальный бюджет.

Для прогнозирования прибыли предприятий в данной схеме используется четыре основных входных показателя: Инфляция, Курс доллара, Объем производства промышленной продукции (ОППП), Налоговая ставка. Данные показатели условно можно разделить на три группы:

• 1.    Показатели, связанные с макроэкономической ситуацией в стране. В данном случае - это Инфляция и Курс доллара. Несмотря на «похожесть» этих экономических явлений, абсолютные значения их прироста, как увидим ниже, существенно различаются. Следовательно, целесообразен учет и того и другого показателя. Влияние данных показателей очевидно, так как они меняют реальную стоимость денег.

• 2.    Показатели, связанные непосредственно с деятельностью самих предприятий. В данной модели учтен всего один, на наш взгляд, существенный показатель - Объем производства промышленной продукции (ОППП).

• 3.    Показатели, связанные с налоговыми ставками, - «административная» составляющая. В данной модели учитывается Ставка налога на прибыль. Вообще говоря, на деятельность предприятий большее влияние оказывает Налоговая нагрузка (суммарное налогообложение). Уровень налогообложения предприятий оказывает прямое и очень весомое влияние на их функционирование.

И наконец, полученный прогноз прибыли предприятий позволит непосредственно вычислить налоговые поступления в городской бюджет. С этой целью в схему включена Ставка налогового отчисления в муниципальный бюджет.

Взаимовлияние показателей. Возможности задания входных параметров. Сценарные посылки. Временной интервал прогнозирования.

Нетрудно заметить, что рассмотренные выше четыре входных показателя оказывают взаимное влияние друг на друга. Например, Инфляция и Курс доллара во многом являют- ся «схожими» по своей экономической природе. Более того, от них зависит и деятельность предприятий - объем промышленной продукции в частности.

Интересно отметить, что в рассмотренной схеме неявно учитываются и другие экономические показатели. Например, за Инфляцией кроется уровень экономической стабильности, рост цен на продукцию естественных монополий (а значит, и увеличение издержек предприятий), предпосылки экономического роста и т. д. Увеличение объема промышленной продукции может быть связано с открытием новых предприятий, благоприятным инвестиционным климатом.

Нечеткая математическая модель позволяет учесть данные особенности.

Другим важным вопросом выступает адекватное задание значений входных показателей и «очевидность» их задания. В этом смысле «очевидными» являются Инфляция и Курс доллара. Иными словами, в рамках реалистического сценария (стабильной ситуации в стране в ближайшем будущем) соответствующие входные значения данных двух параметров «очевидны», тем более что они задаются не точечно (одним значением), а интервально.

Целесообразно рассмотреть также второй - критический сценарий, связанный, например, с девальвацией рубля.

Легко задать и налоговую ставку. Это обусловлено тем, что об увеличении или уменьшении налогов известно, как правило, заранее. Данное обстоятельство сразу же позволит изменить входной показатель и получить соответствующий прогноз. Причем может сложиться такая ситуация: планы, скажем, об увеличении ставки налога так и останутся планами, в то время как руководители предприятий уже выведут часть возможной прибыли в другие статьи бухгалтерской отчетности.

Наиболее затруднительно задание изменения объема производства промышленной продукции. Здесь используется метод экстраполяции трендов (изучение возможных вариантов развития), метод экспертной оценки. В перспективе предполагается более детальная проработка данного блока математической модели, и даже создание некоторой

«надстройки» в иерархии для прогнозирования данного показателя.

Особенность данной модели - тесная взаимосвязь прогнозирования и процессов принятия управленческих решений. То есть существует возможность получить гипотетический прогноз изменения поступления в бюджет налога на прибыль в случае принятия некоторых управленческих решений (изменение налоговых ставок, контроль макроэкономической стабильности на федеральном уровне; изменение экономической политики предприятий управленческим персоналом на местном уровне).

Обратная задача - рассматривая гипотетически желательную наполняемость бюджета по данному налогу, получить некоторый набор возможных исходных параметров (то есть «что нужно сделать для достижения желательного уровня наполняемости бюджета по данной доходной статье»). Обратная задача имеет многозначное решение.

Таким образом, большое внимание в процессе прогнозирования необходимо уделять некоторым событиям.

Временным интервалом прогнозирования выступает календарный год.

Исходные данные. Математическая формализация данных с помощью нечетких множеств. Ретроанализ. Базовая матрица.

Рассмотрим участок блок-схемы «Курс доллара + Инфляция + Объем промышленного производства -» Прибыль предприятий».

Исходные данные, на которых базируется нечеткая математическая модель, представлены в табл.1.

В данной нечеткой математической модели рассматриваются в основном только темпы изменения показателей. Темп курса доллара данного года характеризует прирост курса доллара в данном году по отношению к предыдущему году. Инфляция данного года представлена в разах по отношению к предыдущему году. Темп объема производства промышленной продукции - в сопоставимых ценах: в разах к предыдущему году с учетом инфляции данного года. И наконец, темп прибыли предприятий представлен в разах к предыдущему году в фактических (номиналь-

Таблица 1

Исходные данные

Год	Курс доллара (рублей за 1$)	Темп прироста курса доллара (в разах, к предыдущему году)	Инфляция (в разах, к предыдущему году)	ОППП (тыс. руб.)	Темп прироста ОППП (сопоставимые цены, в разах, к предыдущему году)	Прибыль предприятий (тыс. руб.)	Темп прироста прибыли (номинальные цены, в разах, к предыдущему году)
1995	4,64		2,5	1459		309879,0
1996	5,56	1,198275862	1,212	1793,688	1,0143527	143849	0,4642102
1997	5,96	1,071942446	1,098	2026,214	1,02881211	194311	1,3507984
1998	20,65	3,464765101	1,635	4174,74	1,26016196	692455	3,5636428
1999	27	1,307506053	1,369	5917,90	1,03546337	1379742	1,9925367
2000	28,14	1,042222222	1,197	9828,02	1,38740821	2007796	1,4551967
2001	30,14	1,071073205	1,182	12570,23	1,0820806	1428787	0,7116196

ных) ценах. При этом предполагается, что Инфляция, Темп прироста курса доллара и Темп прироста ОППП в данном году вызывают Темп прироста номинальной прибыли предприятий в данном году.

На практике очень часто бывает затруднительным определить вклад каждой причины в следствие. В рассматриваемой модели эта проблема решается следующим образом: для каждого года представим следствие (прирост номинальной прибыли) в виде суммы нечетких вкладов трех причин. Возьмем для примера 1997 год.

Сначала находим сумму темпов причин (табл. 2).

Таблица 2

Сумма темпов причин

Год	Темп прироста курса доллара (в разах, к 1996 г.)	Инфляция (в разах, к 1996 г.)	Темп прироста ОППП (сопоставимые цены, в разах, к 1996 г.)	Сумма темпов причин (в разах)	Темп прироста прибыли (номинальные цены, в разах к 1996 г.)
1997	1,0719424	1,098	1,02881211	3,198754559	1,3507984

Составим нечеткое множество D(1997) доли темпа прироста курса доллара в суммарном темпе (рис. 2):

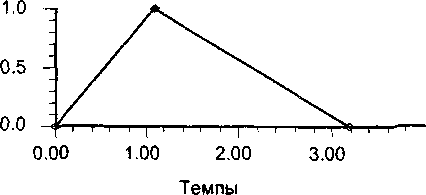
Рис. 2. Доля темпа прироста курса доллара в суммарном темпе.

были признается вклад в

1,0719424 / 3,198754559 = 0,335712%.

Вычислим пропорциональную долю прироста темпа номинальной прибыли предприятий. Для этого умножим вклад доллара в процентах на темп прироста номинальной прибыли:

0,335112 х 1,3507984 = 0,452669.

Составим соответствующее нечеткое множество R(D1997) части темпа прироста курса доллара в приросте номинальной прибыли (рис. 3):

Данное нечеткое множество представляет собой треугольник с вершинами: (0; 0), (1,0719424; 1), (3,198754559; 0). (Сторону треугольника, лежащую на оси абсцисс, далее будем называть основанием треугольника, две другие стороны, то есть функцию принадлежности, будем также называть боковыми сторонами.} Истинным вкладом темпа курса доллара в изменение номинальной при-

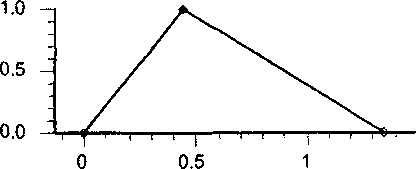
Темп прироста номинальной прибыли

Рис. 3. Доля темпа прироста курса доллара в темпе прироста номинальной прибыли.

Данное нечеткое множество имеет вершины (0; 0), (0,452669; 1), (1,3507984; 0).

Таким образом, между рассмотренными двумя множествами (основаниями треугольников), а значит - и функциями принадлежности (соответствующими боковыми сторонами треугольников) установлено взаимнооднозначное соответствие (строгое доказательство данного факта опустим). Вычислим коэффициент прямого отображения:

D(1997)-*R(D1997).

Для этого разделим темп прибыли на сумму темпов трех причин:

К(1997) = 1,3507984 / 3,198754559 = 0,422289.

Поясним экономический смысл выше-проведенных операций (рис. 4).

Функция принадлежности прироста курса доллара

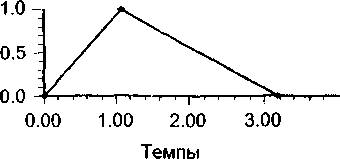
Рис. 4. Отображение темпа прироста курса доллара в долю темпа прироста номинальной прибыли.

Доля темпа прироста курса доллара в темпе прироста номинальной прибыли

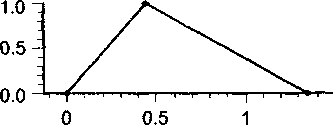
Темп прироста номинальной прибыли

Как было отмечено выше, темп курса доллара 1,0719424 обуславливает 0,452669 темпа прироста прибыли (геометрически это соответствует отображению самых верхних точек треугольников - рис. 4). Данный факт признается истиной. Однако на практике это далеко не всегда так. На самом деле изменение темпа курса доллара может вносить больший или меньший вклад в темп номинальной прибыли. Графически это означает сдвиг по функции принадлежности (боковым сторонам левого треугольника на рис. 4) вправо и влево соответственно. То есть доллар «занимает» или перекрывает у других причин больший или меньший процент влияния на следствие. По мере удаления от истинного значения возможность, скажем, большего влияния темпа доллара на следствие (вклад темпа доллара в темп прибыли) падает. Иными словами, сдвигаясь по правой стороне левого треугольника (на рис. 4) вниз, соответствующие значения функции принадлежности убывают до нуля. И невозможным признается факт 100%-го влияния темпа курса доллара и только его на 100%-ый прирост номинальной прибыли (правые нижние точки треугольников на рис. 4). Аналогичные рассуждения можно провести и для уменьшения процента темпа доллара в сумме темпов. Ложным признается абсолютное невлияние темпа курса доллара на изменение прибыли (левые нижние точки треугольников на рис. 4).

Следует заметить, что данная схема имеет и другой смысл. Так как между функциями принадлежности установлено взаимнооднозначное соответствие, то речь, вообще говоря, идет о линейной функциональной зависимости доли темпа прироста номинальной прибыли от фактического значения прироста курса доллара, причем коэффициенты линейного отображения между левыми и правыми сторонами треугольников будут различными. Именно данное обстоятельство и будет использоваться в прогнозировании. Возникает вопрос: почему рассматривается именно линейная зависимость, а не какая-либо другая?

Во-первых, на достаточно малом расстоянии от точки истинности более удачным является именно линейное приближение.

Во-вторых, в прогнозировании используется вычисление центра тяжести нечетких множеств, и, даже если графическое изображение данных зависимостей имеет вид кривых вблизи точки истинности, это не вызовет сколь-нибудь существенный сдвиг результата (центра тяжести нечеткого множества) вправо или влево.

Разумеется, по мере удаления от точки истинности вправо или влево возможность данной линейной зависимости убывает до нуля.

Таким образом, нами рассмотрен нечеткий вклад прироста курса доллара в прирост номинальной прибыли.

Точно такой же алгоритм используется для построения двух других отображений:

• 1 . I (1997) -> R(I1997) - нечеткий вклад инфляции в долю прироста номинальной прибыли.

• 2 .0(1997) -> R(01997) - нечеткий вклад изменения реального объема производства промышленной продукции в долю прироста номинальной прибыли.

Соответствующие графические изображения представлены на рис. 5 и 6:

Функция принадлежности                             Доля темпа прироста курса доллара прироста инфляции                              в темпе прироста номинальной прибыли

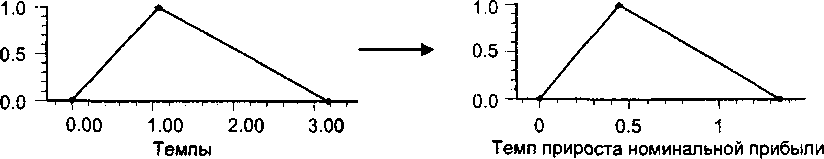
Рис. 5. Отображение темпа прироста инфляции в долю темпа прироста номинальной прибыли.

Функция принадлежности прироста ОППП

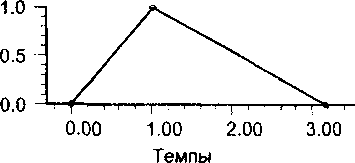
Рис. 6. Отображение темпа прироста ОППП в долю темпа прироста номинальной прибыли.

Доля темпа прироста ОППП в темпе прироста номинальной прибыли

Ретроанализ: Сложим нечеткие множества следствий (при сложении нечетких множеств складываются абсолютные значения соответствующих трех точек функции принадлежности):

Ss= R(D1997) + R(l 1997) + R(O1997).

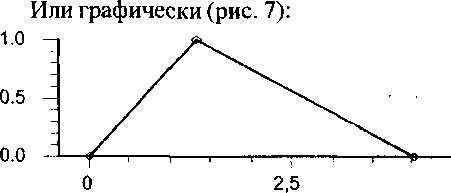
Темп прироста номинальной прибыли

Рис. 7. Сумма нечетких вкладов причин.

В результате получен в точности истинный темп прироста номинальной прибыли в 1997 г. - точка (1,3507984; 1).

Итак, ретроанализ показал истинную ситуацию 1997 г.

Базовая матрица нечеткой математической модели.

Проведем вышеперечисленные операции по данным каждого года. В результате получим базовую матрицу нечеткой математической модели, с помощью которой и будет осуществляться прогнозирование (табл. 3).

В каждой ячейке данной матрицы содержится нечеткое число, с функцией принадлежности -треугольником. В каждой строке

мн

Таблица 3

Базовая матрица нечеткой математической модели

Год Нечеткие вклады соответствующих причин по годам Нечеткие результаты соответствующих нечетких вкладов по годам 1996 D(1996) 1(1996) 0(1996) R(D1996) R(I1996) R(O1996) 1997 0(1997) 1(1997) 0(1997) R(D1997) R(I1997) R(O1997) 1998 0(1998) 1(1998) 0(1998) R(D1998) R(I1998) R(O1998) 1999 0(1999) 1(1999) 0(1999) R(D1999) R(I1999) R(O1999) 2000 0(2000) 1(2000) 0(2000) R(D2000) R(12000) R(02000) 2001 0(2001) 1(2001) 0(2001) R(D2001) R(I2OO1) R(O2001) имеются три пары нечетких множеств соответствующих причин и следствий, между которыми установлены взаимно-однозначные соответствия. Коэффициенты линейного отображения оснований функций принадлежности соответствующих нечетких множеств (оснований соответствующих треугольников) - К(1996), ... , К(2001) [в матрице не представлены] являются, очевидно, одинаковыми для каждого из трех отображений в данной строке.

Суммы нечетких причин и суммы соответствующих следствий по данной строке показывают истинную ситуацию данного года.

Экспериментальный прогноз поступления налога на прибыль в муниципальный бюджет в 2002 году.

В качестве входных значений параметров выбраны следующие интервалы (фактичес- кая данность за 2002 год):

Курс доллара (30,69; 31,68), Темпы прироста (1, 03226; 1, 04268);

Инфляция (1,12; 1,16);

ОППП(1,05; 1,1).

С помощью данных интервалов получены приближения ситуации 2002 года к ситуации каждого из предыдущих лет.

То есть получена аппроксимирующая матрица нечеткой математической модели. Функции принадлежности каждого элемента данной матрицы представляют собой трапецию. Существует несколько способов обработки и интерпретации аппроксимирующей матрицы. Прогнозы, полученные наиболее эффективными, на наш взгляд, методами, представлены ниже. Не вдаваясь в математическую и экономическую сущность данных процессов, рассмотрим полученные результаты (табл. 4):

Таблица 4

Прогнозы номинальной прибыли предприятий в 2002 г.

Тип прогноза	Коэффициент прироста номинальной прибыли по отношению к 2001 г. (в разах)	Соответствующие значения ожидаемой номинальной прибыли предприятий в 2002 г. (тыс. рублей)
Метод максимальных значений прогностической матрицы (интервальная оценка)	1,40363-1,47135	2005490-2102250
Метод максимальных значений прогностической матрицы (точечная оценка)	1,43754	2053940
Метод интеграции прогностической матрицы (Коэффициент значимости = 0, 95)	1,33128	1902120
Метод интеграции прогностической матрицы (0, 95) с высокой площадью возможности (интервальная оценка)	1,27286- 1,48482	1818650-2121490
Метод интеграции прогностической матрицы (0,95) с высокой площадью возможности (точечная оценка)	1,37902	1970330
Прогноз финансового управления городской администрации	1, 3865	1981000

Апостеори можно утверждать, что полученные темпы прироста номинальной прибыли предприятий в 2002 г. вполне могут бьггь согласованы с уменьшением процентной став ки налога на прибыль предприятий с 39 до 26% в 2002 году. (Данные об отклике изменения номинальной прибыли предприятий на уменьшение налоговой ставки отсутствуют.)

Далее из данных значений номинальной прибыли необходимо вычесть ожидаемый налог на имущество предприятий и результаты умножить на процентную ставку отчисления налога на прибыль в муниципальный бюджет, которая представляет собой также нечеткое число (эмпирическое поступление налога в предыдущие годы при данной ставке составляет 10-14%; рис. 8):

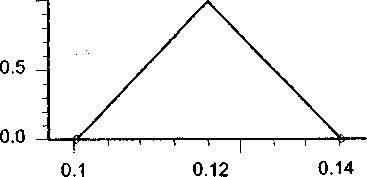
Рис. 8. Норматив отчисления налога на прибыль в муниципальный бюджет.

В итоге:

Таблица 5

Прогнозы ожидаемого поступления налога на прибыль в муниципальный бюджет

Тип прогноза	Общий интервал поступления налога на прибыль в местный бюджет (тыс. руб.)	На уровне значимости Alpha = 0, 95 (тыс. руб.)	Точечная оценка методом центроида (тыс. руб.)
Метод максимальных значений прогностической матрицы (интервальная оценка)	183049-273875	220608 - 233853	227916
Метод максимальных значений прогностической матрицы (точечная оценка)	187894-267112	225247 - 229208	227383
Метод интеграции прогностической матрицы (Коэффициент значимости = 0, 95)	172712-245856	207180-210837	209164
Метод интеграции прогностической матрицы (0, 95) с высокой площадью возможности (интервальная оценка)	139058-276638	196701 - 236945	212052
Метод интеграции прогностической матрицы (0, 95) с высокой площадью возможности (точечная оценка)	179532-255405	215296-219090	217348
Прогноз финансового управления городской администрации	178120
Факт за январь - октябрь 2002 года (10 месяцев)	204814,1

Следует отметить, что представленные способы формализации, обработки и интерпретации числовых значений экономических показателей не являются единственными. Имеются широкие возможности для усиления модели как с экономической, так и с математической точки зрения.