Прогнозирование финансовых временных рядов с использованием рекуррентных нейронных сетей LSTM

НЕЙРОННЫХ СЕТЕЙ LSTM

Таблица 1 – Исходные данные инструмента

						Close
2016-02-01	10:05	9797	9797	9710	19876	9735
2016-02-01	10:10	9735	9736	9704	8611	9730
--------	--------	--------	--------	--------	--------	--------
2018-02-01	23:45	26490	26490	26480	183	26481
2018-02-01	23:50	26480	26485	26472	649	26484

Для улучшения работы нейронных сетей воспользуемся нормализацией данных в пределах [0 : 1] [9] (см. табл. 2).

Таблица 2 – Нормализация данных инструмента

						Close
2016-02-01	0.0000	0.0246	0.0233	0.0201	0.1927	0.0211
2016-02-01	0.0037	0.0211	0.0197	0.0197	0.0835	0.0281
2016-02-01	0.0074	0.0208	0.0195	0.0184	0.0978	0.0195
2016-02-01	0.0111	0.0195	0.0183	0.0173	0.1271	0.0176
2016-02-01	0.0148	0.0178	0.0181	0.1794	0.0862	0.0189

Рекуррентные нейронные сети будут принимать в качестве входных данных последовательность значений, в данном случае в качестве входных данных будет использована матрица, состоящая из 6 признаков и фиксированного скользящего окна длиной n (см. рис. 1).

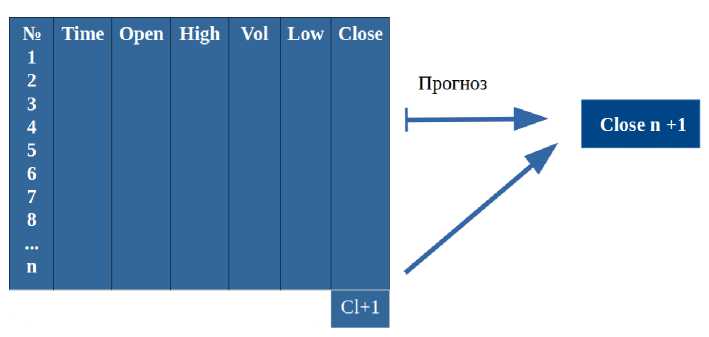
Рисунок 1 – Данные для обучения модели рекуррентных слоев

Используем в качестве переменной скользящего окна значение n = 20, а также разделим выборку в соотношении 90 : 10 на тренировочные данные и данные для проверки гипотезы (отложенные данные). Также выделим 10 % от тренировочных данных на тестирование алгоритма.

Таким образом получим следующее соотношение: – данные для тренировки: 75713 × 20 × 6;

– данные для тестирования: 8413 × 20 × 6.

Конструирование нейронной сети показано на рис. 2.

Тип слоя         Входной Рекуррентный Рекуррентный Агрегирующий Выходной слой          слой          слой         слой

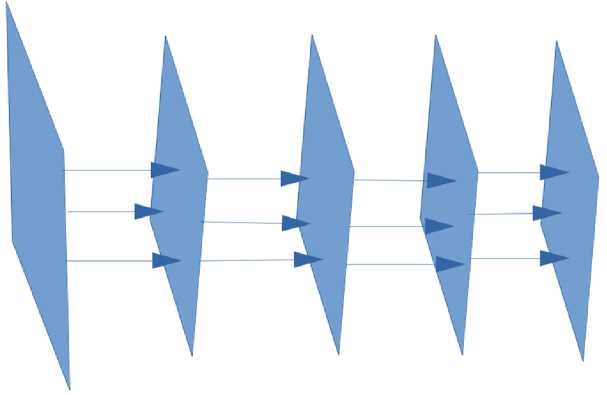
Количество нейронов       20       LSTM 256      LSTM 256       Relu 32     Linear 32

Рисунок 2 – Строение нейронной сети

На вход нейронной сети подается матрица размерностью 20 × 6, далее значения передаются на рекуррентный слой, который состоит из 256 нейронов рекуррентной нейронной сети, далее процедура повторяется и по окончании результаты агрегируются слоем прямого распространения с функцией активации Relu [10]. Конечный результат поступает на выходной слой с одним нейроном и линейной функцией активации.

Для создания нейронной сети воспользуемся языком программирования Python, а также библиотеками для обработки и визуализации данных:

– pandas;

– numpy;

– matplotlib;

– keras (в качестве основы tensorflow);

– sklearn.

В качестве функции потерь в процессе обучения используется среднеквадратическая ошибка (Mean Squared Error), оптимизация осуществляется с использованием алгоритма Adam [11]. Обучение производится итеративно в течение 10 эпох для отслеживания возможного переобучения (рис. 3).

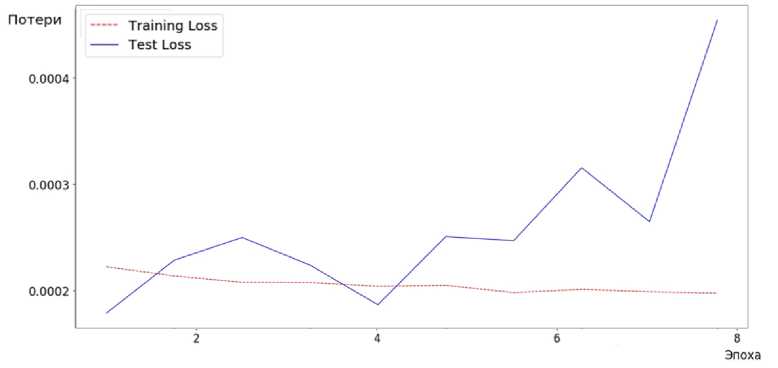
Рисунок 3 – Изменение ошибки на тестовой и проверочной выборке

Как можно заметить, потери тестовой выборки возрастают после первой эпохи, в которой наблюдается минимальное значение ошибки. Также можно заметить монотонное убывание ошибки тренировочных данных, что при сопоставлении всей полученной информации означает, что модель начинает переобучаться на основании тренировочных данных. Таким образом, для получения наилучшего результата воспользуемся моделью с первой эпохи.

После обучения получаем следующие значения ошибок:

– Train Score: 0.00002 MSE;

– Test Score: 0.00036 MSE.

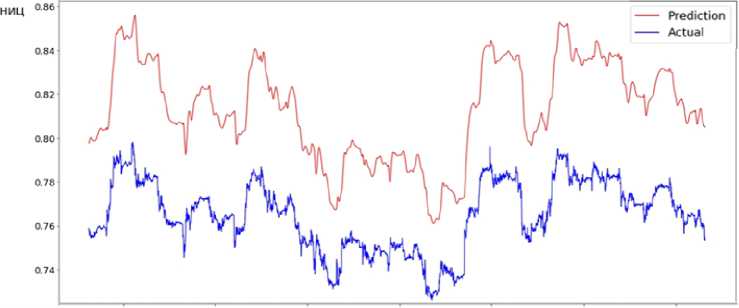
Визуализируем прогнозируемое нормализованное изменение цены (НИЦ) на месячном временном отрезке (отложенном на основе 5-минутных интервалов), а также сравним их динамику с нормализованными историческими движениями финансового инструмента (рис. 4).

500             1000            1500            2000            2500            3000            3500

Временной интервал

Рисунок 4 – Сравнение прогнозируемых показателей и исторических данных

При анализе рисунка 4 можно заметить, что прогностическая кривая отображает динамику поведения финансового актива. Несмотря на то что линия прогноза (верхняя кривая) является более сглаженной, она повторяет изменение цены, что в свою очередь означает: рекуррентные нейронные сети могут прогнозировать поведение рыночных активов. Уровни ошибки на тренировочной и валидационной выборке показывают, что модель несколько хуже прогнозирует реальные данные, это может быть обусловлено изменяющимися процессами в отложенных данных. В то же время усложнение модели и создание агрегирующих слоев позволяет не использовать большие мощности для оптимизации на 250 или 500 эпохах.

Также можно выделить некоторые недостатки данной модели:

• –    во время обучения сложно трактовать результаты, это накладывает ограничения на возможность улучшения модели;

• –    невозможно предсказать, когда изменится динамика рынка и модель перестанет работать;

• –    каждому отдельному инструменту соответствует натренированная на его данных модель, использование других моделей снижает эффективность прогнозирования.

Построенная модель может быть использована как для решения задач риск-менеджмента (для регуляризации резервного капитала по отдельному инструменту), так и для выполнения краткосрочных финансовых операций.

IEEE Transactions on Neural Networks and Learning Systems

Ссылки:

• 1.    Semantic Object Parsing with Graph LSTM / Xiaodan Liang [et al.] // Proceedings ECCV 2016. Pt. I / ed. by B. Leibe [et al.]. Cham, 2016. P. 125–143.

• 2.    Application of Pretrained Deep Neural Networks to Large Vocabulary Speech Recognition / N. Jaitly [et al.] // Proceedings of Interspeech. 2012.

• 3.    Making Deep Belief Networks Effective for Large Vocabulary Continuous Speech Recognition / T.N. Sainath [et al.] // Automatic Speech Recognition and Understanding. 2011. P. 30–35.

• 4.    DeepFace: Closing the Gap to Human-Level Performance in Face Verification / Y. Taigman et al. // Proceedings 2014 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC, 2014. P. 1701–1708.

• 5.    Karpathy A. The Unreasonable Effectiveness of Recurrent Neural Networks [Электронный ресурс]. 2015. URL: http://kar-pathy.github.io/2015/05/21/rnn-effectiveness/ (дата обращения: 27.05.2018).

• 6.    LSTM: A Search Space Odyssey [Электронный ресурс] / K. Greff [et al.] // IEEE Transactions on Neural Networks and Learning Systems. 2017. Vol. 28, no. 10. P. 2222–2232.

• 7.    Roondiwala M., Patel H., Varma S. Predicting stock prices using LSTM / // International Journal of Science and Research. 2017. Vol. 6, no. 4. P. 1754–1756.

• 8.    Hansson M. On stock return prediction with LSTM networks // Lund University, 2017.

• 9.    Sklearn.preprocessing.MinMaxScaler [Электронный ресурс]. URL:    http://scikit-learn.org/stable/modules/gener-

  ated/sklearn.preprocessing.MinMaxScaler.html (дата обращения: 27.05.2018).

• 10.    Glorot X., Bordes A., Bengio Y. Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics [Электронный ресурс]. 2011. URL: http://proceedings.mlr.press/v15/glorot11a.html (дата обращения: 27.05.2018).

• 11.    Kingma D.P., Lei Ba J. Adam:  A Method for Stochastic Optimization [Электронный ресурс]. URL:

(дата обращения: 27.05.2018).