Прогнозирование физико-механических свойств пряжи с вложением полипропиленовых волокон

Проблема прогнозирования свойств текстильных материалов, полученных из различных видов исходного сырья, является одним из наиболее популярных направлений в текстильной науке. Наибольшие успехи в данном направлении достигнуты в разработке методов прогнозирования относительной разрывной нагрузки пряжи. Однако до настоящего времени не создано общей теории, позволяющей с высокой точностью осуществлять расчет физико-механических свойств пряжи с учетом свойств текстильных волокон и режимов их переработки.

Известно, что традиционные методики прогнозирования разрывной нагрузки пряжи из неоднородных волокон строились на основе анализа экспериментальных данных и имели множество ограничений по их применению. В случае использования известных методик для прогнозирования прочности пряжи с вложением полипропиленовых (ПП) волокон существенным фактором, снижающим точность расчета, является повышенное значение разрывного удлинения полипропиленового волокна, которое составляет более 80 % и значительно превышает значение удлинения химических волокон, традиционно перерабатываемых в смесях с хлопком в период разработки данных методик.

Так расчет по формуле профессора А.Н. Ванчикова показал, что относительная разрывная нагрузка хлопкополипропиленовой пряжи (70 % хлопок / 30 % ПП волокно) прогнозируется на уровне 9,8 сН/текс. В то же время экспериментальные исследования показали, что фактическое значение данного показателя находится в пределах 11,5 – 12 сН/текс. Таким образом, погрешность получаемых результатов расчетов по данной формуле превышает 15 %.

Кроме того, можно отметить, что в настоящее время также отсутствуют общепринятые методики для прогнозирования разрывного удлинения пряжи и неровноты пряжи по свойствам. Только профессором А.Н. Соловьевым получена полуэмпирическая формула для расчета неровноты хлопчатобумажной пряжи по разрывной нагрузке [1]. Однако эта формула не может быть использована только для расчета неровноты по прочности смесовой пряжи.

Разработка новой методики осуществлялась на основе положений, описанных в [2]. Согласно данной методике, для расчета относительной разрывной нагрузки двухкомпонентной пряжи должны выполняться следующие этапы:

• 1.    Определение линейной плотности наиболее слабого участка пряжи.

• 2.    Расчет крутки на рассматриваемом участке.

• 3.    Определение количества волокон каждого компонента в сечении пряжи по формуле.

• 4.    Расчет диаметра пряжи.

• 5.    Расчет длины скольжения волокон более растяжимого компонента при разрыве волокон менее растяжимого компонента.

• 6.    Расчет суммарной прочности волокон каждого компонента с учетом наличия ворсинок и проскальзывающих волокон.

• 7.    Расчет прочности волокон в сечении пряжи при разрыве волокон малорастяжимого компонента.

• 8.    Определение разрывной нагрузки пряжи на основе сопоставления разрывной нагрузки волокон высокорастяжимого компонента и нагрузки, приложенной к пряже в момент разрыва волокон малорастяжимого компонента.

Анализ данной методики, рассматриваемой в качестве базовой, выявил ряд ее недостатков:

• –    в модели включен ряд характеристик, которые не могут быть определены с достаточной точностью с использованием наиболее распространенного лабораторного оборудования; например, средняя длина ворсинки и неровнота пряжи на отрезках длиной 50 см;

• –    в существующей методике не учитывается влияние неровномерности смешивания компонентов на крутку участка пряжи и его прочность;

• – базовая методика не позволяет прогнозировать другие физикомеханические свойства пряжи кроме ее относительной разрывной нагрузки;

  – при выводе формулы для расчета коэффициента укрутки участка в момент разрыва для упрощения принято допущение о том, что в области сечения пряжи, находящейся вблизи ее оси, растяжение волокон не происходит (то есть гофрированные волокна распрямляются, но не удлиняются). Однако данное допущение в ряде случаев приводит к высокой погрешности получаемых результатов.

Для устранения указанных недостатков в разрабатываемую методику прогнозирования были внесены следующие корректировки.

Для получения более полной информации в усовершенствованной методике моделируется процесс растяжения до разрыва некоторого количества образцов пряжи (не более 50). Каждый моделируемый образец пряжи разделен на некоторое заданное количество участков, в каждом из которых рассматривается по одному сечению.

Растяжение каждого участка рассматривается независимо друг от друга, а затем строится обобщенная кривая растяжения образца в целом с учетом перераспределения удлинений участков в моменты разрыва волокон в каждом из них. Необходимо также отметить, что для получения возможности учета неровномерности волокон по свойствам в процессе моделирование определяется изменение свойств пряжи в моменты разрыва каждого волокна в любом из рассматриваемых сечений пряжи.

Для определения линейной плотности каждого из участков необходима информация о неровноте пряжи по линейной плотности на коротких отрезках (1 см) и отрезках длиной 50 см. Однако последняя характеристика не может быть указана в таблицах, получаемых на современных приборах для оценки неровноты пряжи (например, UsterTester), а определение ее по градиенту неровноты не обеспечивает высокой точности результатов.

Поэтому для определения неровноты пряжи на отрезках длиной 50 см можно рекомендовать использование информации на отрезках длиной 1 см и 1 м.

Известно, что для продуктов со случайной неровнотой значение С V (L i ) уменьшается с увеличением длины отрезка L i . Для построения градиентов неровноты по линейной плотности продуктов прядения пользуются формулами Брени. Можно показать, что если продукт образован из волокон одинаковой длины и линейной плотности, и волокна в продукте расположены случайно (модель Мартиндайля), то квадратическая неровнота по массе отрезка определяется как [3]

C V (L)

C v (0) •

l

L  3 ( L )

если l <  L <да ,

где l – средневзвешенная длина волокон в пряже, мм.

Cv (0) – квадратическая неровнота по линейной плотности обрезков при L → 0, %

Однако реальная форма градиента внешней неровноты существенно отличается от идеальной. При разработке модели было принято допущение о следующем характере зависимости неровноты по линейной плотности пряжи от длины отрезка:

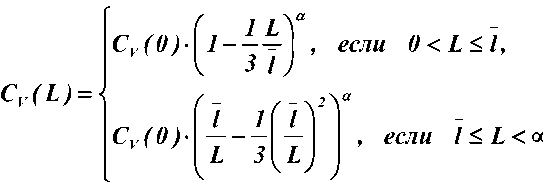
C v (L) = 1

C v (0) •U

C v (0) •

к

L 3 к L )

l

—- I , если 0 <  L <  l 3 l )

)

если l <  L < да .

В результате преобразований получена следующая зависимость:

x a

Cy (50см ) = Су (1см ) •

l

50 - 500/- к / 3l )

где a - показатель степени, рассчитываемый по формуле

(       _ X a =

1000 - 10000/ к 3l

In ( C_v(1 м )/ C_v(1cm ) ) ’

Таким образом, на основании информации о параметрах неровноты пряжи, определяемых с использованием прибора UsterTester, по формуле (3) можно рассчитать неровноту пряжи на отрезках, длина которых равна зажимной длине на разрывной машине (50 см), а затем осуществить генерацию ряда случайных чисел, соответствующих средней линейной плотности каждого моделируемого образца пряжи.

Аналогично определение линейной плотности каждого исследуемого сечения каждого образца можно осуществлять, в результате моделирования с учетом внутренней неровноты пряжи на отрезках длиной 50 см, определяемой как V С²(1см) - С²(50см) .

Полученные таким образом значения линейной плотности пряжи распределены по нормальному закону распределения, принимаемому по умолчанию. Однако для реальной пряжи характерна асимметрия распределения масс отрезков. Для пряжи кольцевого способа прядения отклонения линейной плотности отрезка в большую сторону от среднего значения в 1,2 – 2 раза превышают отклонения в меньшую сторону (рис. 1).

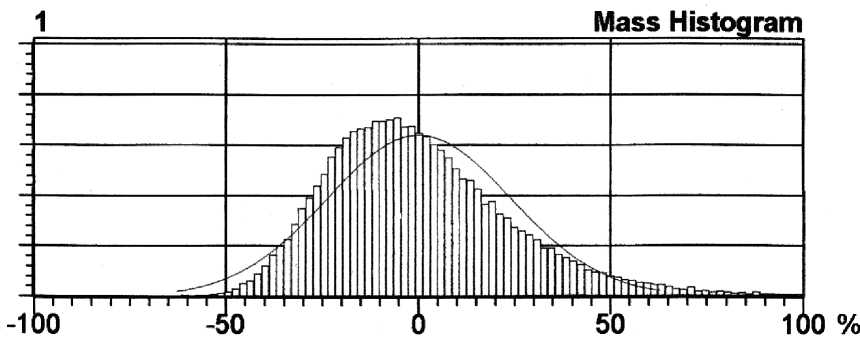
Рисунок 1 – Гистограмма распределения отклонений масс отрезков хлопкополипропиленовой пряжи линейной плотности 20 текс (80 % хлопок / 20 % ПП волокно) от среднего значения, полученная с использованием прибора Uster

Tester 5

Для учета влияния этого явления на свойства пряжи после генерирования значений линейной плотности участков пряжи осуществляется их корректировка по следующим формулам:

T j = (T' j - T n )a + + Т п , если T >  Т п ,                    (6)

T = (TV - T n )a _ + Т п , если T <  T n ,                   (7)

где T’ – линейная плотность участка пряжи, рассчитанная с учетом полученного в результате моделирования количества волокон в сечении, текс; ТП – средняя линейная плотность пряжи, текс, a+ и а- – поправочные коэффициенты, рассчитываемые по формулам a+

2k k +1’

a —------,

- k +1, где k – показатель, характеризующий асимметрию гистограммы распределения масс отрезков.

Линейная плотность участка пряжи оказывает существенное влияние как на суммарную прочность волокон в рассматриваемом сечении, так и на значение крутки. Однако необходимо обратить внимание на то, что в сечении смешанной пряжи находятся волокна, обладающие различными геометрическими и механическими свойствами, что также оказывает влияние на перераспределение крутки между разными сечениями пряжи.

При разработке методики принимаем, что крутка участка пряжи вблизи рассматриваемого сечения зависит от жесткости пряжи на данном участке следующим образом:

Kj — KG’ j       _Gj

где K - средняя крутка пряжи, кр./м, G и G j - соответственно, средняя жёсткость при кручении пряжи и рассматриваемого участка j , Н м².

При расчете жесткости пряжи в сечении рассматриваемого участка учитывается фактическое процентное содержание и характеристики волокон каждого из компонентов.

Вместо значения средней длины ворсинки целесообразно использовать показатель относительной ворсистости Н , определяемый на приборе UsterTester, и соответствующий суммарной длине ворсинок, выраженной в сантиметрах, приходящейся на 1 см длины пряжи.

Ориентировочные сведения о значении показателя Н содержатся в бюллетене Uster Statistics. Зная значение этого показателя, можно рассчитать количество волокон в теле пряжи (на участке вокруг j-того сечения) по уточненной формуле

n Тj

— n ПР

1

НТв )

к

Т

Т п 7

,

где T В – линейная плотность волокна, текс; H j – ворсистость в моделируемом сечении пряжи, зависящая от средней ворсистости пряжи H и линейной плотности T j участка j , в который попадает рассматриваемое сечение:

T я, — н^-. J         гр

Как указывалось выше, в базовой методике при их выводе формул для расчета укрутки пряжи в процессе разрыва допускалось, что в области сечения пряжи, находящейся вблизи ее оси, растяжение волокон не происходит. Однако применение данного допущения в ряде случаев не является оправданным и ведет к возникновению существенных погрешностей получаемых результатов.

Для уточнения ранее применяемых формул воспользуемся выражением для расчета среднего удлинения волокон в сечении пряжи в процессе ее растяжения, приведенной в [1]:

^р = 6r²У2^!К^{! (} 1 ^{+ ( 2 n} Krn^ -^ ^{+ ( 2 n K}r H ) )  - ^{1 +} 7" ,

где r П – радиус пряжи, мм; К – крутка пряжи, кр./м; К У – коэффициент укрутки; r Н – радиус нейтрального слоя пряжи, мм.

Тогда в момент разрыва удлинение волокон можно рассчитать по формуле р р —

KУР бгПпК Р 2

( 1 + ( 2 п К р Гп ) ² ) 3/2 — ( 1 + ( 2 п К р н ) ² ) 2

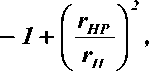
где К Р , К УР , r НР – соответственно, крутка пряжи, коэффициент укрутки и радиус нейтрального слоя в момент разрыва.

Крутка участка пряжи К Р в момент разрыва связана с круткой К , сообщаемой рассматриваемому участку пряжи в процессе ее формирования, следующим соотношением:

K Р

K_У — К.

K УР

В случае разрыва пряжи, происходящего при растяжении всех волокон в слабом сечении, то есть радиус нейтрального слоя равен 0 (нейтральный слой отсутствует), а коэффициент укрутки при разрыве КУР больше 1, формула (14) принимает вид рР — Л 2K У2К 2 [(1 + (2пКР ГП )2 )3 /2 - 11- 1.          (17)

6ГПП K Р L                     -1

После преобразований выражения (17) получаем, что при условии К УР >  1 среднее удлинение волокон в момент разрыва может быть рассчитано по формуле

р — 2К Ур

^Р 3yK У²

КУр

V

+

УК У ) ^{/ 2}

K

УР )

— 1

- 1,

где

У — (2пКгп )2 — tg2в ,

β – угол наклона волокна на поверхности пряжи к ее оси.

Однако разрыв может произойти и при условии К УР <  1 . В этом случае наличие нейтрального слоя должно учитываться при расчете удлинения волокон.

Радиус нейтрального слоя пряжи при формировании рассчитывается по формуле rH =

-j 1 - кУ

2 • п-К • К У

Однако в процессе растяжения пряжи для случая, когда К УР <  1 , радиус нейтрального слоя уменьшается в диапазоне от r Н до 0 .

Для определения радиуса нейтрального слоя в момент разрыва необходимо учесть изменение крутки и коэффициента укрутки, произошедшие вследствие растяжения пряжи:

гнр =

У1 - кУр

2 • п • К _Р • К_УР

В результате подстановок и преобразований установлено, что при К_УР <  1 удлинение волокон при разрыве может быть рассчитано по следующей формуле:

^Р 3yK У²

' 1 + ^yKy' к²

^K У³Р

+-----ГР" • yKУ2

При КУР = 1 формулы (18) и (22) принимают одинаковый вид рр =

Полученные формулы используются в разрабатываемой методике для расчета коэффициента укрутки участка пряжи при достижении одним или несколькими волокнами разрывного удлинения.

Расчетное значение коэффициента укрутки используется для определения длины скольжения неразорвавшихся волокон одного или нескольких волокон в рассматриваемом сечении:

2 • п- ft-К р • 1	K УР2	K У4P
	( £ р + 1)	( Р р + 1)

,

где f i – коэффициент трения волокон i-того компонента.

Расчет нагрузки, приложенной к пряже при разрыве каждого из волокон в любом из рассматриваемых сечений, осуществляется согласно формулам базовой методики, приведенным в [1]. Разрывной нагрузкой пряжи считается приложенная нагрузка, которая оказывается больше суммарной прочности всех неразорвавшихся волокон в наиболее слабом ее сечении.

Относительное удлинение каждого рассматриваемого ( i -того) участка пряжи, %, рассчитывается по формуле

pi =