Прогнозирование энергетических характеристик непрерывного кислородно-иодного лазера с разными типами накачки

Создание мощных источников лазерного излучения является крупной научной проблемой, над решением которой работает большое число ученых во всем мире. Любой лазер по определению является преобразователем энергии какого-либо вида (энергии накачки) в энергию когерентного излучения оптического диапазона. Важнейшей характеристикой мощных лазеров является коэффициент такого преобразования. В отличие от технических устройств, где подобный параметр называют коэффициентом полезного действия, в лазерной физике используют понятие энергетической эффективности. В определении энергетической эффективности в качестве затраченной энергии фигурирует только величина энергии накачки без учета энергозатрат на работу вспомогательных систем и устройств.

Непрерывный кислородно-иодный лазер (КИЛ) является самым мощным источником когерентного излучения на сегодняшний день. По типу накачки непрерывные КИЛ делятся на химические и электроразрядные. В настоящее время энергетическая эффективность химического КИЛ (ХКИЛ) увеличена до теоретического предела [1]. Создан [2] и успешно совершенствуется электроразрядный кислородно-иодный лазер (ЭКИЛ) [3]. Для повышения выходных параметров газовых лазеров модным трендом является применение оптической накачки [4–7]. Предпо-

лагается, что такая накачка будет эффективной и для непрерывного КИЛ. Кислородно-иодный лазер с оптической накачкой (ОКИЛ) впервые был предложен в [8]. Концепция оптического КИЛ на примере одной из схем развита Загидул-линым М.В. [9].

Энергетическая эффективность η непрерывного КИЛ определяется как отношение выходной мощности Wout к максимально возможной мощности Wp или как отношение числа лазерных фотонов, излученных в единицу времени, к числу молекул энергоносителя, израсходован- ных за это время:

W_p hv Gq^

где h ν – энергия фотона, излученного на лазерном переходе I(²P_1/2, F=3) → I(²P_3/2, F’=4) . Здесь в знаменателе используется расход кислорода, чтобы обеспечить рассмотрение лазеров с различными типами накачки с единых позиций, поскольку молекулой-энергоносителем во всех непрерывных КИЛ является синглетный кислород O₂(¹∆) . Для химического лазера энергетическая эффективность будет незначительно отличаться, поскольку в цепочке преобразований исходно участвуют молекулы хлора. Однако в современных генераторах степень переработки хлора в кислород в химической реакции близка к 100 %.

К настоящему времени развиты численные модели, позволяющие решать задачи прогнозирования выходных характеристик (мощности, энергетической эффективности) в трехмерной постановке с учетом кинетики процессов в активной среде, газовой динамики, а также полезных и паразитных оптических потерь [10, 11]. Однако условия работы непрерывного КИЛ по- зволяют ввести ряд допущений, существенно упрощающих математический формализм, в частности, рассматривать случай одномерного течения [12].

Здесь применяется упрощенная двухуровневая модель генерации, развитая для расчета выходных характеристик непрерывного КИЛ без учета кинетических потерь в [13] и с учетом наиболее быстрых релаксационных процессов в [14]. В работе [15] предложено трехмерное представление режимов работы непрерывных КИЛ с использованием критериев подобия. На этой основе в [16] разработан метод картирования выходных характеристик кислородно-иодных лазеров, позволяющий спрогнозировать параметры, при которых реализуются режимы работы с высокой энергетической эффективностью. Однако для получения полной картины требуется определение максимальной длины области усиления в направлении потока, до которой еще возможна генерация. Упрощенная расчетная модель берется за основу, поскольку в нее включены только наиболее значимые потери. По этой причине именно она устанавливает теоретический предел энергетической эффективности и позволяет проводить качественный анализ влияния наиболее характерных процессов.

Целями настоящей работы являются усовершенствование метода картирования режимов генерации непрерывных КИЛ с различными типами накачки с использованием нормированных значений критериев подобия, создание метода оценки предельной энергетической эффективности непрерывных КИЛ, а также демонстрация практической применимости обоих методов.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

В непрерывном КИЛ в резонатор поступает газовый поток, содержащий молекулы энергоносителя – синглетного кислорода O₂(¹∆) , атомы и молекулы йода, частицы несущего буферного газа и тушащие компоненты. Полагаем, что смешение кислородного и йодного потоков происходит мгновенно в узле смешения. Принимаем, что имеет место неполная диссоциация молекул йода, которая завершается до входа в резонатор. Таким образом, газодинамические параметры потока и концентрации компонентов в области генерации остаются постоянными. Считаем вну-трирезонаторную интенсивность постоянной во всем объеме, занятом излучением, и насыщение контура усиления однородным, что справедливо для лазеров с широкоапертурными устойчивыми резонаторами [14–16]. В настоящей работе, как и в [16] рассматриваем только процессы, происходящие в резонаторе, т. е. исключаем диссоциацию из модели. Считаем, что кинетика активной среды определяется реакцией накачки

и релаксационными процессами, в которых происходит тушение возбужденного состояния атома йода

,(3)

,(4)

I^P^ + ^C^) "> Ч^2рз/2) + ^О)

->'( ^/zj + ^C¹^

Константа равновесия процесса (2) определяется выражением K _e= k_f / k_r =0,75×exp(401,4⁄ T ); k_f =5,12×10^-12 T ^0,5 см³/c – константа скорости прямой реакции; k_r – константа скорости обратной реакции; T – температура газа, K. Константы скоростей процессов (3) и (4) соответственно равны k ₃=2,0×10^-12 см³/c, k ₄=3,8×10^-11 см³/c [14–16]. Значение константы скорости процесса (5) измерено в работе [17] и составляет k ₅=4,2×10^-13 см³/c. В активной среде ЭКИЛ пары воды отсутствуют, но она содержит атомы кислорода, эффективно тушащие возбужденные атомы йода в процессе (6). Константа скорости последнего составляет k ₆=6,5×10^-12( T /300)^1,76 см³/с.

Ниже для непрерывного КИЛ рассматриваем три основных параметра: эффективность извлечения энергии из активной среды n extm , параметр х и энергетическую эффективность п [14–16]. Первый определяет долю молекул синглетного кислорода, энергия которых переведе-

на в излучение и = У — Л У — У

.

Здесь Y_i – доля синглетного кислорода на входе в резонатор, ∆ Y _relax – потери O₂(¹∆) за счет релаксационных процессов, Y_d – доля синглетного кис-

лорода на выходе резонатора.

Параметр х показывает, какая часть энергии молекул синглетного кислорода, доступной для перевода в излучение, была фактически переведена в него в активной среде [18]

X -

^2^5^ Vi-Y_TH

lextm ₌ 1 _ ^тек^^оиГ

Yi-YTH

Yi-YTH

. (8)

Величина ∆Y_out = Y_d – Y_TH характеризует потери молекул энергоносителя, не задействованных в процессе генерации, так называемые потери «на вынос», Y_TH =(2 K _e+1)^-1 – пороговая доля синглетного кислорода. Выражение (8) свидетельствует, что 100%-ную эффективность можно получить, только сведя к нулю потери в резонаторе.

Согласно [14–16], энергетическую эффективность можно представить в виде

, (9) где n _extr= t r /( t _r+ a ) - доля лучистой энергии, выводимая из резонатора, или эффективность резонатора ( t _r - суммарное пропускание зеркал, a -коэффициент потерь на зеркалах).

Как показано в [14-16], энергетические характеристики непрерывного КИЛ могут быть найдены с использованием системы уравнений:

dy         2    (1-ЗУ_гн)У+2У_тн + (1-У_тн)(Л+ЗС/2)^,( )

=                ~               ~        (П)

d 1        2П               2П при начальном условии У|y=0=Yi. В уравнениях (10) и (11): У - доля синглетного кислорода; Y=(2 к[ 1] о t)/[3(1- YTH)] - безразмерное время, характеризующее процесс перевода энергии синглетного кислорода в излучение при бесконечно большой интенсивности поля в резонаторе ([ 1]о - полная концентрация атомарного йода, t=x/и - время пребывания газовой смеси в зоне генерации, отсчитываемое от момента входа, x - расстояние в направлении потока от начала резонатора, и - скорость потока); Л=(к[О]+ +к4[I2]+к5[02(1 А)])/(к[02]о) - критерий, выражающий отношение скоростей релаксации и возбуждения для электронно-возбужденных атомов йода (константа скорости к и концентрация [О] - к=к3 и [ Q]=[H2 0] для ХКИЛ и ОКИЛ, к=к6 и [ Q]=[0] для ЭКИЛ; [I2], [02(1 А)] - концентрации молекул йода и синглетного кислорода в резонаторе; [02]о - полная концентрация молекул кислорода); C=стJ/(hvк[02]о) - нормированная внутрирезо-наторная интенсивность (ст - сечение вынужденного излучения/поглощения для доплеровски уширенного перехода I(2P1/2, F=5)^I(2P3/2, F=4), определяемое выражением ct=1,3x10-16Го,5 см2; J - внутрирезонаторная интенсивность излучения, циркулирующего в обоих направлениях); Yd=2к[I]оtd/[3(1- YTH)] - критерий, выражающий безразмерное время, за которое доля синглетного кислорода доступная для извлечения в активной среде уменьшается в e раз при бесконечно большой интенсивности поля в резонаторе (t=d/и - полное время пребывания газа в зоне генерации, d - размер области, занятой излучением на зеркале, в направлении потока); П=2ст[I]0L/(tr+а) - превышение максимального усиления над потерями (L - длина усиления). В [14] показано, что эффективность извлечения энергии из активной среды определяется вторым членом в правой части (11), третий член в правой части (11) устанавливает значение релаксационных потерь.

Используя выражение для расчета доли синглетного кислорода на выходе резонатора, полученное в неявном виде в [14], можно показать, что генерация по потоку сохраняется до координаты y _d ^ma , определяемой при решении трансцендентного уравнения

(П — 1 + ЗГТЯ)(1 - ¥тн)ЛуГх - П[2ГТЯ +

" ^л L      * т я JJ *^п ;                  ^{= 12} ■(^

Принимая во внимание определения n _extr и параметра П , получаем [15]

= 1 . (13)

“max где Птах=2ст[I]0L/а. Т. е. с ростом отношения усиления к величине оптических потерь эффективность резонатора уменьшается при фиксированном максимальном превышении усиления над потерями, которое достигается в случае закрытого резонатора.

Таким образом, при картировании режимов по методике, изложенной в [16], введение кинетических и оптических потерь в расчетную модель позволяет ограничить область определения выходных характеристик по координатным осям величинами у d ^max и П _max.

В [13,14] приведены результаты анализа целого ряда работ, свидетельствующие о том, что эффективность резонатора может превышать 90 %, а в некоторых случаях близка к единице. Следовательно, для оценки выходных характеристик с учетом (9), можно принять п ~ П^ -Авторами [14] показано, что при реализации высоких превышений ( П ^8) эффективность извлечения энергии из активной среды отличается от максимальной не более, чем на 2-3 % при произвольной длине резонатора по потоку.

Математическая модель для расчета выходных характеристик непрерывного КИЛ с учетом потерь, разработанная в [14-16], позволяет получить следующую формулу для определения максимальной эффективности извлечения энергии из активной среды в приближении сильного поля ( П ^ “ ) в случае резонатора конечной длины ( Y _d )

ti =(Г,-1'„)(1-е->-0-

— _ — .            -.             (14)

Зависимость (14) характеризуется наличием экстремума

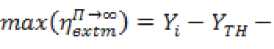
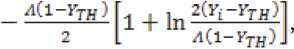
который достигается для резонатора длиной по

, 2(У;-УТд) у = [□---1---1^3—

потоку

•

Тогда превышение, соответствующее максимуму энергетической эффективности, можно вычислить в приближении сильного поля, пода- вляющего потери,_по формуле

^ _ (1-ЗУ_Тн)»7^”-ЗУ_тя(1-У_тя )1п(1-х)

7?ыгГт[1+^1п(1-^]

. (17)

Следовательно, максимальная оценочная энергетическая эффективность непрерывного КИЛ составляет п ” n _extm( Y d , П ), где величины n _extm, Y d и П определяются по формулам (15), (16) и

• (17 ) соответственно. При этом в качестве исходных данных необходимы только начальная Y_i и пороговая Y_TH доли синглетного кислорода и значение критерия Λ , которые, как правило, приближенно известны до проведения экспериментов. В этом и состоит суть предлагаемого метода упрощенной оценки предельных выходных характеристик непрерывных КИЛ.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

В настоящей работе рассматриваются режимы генерации непрерывных КИЛ, в которых достигается высокая эффективность преобразования энергии накачки в энергию лазерного излучения. По этой причине в последующих расчетах будут использованы параметры, характеризующие режимы работы наиболее совершенных лазеров – ХКИЛ [1], ЭКИЛ [3], указанные в табл. 1 в [14], и ОКИЛ [9]. Исключение составляют потери на зеркалах α для ЭКИЛ [3]. Здесь, как и в работе [15], эта величина принята равной 0,1 t_r , что характерно для большинства экспериментальных работ с непрерывным КИЛ. Такое допущение позволяет провести адекватное сравнение лазеров с накачкой всех трех типов. Для ЭКИЛ рассматривается только первый резонатор (см. работу [3]). Геометрию резонатора ОКИЛ [9] считаем аналогичной геометрии первого резонатора в работе [3], поскольку параметры потока в этих работах близки. В табл. 1 представлены параметры, фигурирующие в качестве исходных данных в расчетах выходных характеристик непрерывных КИЛ с химической [1], электроразрядной [3] и оптической [9] накачкой. Они соответствуют величинам, приведенным в табл. 1 и 2 в работе [16]. Значения параметра γ _d ^max определены с использованием уравнения (12) и округлены.

В работах [15, 16] для непрерывных КИЛ обоснована актуальность представления эффективности извлечения энергии из активной среды ηextm, параметра χ и энергетической эффективности η как функций безразмерных критериев подобия γd и ∏, выступающих в роли независимых аргументов. Критерий γd устанавливает, достаточное ли время газовая смесь находится в резонаторе для перевода запасенной в активной среде энергии в излучение. Критерий ∏ определяет максимальный уровень усиления оптического сигнала в активной среде при многократных переотражениях от зеркал. При отсутствии кинетических и оптических потерь возможно достижение предельной энергетической эффективности, соответствующей эффективности извлечения энергии из активной среды ηextm=Yi–YTH [19]. Учет кинетических и оптических потерь, определяемых значениями Λ и ∏max, приводит к ограничению областей определения функций ηextm, χ и η конечными интервалами. Ненулевое Λ имеет следствием появление максимумов на поверхностях рассматриваемых параметров в направлении газового потока (ось γd), а конечное ∏max (α≠0) дополнительно приводит к экстремуму η по оси второго аргумента.

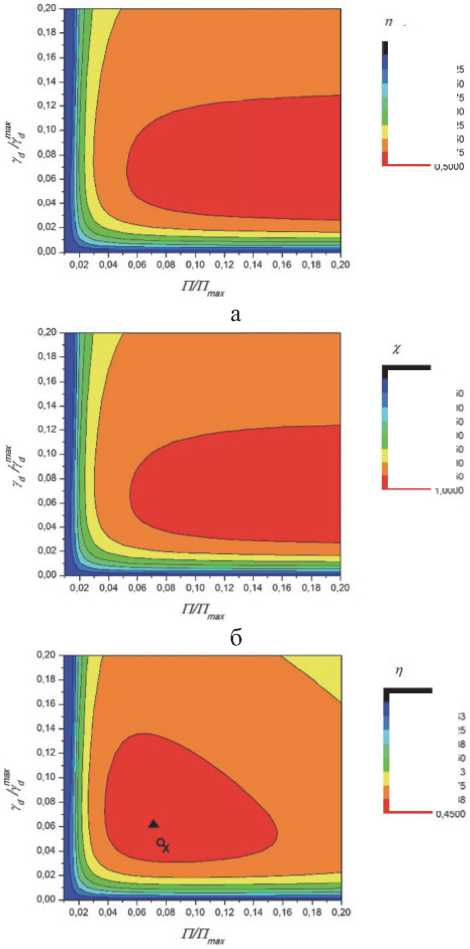
На рис. 1–3 приведены зависимости параметров η _extm, χ и η для непрерывных КИЛ как функций критериев подобия γ _d и ∏ в нормированных координатах для лазеров с химической [1], электроразрядной [3] и оптической [9] накачкой, полученные на основе параметров, указанных в табл. 1. Эффективные режимы генерации реализуются при значениях координат γ _d/ γ _d ^max и ∏/∏_max , соответствующих красным областям на графиках. Наиболее высокая энергетическая эффективность достигается для лазеров с химической накачкой, что обусловлено приблизительно в 5 раз более высоким значением доли O₂(¹∆) на выходе генератора синглетного кислорода. При этом для непрерывных КИЛ с накачкой всех трех типов может быть достигнута высокая ( χ >90 %) степень преобразования энергии в активной среде. Расчеты подтверждают прогнозируемое положение, что введение в рассмотрение кинетических и оптических потерь ограничивает область эффективных режимов генерации в направлениях обеих координатных осей. Таким образом, картина представления режимов генерации при моделировании с учетом потерь становится более реалистичной, поскольку очевидно, что оптимальный вывод излучения достигается не в случае «глухого» резонатора бесконечной длины в направлении потока. Кроме того, вместо монотонного роста η при увеличении значений γ _d и ∏ , на поверхности η = f ( γ _d , ∏) наблюдается одиночный экстремум.

Метод картирования при включении в расчетные уравнения наиболее скоростных релаксационных процессов и паразитных потерь на зеркалах позволяет не только описывать реализованные режимы генерации, но и прогнозировать размерные параметры, при которых достигаются максимальные выходные характеристики. В табл. 2 приведены данные, позволяющие определять положения максимумов на дву-

Таблица 1. Исходные данные для расчета выходных характеристик непрерывных КИЛ

Y t	YTH	Л	max Y d	^ max	Работа
0,64	0,14	0,011	100,0	100,0	[1]
0,13	0,03	0,003	75,0	120,0	[3]
0,11	0,01	0,004	50,0	1000,0	[9]

мерных графиках (рис. 1,в, рис. 2,в и рис. 3,в) и соответствующие им значения энергетической эффективности. Значение η для химического КИЛ [1] пересчитано с учетом определения (1).

Анализ двумерных зависимостей и данных табл. 2, позволяет сделать следующие выводы. Положение максимума в направлении вертикальной оси приблизительно одинаково для лазеров с накачкой всех трех типов. По второй координате максимумы энергетической эффективности для ХКИЛ [1] и ЭКИЛ [3] также расположены достаточно близко. Высокое значение ∏max для ОКИЛ [9] обусловлено, в первую очередь, высокой концентрацией атомов йода [I]0=2×1015 см-3 и экстремально низкой температурой потока T=86 K. Поскольку, как показано

в

Рис. 1. Зависимости выходных характеристик непрерывного ХКИЛ [1]: а – эффективности извлечения энергии из активной среды η _extm, б – параметра χ , в – энергетической эффективности η как функции критериев подобия γ _d и ∏ в нормированных координатах.

Обозначения символов на рис. 1, в: ▲ - наиболее эффективный расчетный режим генерации, × – экспериментальное значение, ○ – оценочное значение

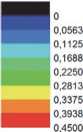
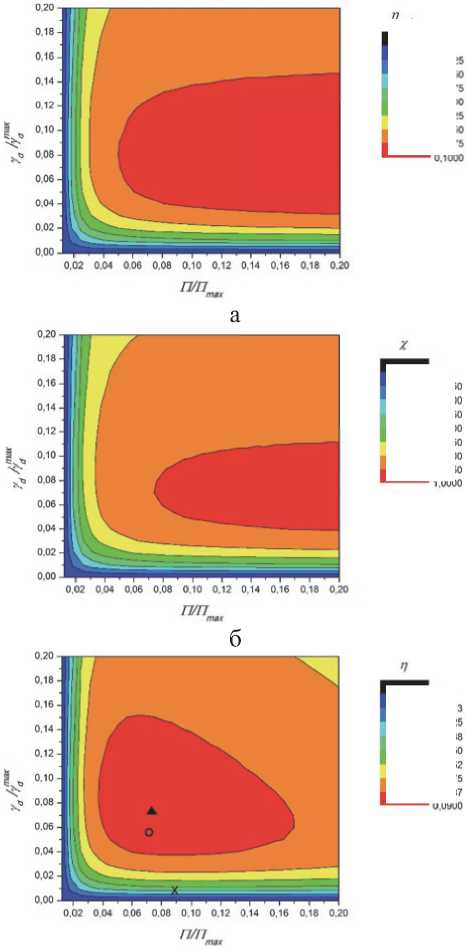
в

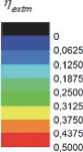
Рис. 2. Зависимости выходных характеристик непрерывного ЭКИЛ [3]: а – эффективности извлечения энергии из активной среды η _extm, б – параметра χ , в – энергетической эффективности η как функции критериев подобия γ _d и ∏ в нормированных координатах.

Обозначения символов на рис. 2, в: ▲ - наиболее эффективный расчетный режим генерации, × – экспериментальное значение, ○ – оценочное значение

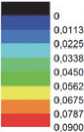
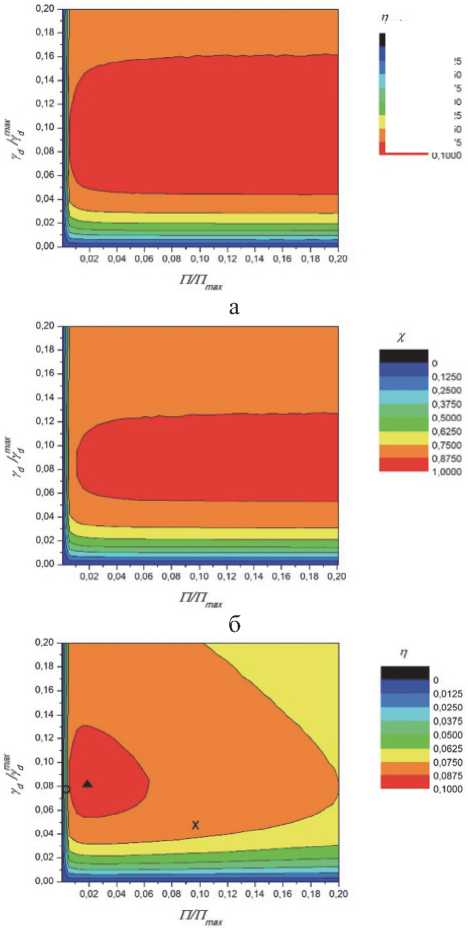
в

Рис. 3. Зависимости выходных характеристик непрерывного ОКИЛ [8]: а – эффективности извлечения энергии из активной среды η _extm, б – параметра χ , в – энергетической эффективности η как функции критериев подобия γ _d и ∏ в нормированных координатах.

Обозначения символов на рис. 3, в: ▲ - наиболее эффективный расчетный режим генерации, × – экспериментальное значение, ○ – оценочное значение

в [14] реализация высоких превышений ( ∏>8 ) на практике нецелесообразна, в случае лазера с оптической накачкой зависимость η от превышения является более крутой, чем для лазеров с химической накачкой и накачкой газовым разрядом.

Метод оценки максимальной энергетической эффективности, представленный в разделе «Математическая модель», дает величины η, мало отличающиеся от полученных по методу картирования. Близкими являются и значения критериев подобия γd и ∏, соответствующие максимальной энергетической эффективности (см. табл. 3). Однако вычисления в данном случае намного проще, и даже не требуют использования компьютера для прогнозирования оптимального режима. Следует отметить, что оценочные значения максимальной η во всех трех случаях расположены по оси γd /γdmax ниже полученных по методу картирования. Это свидетельствует о необходимости работать на восходящей ветви зависимости η=f(γd ) при конечной длине резонатора в направлении газового потока.

В таблице 4 даны сведения об экспериментально реализованных режимах генерации для непрерывных ХКИЛ [1] и ЭКИЛ [3] и для предполагаемого к созданию ОКИЛ [9].

Видно, что различие между энергетической эффективностью η _cal , вычисленной методом картирования, и фактической η _exp для ХКИЛ [1] не превышает 1 %. Несмотря на то, что ЭКИЛ [3] работает в режиме, лежащем за пределами красной области на графике (рис. 2), его эффективность также определяется этим методом с высокой точностью [16]. Сказанное свидетельствует о применимости метода картирования для анализа выходных характеристик непрерывных КИЛ в практически важных случаях, когда обеспечиваются малые потери. Метод оценки несколько завышает максимальную достижимую величину η , давая при этом достаточно близкие к оптимальным значения критериев подобия γ _d и ∏ .

Как указывалось в [13–15], достижение высоких значений η является результатом подбора режима работы лазера таким образом, чтобы значения критериев подобия γ _d и ∏ находились в определенных интервалах. Это необходимо для создания высокой инверсии при малых потерях энергии в релаксационных процессах и обеспечения оптимального коэффициента связи с внешней средой. При этом важно, чтобы молекулы энергоносителя O₂(¹∆) успели передать свое возбуждение атомам йода в реакции накачки (2). Можно проследить четкую взаимосвязь между значением γ _d и потерями «на вынос» из резонатора ∆ Y_out ⁄( Y_i – Y_TH ). Малая величина γ _d для ЭКИЛ [3] указывает на неоптимальную длину резонатора в направлении потока: энергия возбужденных частиц не успевает трансформироваться в излучение. Соответственно потери «на вынос» составляют около 60 %. Именно это является причиной, по которой максимальная расчетная энергетическая эффективность элек-троразрядного КИЛ более чем в 2 раза превышает достигнутую в эксперименте.

Красная область на графиках энергетических характеристик (рис. 1–3) в направлении оси γ _d/ γ _d ^max достаточно широкая во всех трех случаях (типично около 0,1). Однако поскольку расчетная

Таблица 2. Наиболее высокие выходные характеристики непрерывных КИЛ с различными типами накачки, прогнозируемые согласно методу картирования

Y d	Y d /Y d^	П	П/П тах	Л саЬ %	Работа
6,2	0,06	7,1	0,07	42,0	[1]
5,4	0,07	8,7	0,07	8,5	[3]
4,1	0,08	18,2	0,02	9,1	[9]

Таблица 3. Выходные характеристики непрерывных КИЛ с различными типами накачки, полученные с использованием метода оценки максимальной энергетической эффективности

Y d	Y d /Y max	П	П/П тах	^ саЛ , %	Работа
4,7	0,05	7,6	0,08	47,3	[1]
4,2	0,06	8,5	0,07	9,2	[3]
3,9	0,08	4,3	0,01	9,0	[9]

Таблица 4. Наиболее эффективные экспериментальные режимы работы непрерывных КИЛ

Y d	Y d /Y max	П	П/П тах	Л ехр , %	Работа
4,3	0,04	8,0	0,08	42,1	[1]
0,6	0,01	10,7	0,09	3,2	[3]
2,4	0,05	96,8	0,10	–	[9]

модель содержит не все [20], а только наиболее скоростные релаксационные процессы, фактически наклон поверхности в вертикальном направлении после прохождения максимума более крут. Таким образом, высокий темп кинетических потерь ограничивает зону эффективных режимов генерации частью красной области поверхности, восходящей к максимуму со стороны оси ∏/∏_max . Это означает, что для реализации режимов работы лазера с высокой энергетической эффективностью необходимо точно подобрать время пребывания активной среды в резонаторе. Согласно [14–16], оптимальные значения γ _d расположены в интервале от 4 до 6. Настоящая работа подтверждает этот вывод. В экспериментальных работах, выбранных для сравнительного анализа, потери энергии синглетного кислорода на релаксацию значительны (3 %) только в случае ХКИЛ (см. табл. 1 в [16]), где концентрации компонентов, тушащих возбужденное состояние атомов йода, высокие.

Для достижения высокой энергетической эффективности непрерывных КИЛ необходимо обеспечить оптимальный коэффициент связи с внешней средой при известных оптических потерях α [21]. Зависимость интенсивности излучения от коэффициента пропускания называют «кривой Ригрода». Согласно (9), энергетическая эффективность представляется в виде произведения эффективности извлечения энергии из активной среды и эффективности резонатора. Наличие максимума на кривой J(tr ) связано с тем, что с ростом превышения (или, что – то же самое с точностью до коэффициента порядка 0,5, с ростом отношения коэффициента усиле- ния слабого сигнала к пороговому) эффективность извлечения энергии из активной среды возрастает, а эффективность резонатора, наоборот, линейно спадает.

Как утверждалось в [14, 16], оптимальные превышения для непрерывных ХКИЛ и ЭКИЛ находятся в диапазоне от 3 до 8, так как рост отношения коэффициента усиления слабого сигнала к пороговому коэффициенту усиления при заданном значении α ( ∏_max ) не позволяет добиться увеличения энергетической эффективности. При ∏ >8 эффективность извлечения энергии из активной среды невозможно увеличить более, чем на 2–3 % [13], а эффективность резонатора, согласно (13), спадает достаточно быстро. Кроме того, реализация режимов с высокими превышениями на практике затруднена, поскольку с ростом интенсивности поля возрастают требования к лучевой стойкости оптики. Как показывают расчеты, выполненные для ОКИЛ, существенно расширить диапазон оптимальных значений ∏ и сдвинуть максимум энергетической эффективности в сторону более высоких превышений, можно только, увеличив ∏_max , либо за счет усилительных свойств среды, либо за счет потерь.

Представление результатов расчета выходных характеристик непрерывных КИЛ в виде цветовой карты позволяет сделать вывод, что эффективный режим генерации реализуется только для химического КИЛ [1]. В случае электроразрядного КИЛ [3] значение ∏ также попадает в диапазон эффективных режимов генерации, значение же γ _d достаточно далеко от оптимального. Для КИЛ с оптической накачкой

• [9 ] однозначные выводы до проведения экспериментов делать затруднительно, поскольку величина ∏_max представляется нереальной из-за невероятно высокой концентрации атомарного йода в газовом потоке. Пути повышения энергетической эффективности непрерывных КИЛ: снижение потерь синглетного кислорода на диссоциацию, уменьшение кинетических и оптических потерь, увеличение концентрации атомов йода и изменение длины резонатора в направлении потока рассмотрены в [16].

Сравнительный анализ расчетных и экспериментальных данных позволяет заключить, что для химического КИЛ максимальная энергетическая эффективность (~40 %) практически достигнута. Прогнозируемая наивысшая эффективность ЭКИЛ и ОКИЛ приблизительно одинакова. При этом на сегодняшний день она почти в 5 раз меньше, чем для химического лазера, даже, несмотря на то, что и электроразрядный и оптический КИЛ работают при сверхзвуковых скоростях потока (числа Маха >2), что позволяет снизить пороговую долю синглетного кислорода Y_TH до 1–3 %. Привлекательность электро-разрядного и оптического КИЛ определяется отработанностью технологий энерговклада в активную среду с помощью газового разряда и оптической накачки. Перспективы лазеров таких типов в значительной степени будут зависеть от характеристик генераторов синглетного кислорода, поскольку повышение доли O₂(¹∆) в газовом потоке представляется наиболее радикальным способом увеличения их энергетической эффективности [16, 22].

ЗАКЛЮЧЕНИЕ

На основе двухуровневой модели генерации, учитывающей наиболее значимые кинетические и оптические потери, модифицирован метод картирования режимов работы непрерывных КИЛ с различными типами накачки. Это позволило использовать для прогнозирования выходных характеристик двумерные графики, на которых энергетическая эффективность представлена в виде цветовой карты в нормированных координатах как функция двух критериев подобия: γd, выражающего безразмерное время, за которое доля синглетного кислорода доступная для извлечения в активной среде уменьшается в e раз при бесконечно большой интенсивности поля в резонаторе, и ∏, выражающего отношение максимального коэффициента усиления слабого сигнала при 100%-ной инверсии к пороговому, определяемому величиной потерь. Введение в расчетные уравнения дополнительных членов, описывающих кинетические (критерием Λ) и оптические (коэффициентом α) потери, дало возможность не только с высокой точностью предсказывать предельные энергетические характеристики непрерывных КИЛ, но и определять режим, при котором они достигаются.

Разработан метод упрощенной оценки максимальной энергетической эффективности непрерывных КИЛ, заключающийся в определении режима генерации на основе уравнений, полученных для случаев сильного поля и отсутствия кинетических потерь. В качестве исходных данных для расчетов здесь необходимы всего три параметра – начальная Y_i и пороговая Y_TH доли синглетного кислорода и критерий Λ , выражающий отношение скоростей релаксации и возбуждения для электронно-возбужденных атомов йода. Как правило, эти величины приближенно известны до проведения экспериментов.

Сравнительный анализ результатов расчетов выходных характеристик и имеющихся экспериментальных данных показал применимость обоих разработанных методов в практически важных случаях, когда обеспечиваются низкие кинетические и оптические потери. Также рассмотрены возможные пути повышения энергетической эффективности непрерывных КИЛ с различными типами накачки.