Прогнозирование эрозионного износа титановых сплавов в условиях длительного каплеударного воздействия

Введение. Исследованию эрозионного износа лопаток паровых турбин посвящено множество научных публикаций. Однако среди них очень непросто обнаружить исследования прогностического плана, которые моделировали бы поведение материала лопаток при длительных сроках эксплуатации [1—6]. Трудность построения расчётных оценочных моделей обусловлена рядом обстоятельств, главным из которых является большое число параметров, которые влияют на износ и которые необходимо учитывать при моделировании. Среди параметров, формирующих износ лопаточного аппарата, такие разнородные характеристики, как конструктивные особенности и режим работы турбины, наличие и устойчивость жидких плёнок на различных элементах проточной части турбин, включая поверхности лопаток, геометрия лопаток, кинетические параметры двухфазного потока, состав и дисперсность жидкой фазы потока и её распределение по поверхности лопатки, структура и свойства материала лопаток. Следует также добавить такие трудно поддающиеся учёту динамические явления, как вибрация, динамические напряжения в конструкции, постоянно меняющийся рельеф разрушающихся функциональных поверхностей. Дополнительная сложность заключена в том, что эмпирические данные об износе лопаток мощных паровых турбин не находятся в свободном доступе. Их можно получить только при плановых осмотрах и ремонтах турбин, промежутки между которыми составляют достаточно длительные сроки, рег ламентированные нормативными документами Минэнерго

Рис. 1. Общий вид кривой эрозионного износа и её основные параметры

При перечисленных сложностях основным источником опытных данных по каплеударной эрозии служат обычно стендовые испытания специальных образцов. Результатом таких испытаний является кривая эрозионного изнашивания, типичный вид которой приведён на рисунке 1.

Каплеударный эрозионный износ имеет три характерных периода: инкубационный, переходный и асимптотический. При относительно небольшом количестве ударов капель, которое возможно получить на стенде, каждый из них является практически линейным. Если для инкубационного и переходного периодов линейное приближение вполне корректно [7—9], то данные по длительной эксплуатации лопаток показывают, что кривая износа на асимптотической стадии далека от линейной. Каплеударный эрозионный износ формируется под действием локальных циклических ударных нагрузок, поэтому в значительной степени является усталостным процессом и описывается сложной степенной функцией [10—12]. В силу этого обстоятельства, а также из-за специфики проведения испытаний (фронтальный характер соударений, фиксированный размер капли, плоская поверхность образцов и т. д.) и ограниченного ресурса времени работы испытательного стенда, которое не превышает нескольких часов, по полученным кривым износа трудно делать прогнозы о долгосрочном износе лопаток.

Таким образом, цель настоящей работы может быть определена как построение модели для оценки эрозионного износа материала лопаток при длительной эксплуатации (десятков тыс. часов) на основе данных стендовых испытаний образцов из этих материалов. Причём из множества приведённых ранее параметров, формирующих износ, модель основывается на свойствах материала и параметрах соударений. Наиболее корректным её использованием представляется сравнительная оценка износа различных материалов по отношению к наиболее типичному материалу, эрозионный износ которого принимается за единицу.

Экспериментальная часть. Для испытаний использовали образцы особой грибовидной формы из титанового сплава ТС-5 (в двухфазном а+р-состоянии с твёрдостью 2565 МПа). Каплеударная эрозия моделировалась на уникальном эрозионном стенде НИУ-МЭИ «Эрозия-М» [7] в виде воздействия на образец монодисперсного водно-капельного потока, схема которого показана на рис. 2. Параметрами соударения капель с мишенью (поверхностью образца) являются диаметр dk (или радиус R) капли и скорость образца V_o.

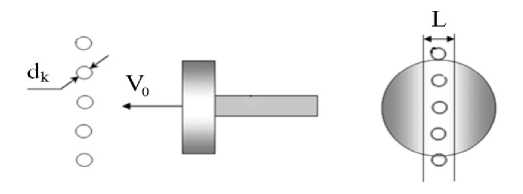
Рис. 2. Схема взаимодействия образцов с каплями жидкости: L — ширина эрозионного следа-дорожки

Результаты проведённых испытаний представлены на рисунке 3 в виде кривых эрозионного изнашивания. Величины, расположенные по осям абсцисс на графиках, характеризуют интенсивность воздействия капель эродента (воды), выраженную в различных взаимопереводимых единицах. Аналогичным образом по осям ординат расположена по-разному выраженная интенсивность износа образцов. Важным результатом экспериментов является то, что переходный и асимптотический периоды эрозионного износа характеризуются каждый своим семейством линий, начинающихся в собственном «полюсе» — 5) для переходного и Ei для асимптотического периодов, а скорость изнашивания, характеризуемая наклоном соответствующей линии к оси абсцисс, определяется параметрами соударения 1/₀ и dk. При этом положение каждого из «полюсов» Еь и Ei определяется структурой и свойствами материала [13,14].

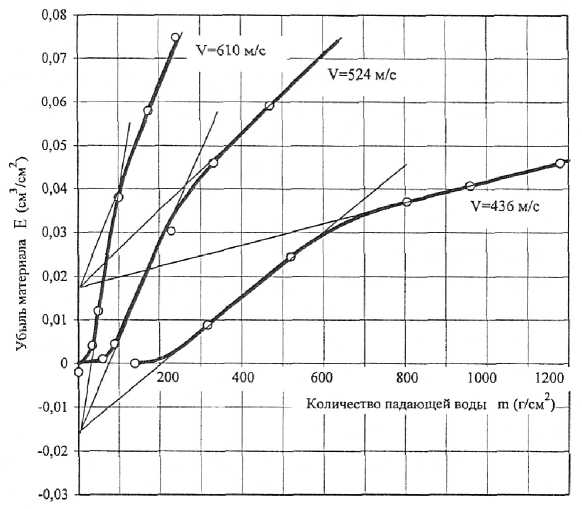
Рис. 3. Зависимости каплеударного эрозионного износа образцов титанового сплава ТС-5 по данным стендовых испытаний при dt = 270 мкм и l/= Vo

Аналитическая часть. В общем виде закон ударно-усталостного изнашивания обычно выража ется в дифференциальной форме [10]:

dW= (dW/dN) ■ dN + (dW/da) ■ do (1) где W— объёмный износ (в дальнейшем экспериментальные значения объёмного износа обозначаются буквой Е, а расчётные — буквой W); о — нормальное напряжение; /V —число циклов.

Если износ не зависит от геометрии контакта, то правая часть уравнения (1) становится малой. Линейная зависимость W от /V имеет место, например, при ударно-абразивном изнашивании [11]. В более общем случае эта зависимость нелинейна [10,12]:

W = k-Nⁿ-G^m (2)

где к, п, т— коэффициенты.

Нормальное напряжение о (как и максимальное контактное давление) определяется максимальной силой удара Р_т, которая в свою очередь зависит от скорости соударения 1/₀, геометрии контакта и свойств материала.

Максимальная контактная нагрузка Р_т в зоне соударения определяется по Эвансу [15] из выражения, фактически эквивалентного кинетической энергии капли:

Р_т=0_г5.к^.Р^г.р                            (3)

Для вычисления давления, развиваемого силой Р_т на поверхности материала в пределах площади контакта капли, отнесём Р_т к площади среднего сечения капли S = и-Р⁷. Получим соответствующее напряжение на поверхности материала Q_m в момент соударения:

Q_m = 0,5-V_o²-P                                           (4)

Ранее уже говорилось, что полностью описать какую-либо кривую эрозии (из представленных на рисунках 1 или 3) с помощью одной математической функции невозможно, поэтому каждую стадию эрозии необходимо рассматривать по отдельности и для каждой определить свою функцию.

1. Для инкубационной стадии примем следующую усталостную модель: под действием давления, развиваемого каждой каплей Qm, происходит микропластическая деформация или даже (возмож- но) образуется радиальная субмикротрещина длиной !к; она имеет размер, не превышающий линию Френча на кривой усталости данного материала; каждый удар капли по гипотезе Пальмгре-на — Майнера накапливает деформацию, напряжения и увеличивает трещину; в какой-то момент это приводит к зарождению боковой трещины 4; к моменту начала эрозионного износа Т1п (окончание инкубационной стадии; см. рисунок 1) должна сформироваться боковая трещина критического размера 4 = 4> вызывающая разрушение в виде дискообразного фрагмента — первой частицы износа объёмом И (для хрупких материалов типа стекла эта частица может иметь форму конуса Герца); количество циклов нагружения (ударов капли) к этому моменту известно — это количество эродента Tin на графике, [кг/м2], соответствующее началу процесса потери массы при соответствующем значении 1/0. Чтобы выразить Т1п в числе циклов усталостного нагружения Ne (то есть в числе капель, попавших в одну точку к моменту Т^ и тем самым окончательно перейти на язык моделей усталости и циклического нагружения, воспользуемся выражением:

Ne:=

3-7;

4 - р-/?

Экспериментальные (из рисунка 3) и расчётные (по выражениям, приводимым далее в тексте) значения характерных точек всех кривых изнашивания сплава ТС-5, сведены в таблицу 1 (см. далее).

Известно, что любая кривая усталости в логарифмических координатах 1g ст — 1g /V представляет собой наклонную прямую (линейная функция), в том числе и линия начала эрозионного износа T_in. В логарифмических координатах для определения такой функции достаточно знать координаты двух точек, через которые она проходит. С другой стороны, в линейных координатах ст — /Vфункция является степенной (см. выражение (2)). То есть, зная координаты двух точек каждой кривой износа, можно определить показатель наклона т_е линии начала эрозионного износа Тп на графике усталости (т. е. при износе Е= 0 см³/см² для различных значений 1/₀ на рисунке 3).

Так, показатель наклона т_е линии начала эрозионного износа T_in на диаграмме усталости можно рассчитать по выражению (6), где (ст_е, /V_e) — координаты точки на кривой усталости (для определения т_е необходимо знать координаты, как минимум, двух таких точек, рисунок 3 даёт нам три таких точки — для каждого значения 1/₀, а в качестве ст_е принимается значение Q_m для соответствующего 1/₀):

те := — ig

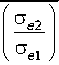
Вычисления дают следующее значение показателя наклона линии начала эрозионного износа Т_1п на диаграмме усталости титанового сплава ТС-5: гп_е = 2,75. Тогда сама линия напряжений начала износа а_ер в зависимости от количества циклов нагружения N_e будет задана выражением:

стеДА/е):=10п(Ч где

' v те где N6r = 3,3 • 105 — предельное число циклов малоциклового нагружения, в пределах которого применима данная расчётная модель для инкубационной стадии; оеК — значение предела капельно-ударной усталости, [МПа], оно соответствует минимальному значению внешнего на- пряжения, необходимого для начала пластической деформации (для начала скольжения дислокаций под действием касательного напряжения т* в плоскости скольжения); для титана значение стеЛ составляет 28 МПа [16].

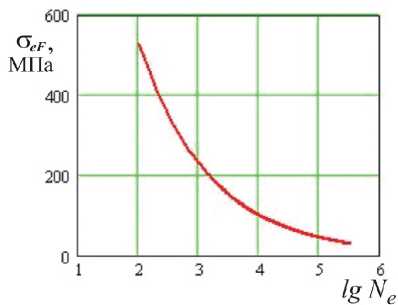
Рис. 4. Зависимость напряжений с_ер начала эрозионного износа сплава ТС-5 в зависимости от количества циклов нагружения N_e (ударов капель)

Расчётный график линии старта эрозионного износа о_ер показан на рисунке 4. График характерен тем, что при значении /V = 1 (в точке пересечения графика с осью напряжений) даёт значение напряжения а_ер = 2826 МПа, что соответствует уровню твёрдости сплава ТС-5 (измеренная твёрдость составляла Н = 2565 МПа). На обычных кривых усталости (получаемых при испытаниях по методикам ГОСТ) эта точка соответствует обычно пределу прочности о_в. Для эрозионного же износа получается значение почти в 3 раза выше о_в, что вполне отвечает теоретическим положениям о поверхностном характере явлений эрозионного изнашивания и необходимости преодоления барьера напряжений уровня твёрдости материала для начала эрозионного износа.

Для определения начальной точки эрозионного износа, лежащей на горизонтальной оси Е = 0 на рисунке 3, можно воспользоваться выражением (8), в соответствии с которым рассчитывается, сколько понадобится эродента, [кг/м²], для того, чтобы стартовал процесс износа:

Tin(R,voy.= yP-R-NeR.

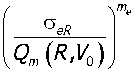
где все значения уже определялись ранее, a T_in и Q_m выражены как функции от параметров соударения R и Vq.

То же самое можно определить в циклах нагружения (в количестве ударов капель, попавших в одну точку к моменту начала износа):

Nin^,Voy.= NeR.

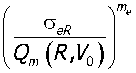
Как показывают расчётные данные, приведённые в таблице 1, выражение (8) обеспечивает высокую степень соответствия результатов расчёта с экспериментальными данными рисунка 3. 2. Для асимптотической стадии в соответствии с моделью малоцикловой усталости выполнены аналогичные (как и для инкубационной стадии) расчёты по определению показателя наклона кривых усталости.

Следует отметить, что, как свидетельствуют данные таблицы 1, кривые эрозионного износа, представленные на рисунке 3, практически полностью лежат в области малоциклового нагружения. Это объясняется тем, что они получены в лабораторных условиях на испытательном стенде. Рабочие же лопатки паровых турбин должны служить не один год, поэтому асимптотическая стадия таких изделий должна рассчитываться по моделям многоцикловой усталости. Принципиальная разница состоит в том, что кривые износа в малоцикловой области близки к линейной функции (или к степенной, но с показателем степени, близким к единице), как это и следует из рисунка 3, а износ при многоцикловой усталости описывается степенной функцией с показателем, далёким от единицы (из-за чего, собственно, эта стадия и называется асимптотической).

Таблица 1

Числовые значения экспериментальных и расчётных параметров кривых эрозионно-капельного износа сплава ТС-5 (рис. 3, радиус капель R = 135 мкм)

Скорость соударениям о, м/с	610	524	436
Напряжение удара Qm = се, МПа	186	137	95
Окончание инкубационной стадии: расход эродента Т,п = гп;п, г/см2 (при Е = 0 см3/см2)	32	75	203
То же в количестве соударений Nn при Е = 0 см3/см2, циклов	1778	4166	11278
Начало асимптотической стадии: расход эродента Tas = m».s, г/см2	100	265	637
То же в числе соударений Nas, циклов	5556	14722	35388
То же в потерях металла Eas, см3/см2	0,04	0,013	0,03267
Переходная стадия: расход эродента од,ог при Е = 0,02 см3/см2, г/см2	62,5	162	458
То же в числе соударений ЛЬ.ог, циклов	3472	9000	25440
Асимптотическая стадия: расход эродента од,04 при Е = и,ич СМ /СМ , Г/СМ	100	252	923
То же в числе соударений ЛЬ,о4, циклов	5556	14000	51280
Асимптотическая стадия: расход эродента од,044 при Е = 0,044 см3/см2, г/см2	121	330	1177
То же в числе соударений ЛЬ,044, циклов	6722	18330	65390

Поэтому здесь мы рассматриваем асимптотическую стадию эрозионного изнашивания в соответствии лабораторными данными рисунка 3 на основе малоцикловой модели. Далее же, рассматривая эрозию рабочих лопаток, воспользуемся многоцикловой моделью (см. п. 4).

Итак, на базе малоцикловой модели по аналогии с методикой расчёта инкубационной стадии, рассмотренной выше, выполнены расчёты для трёх точек кривых эрозионного износа (по одной на каждой кривой рисунка 3), соответствующих значению износа материала Е = = 0,04 см³/см², и трёх точек при Е = 0,044 см³/см² (см. таблицу 1). Получено значение показателя наклона линии асимптотической стадии эрозионного износа в малоцикловой области на диаграмме усталости титанового сплава ТС-5: гп_е = 3,38.

• 3.    Для эрозионной кривой на переходной стадии используем линейную аппроксимацию, что для достаточно короткого участка, находящегося в малоцикловой области, вполне допустимо. В расчётной модели ставилась задача нахождения расчётным путём точки начала асимптотической стадии (значения Tas, Nas, m_AS, E_AS в таблице 1 и на рисунке 3). Поскольку эта точка для любой скорости соударений лежит в области малоцикловой усталости, она вычислялась как точка пересечения линейных аппроксимационных функций переходной и асимптотической стадий. Эти функции даны на рисунке 1, там они пересекаются в точке с координатами (t_n, МД. В качестве расчётных выражений использованы:

• -    функция износа на переходной стадии в зависимости от числа соударений /V_e:

WAN^idwN--E«                 (10)

• -    то же на асимптотической стадии вблизи точки (tn, МД\

W^N.> ^E_.k                       (И)

'in ^ / ^0 ) Kdr где kdr = tg у / tg а — коэффициент дробления капель (углы у и а см. на рисунке 1); величина Nin входит в выражения (10) и (11) как функция от параметров соударения (R, 1/0); функция W эквивалентна Ена рисунке 3; индекс Lу функции ^означает линейную аппроксимацию.

Пример расчёта для значений R = 135 мкм; 1/₀ = 436 м/с; Е> = 160 мкм; 5 = 177 мкм; k_dr = = 3,07 представлен на рисунке 5. График показывает, что слева от точки пересечения эрозия развивается по линии переходной стадии 1, а справа — по линии асимптотической стадии 2.

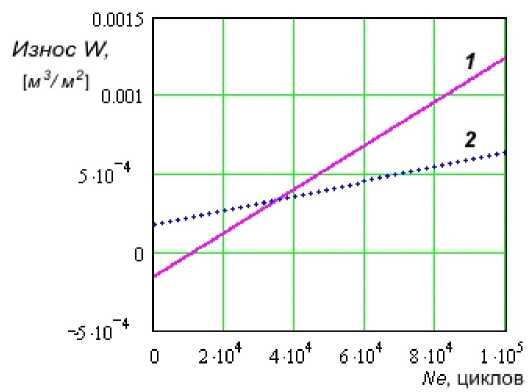
Рис. 5. Зависимость износа И/, [м³/м²], сплава ТС-5 при скорости соударений V& = 436 м/с на переходной 1 и на асимптотической 2 стадиях эрозии от количества циклов нагружения N_e (ударов капель)

Точка начала асимптотической стадии при линейной аппроксимации эрозионной кривой представляет собой точку пересечения двух прямых переходной и асимптотической стадий на рисунке 5. Условием для нахождения этой точки является равенство W_p ^N^ = W_ASl (/V_e), из которого находятся:

• -    абсцисса точки в циклах нагружения (в ударах капель):

N_as (R,V_oy.= N_in(R,V^ --f

• -    абсцисса точки в единицах массы эродента, [кг/м²]:

• 4.    Для асимптотической стадии основная задача работы была сформулирована как нахождение математической функции для описания величины эрозионного износа в соответствии с моделью многоникловой усталости . Сложность задачи состояла в том, чтобы единая функция максимально точно описывала как малоцикловой этап асимптотической стадии в районе точки (t_n, МД рисунка 1, так и многоцикловой этап в приближении к эксплуатационному пределу лопатки.

TAS(R,Voy.= Tin(R,V^--^

Ордината точки находится простой подстановкой значения N_AS, полученного из выражения (12), в выражение (11) в качестве N» Так, для исходных данных, при которых получен график (5), точка начала асимптотической стадии имеет следующие расчётные координаты: M_AS = 35610 циклов; T_AS = m_AS = 6410 кг/м² = 641 г/см²; W_ASL = V_AS= 3,4 • 10^-4 м³/м² = 0,034 см³/см². Сравнение с данными таблицы 1 даёт высокую степень совпадений расчётных и экспериментальных значений.

Физическая сущность рассматриваемой точки начала асимптотической стадии состоит в формировании эрозионно-стойкого рельефа, приводящего к дроблению капель и замедлению скорости эрозии [13].

Линейная аппроксимация асимптотической стадии эрозии, которой мы воспользовались ранее (см. п. 2), возможна только на самом раннем этапе этой стадии, когда эрозия находится в малоцикловой области, например, в окрестности точки (t_n, МД рисунка 1. Это допущение мы и использовали при вычислении координат точки начала асимптотической стадии (t_n, МД. Для прогнозирования многоцикловой эрозии рабочих лопаток линейная аппроксимация невозможна. В этом можно легко убедиться, просчитав потерю массы (или объёма) лопатки по выражению (11). Даже для минимального ресурса работы лопатки 50000 часов, предусмотренного ГОСТом (при рассматриваемых скоростях соударения 1/₀ = 250...613 м/с это составляет около 5,7 лет непрерывной работы), эрозионный износ, вычисленный по линейному закону, превышает толщину лопатки в несколько раз.

В результате исследований для прогнозирования износа титановых сплавов в модели многоциклового нагружения предложена следующая аппроксимационная функция для величины эрозионного износа Was в зависимости от количества соударений N_e (числа циклов нагружения):

. /у ^meAS

__!F

.IMmeAS

^eR 'eR где все величины встречались ранее в тексте, пояснения требуют лишь meAs и NeR, первая из них meAs = 3,38 — показатель наклона линии асимптотической стадии эрозионного износа в малоцикловой области на диаграмме усталости сплава ТС-5, был определён ранее (см. п. 2); N6r = (2...3) • 1010 — предельное число циклов («база») многоциклового нагружения, в пределах которого применима данная расчётная модель для асимптотической стадии; в данном случае за «базу» принимается срок эксплуатации лопаток в 50000 часов непрерывной работы; величина N6r встречалась в формуле (7), но там она представляла собой «базу» малоцикловой усталости.

Аппроксимационная функция W_AS по выражению (14) определяет объём эродированного материала, [м³/м²], в зависимости от количества ударов капель N_e в предположении, что удаление материала происходит под циклическим действием напряжения Q_m, а глубина эрозионной повреждаемости определяется свойствами материала (5)) и сформированным рельефом (ЕД, который определяет степень дробления капель на асимптотической стадии (k_dr\ Функция W_AS начинается в точке Е (в области отрицательных значений Е), проходит максимально близко к точке начала асимптотической стадии (точка (t_n, МД на рисунке 1) и даёт устойчивую корреляцию с линейной функцией W_ASl в области малоциклового нагружения (т. е. в начале асимптотической стадии). Прогностическая функция W_AS не обеспечивает совпадения с кривой эрозионного изнашивания на начальных (инкубационной и переходной) стадиях, но хорошо коррелирует с эмпирическими данными износа лопаток при длительной эксплуатации.

В качестве расчётного примера на рисунке 6 представлена аппроксимационная функция Was сплава ТС-5, полученная для тех же исходных данных, что и функции W_Pn W_Asl на рисунке 5.

В хорошем соответствии расчётных и экспериментальных результатов можно убедиться из сравнения данных рисунка 6 би таблицы 1.

В заключение приведём результаты (см. рисунок 7) аппроксимации величины эрозионного износа сплава ТС-5 в районе точки начала асимптотической стадии (точка (tn, МД на рисунке 1), выполненные с помощью различных функций. Из сравнения графиков на рисунке 7 ясно, что для оценки величины эрозионного износа рабочих лопаток паровых турбин в пределах срока эксплуатации линейная аппроксимация не годится из-за непомерно высоких значений износа, получаемых при большом числе циклов нагружения. Линейные функции могут быть использованы только в области малоциклового нагружения (главным образом, для переходной стадии), степенная же аппроксимационная функция И^5 может быть рекомендована для прогнозирования эрозионного износа в многоцикловой области вплоть до ресурса лопаток 70...100 тыс. часов эксплуатации.

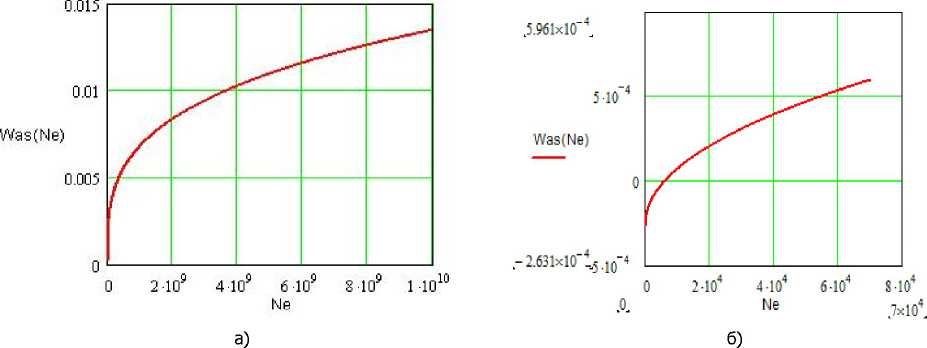
Рис. 6. Зависимость износа Was, [м³/м²], от количества циклов нагружения N_e (ударов капель) на асимптотической стадии каплеударной эрозии сплава ТС-5 при скорости соударений V& = 436 м/с: а — в интервале многоцикловой усталости; б — в пределах зоны малоцикловой усталости

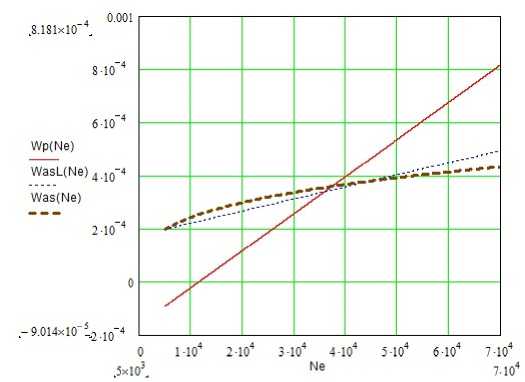
Рис. 7. Аппроксимация величины износа W, [м³/м²], сплава ТС-5 при скорости соударений V& = 436 м/с в условиях каплеударной эрозии с помощью различных функций: линейных Wp и И4я —для переходной и асимптотической стадий соответственно, а также сложной степенной функции Was — для асимптотической стадии

Заключение. Поставленная в работе цель реализована в виде аппроксимационной функции WAS, позволяющей на основе усталостной модели с достаточной степенью точности определять износ материала турбинных лопаток при длительных сроках эксплуатации, опираясь на данные кратковременных стендовых испытаний. Задача решена в программной оболочке MathCAD, предназначенной главным образом для исследовательских целей. Для решения прикладных задач на базе выполненных исследований целесообразно методики стендовых эрозионных испытаний дополнить специализированной компьютерной программой по прогнозированию величины эрозионного износа рабочих лопаток турбин при длительных сроках эксплуатации. В этом направлении в настоящее время авторы и продолжают свою работу.

Представленные результаты получены в рамках выполнения научно-исследовательских работ по Государственному контракту № 02.740.11.0813.