Прогнозирование неравенства в Казахстане по денежным доходам населения

В современном обществе перед каждым государством стоит задача обеспечения социальной справедливости и защищенности населения, а также сглаживание социального неравенства. Успехи социально-экономической политики выражаются, прежде всего, в более равномерном росте благосостояния всех граждан страны и сокращении избыточного неравенства между членами его общества.

Усредненные показатели доходов населения, такие как среднедушевой доход, среднедушевое потребление, не всегда отражают реальное экономическое состояние большинства домашних хозяйств в стране, и обязательно должны сопровождаться показателями, характеризующими их распределение и концентрацию. В связи с чем, показатели неравенства являются неотъемлемой частью оценки уровня жизни населения.

В официальной статистике Казахстана применяются следующие индикаторы неравенства: индекс Джини, коэффициент фондов, среднедушевое потребление по доходным группам населения (квинтильным, децильным), денежные расходы населения по доходным группам, распределение потребления по доходным группам, а также графическое изображение распределения населения по доходам через кривую Лоренса. Все эти показатели отражают, прежде всего, экономическое неравенство. В Казахстане они рассчитываются на основании дохода, использованного на потребление, а не денежных доходов населения .

В период 2001–2009 гг. в Казахстане основные показатели неравенства по потреблению (индекс Джини и коэффициент фондов) заметно снизились, однако в 2010–2011 гг. несколько возросли. Так, индекс Джини по децильным группам в 2011 г. согласно официальной статистике составлял 0,289, а коэффициент фондов, рассчитываемый как соотношение среднедушевых доходов 10% наиболее и 10% наименее обеспеченного населения – 6,1. В 2012 г. вновь наметилась тенденция к их снижению: индекс Джини составил 0,284, коэффициент фондов – 5,9.Ряд авторов, изучающих вопросы уровня жизни и неравенства в Казахстане, склоняются к тому, что рассчитываемые официальной статистикой показатели неравенства не всегда в полной мере отражают существующее положение [1-3].

Так, Агентство Республики Казахстан по статистике осуществляет расчеты основных индикаторов неравенства только по потреблению. При этом применяется агрегированный индикатор – доход, использованный на потребление ⁴.

Это очень хороший и информативный индикатор для расчета показателей бедности. Однако показатели сложившегося в обществе неравенства целесообразнее рассчитывать по денежным до-ходам ⁵, поскольку неравенство по денежным доходам населения может быть существенно выше и более точно отражает ситуацию с расслоением в казахстанском обществе. Кроме того, применение в эконометрической модели макроэкономических показателей денежных доходов, включающих дооценку теневых заработков и доходы всего населения, позволяет учесть при расчетах показателей неравенства все группы населения, включая как самых богатых, так и самых бедных.

В связи с этим, исследователями были поставлены две основные задачи:

• (1)    оценить степень неравенства в казахстанском обществе по показателям денежных доходов населения;

• (2)    на основе экономико-математического моделирования спрогнозировать показатели неравенства и распределения населения по денежным доходам на 2013–2014 гг.

Методология. В статистических исследованиях широко используется логнормальное распределение как математическая модель, достаточно точно отражающая распределение доходов в обществе. В основу методологии настоящего исследования были положены разработки российского ученого И.Б. Колмакова [4]. Применительно к распределению населения по среднедушевому денежному доходу x выяснено, что следующее выражение

р(х) =

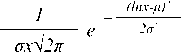
достаточно хорошо апроксимирует плотность этого распределения, где μ – математическое ожидание, σ – среднеквадратическое отклонение натурального логарифма случайной величины x. Эти два параметра определяют искомое распределение, и их можно оценить на основе выборочных характеристик по данным статистических обследований.

Математически нетрудно выявить связи между параметрами распределения (1) логарифма случайной величины х и параметрами распределения случайной переменной х :

lnx_c - ц + у- а², (2)

1пх_т д о, (3)

^Хе ^' (4)

где x_c – математическое ожидание, x_m – мода, x_me – медиана распределения случайной величины x. Заменяя эти характеристики распределения случайной величины x на соответствующие им выборочные аналоги номинальное среднее x_c , выборочное модальное значение x_m или выборочная медиана x_me среднедушевого месячного денежного дохода, можно получить формулы для оценки параметров логнормального распределения (1).

В работе российского ученого И.Б. Колмакова [4] параметры μσ оцениваются на основе соотношений (2) и (3), т.е. используются полученные путем проводимых обследований населения выбороч- ное среднее xc и выборочное модальное значение xm. Соответственно получаются формулы для параметров логнормального распределения:

p-^ln(X2XJ,

а²-^ ЦпХ₍ -InXJ,        (6)

А если использовать выборочное среднее xc и выборочную медиану xme среднедушевого денежного дохода, то в соответствии с (2) и (4) формулы для оценки математического ожидания и дисперсии логнормального распределения (1) примут вид ц InX^^f (7)

ст 2 ЦпХ_с 1пХ_те), (8)

Для оценки параметров можно также выбрать пару выборочного модального значения xm или выборочной медианы xme среднедушевого денежного дохода:

р IriX^,              (9)

а2 = 1пХ -1пХ ,

Оцененный закон распределения среднедушевого денежного дохода (1) служит основой для построения кривой Лоренца, которая, в свою очередь, позволяет вычислить показатели дифференциации населения по доходам, в частности, коэффициент Джини.

Для построения кривой Лоренца следует сначала определить точки x₀ , x₁ , ... , x_n такие, что в каждый интервал ( x_j-1 , x_j ), j=1,2, ..., n, попадает доля, равная 1/n всего населения, упорядоченного по возрастанию среднедушевого месячного денежного дохода x . При этом x₀ =0. Остальные значения x_j определяются из условия

• 1           (1™- м)²         /

  --I —е 2я² Дх = —,    / = 1,2,...,п.

ау2тг1 х                п "

О true— р

Замена z ~ а

переменной интегрирова-

ния приводит к условию для вычисления величины z :

j

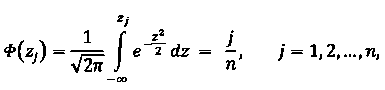
где Ф (z)– функция Лапласа, которая является затабулированной функцией. Учитывая замену переменной интегрирования, находим искомые значения

• х, = e^oz)⁺^, j = 1,2,..., И- (11)

Теперь можно вычислить ординаты y ₁, ... , y_n точек кривой Лоренца, соответствующие значениям 1/ n , 2/ n , ... , n / n ее абсциссы. Причем y ₀=0 и y _n=1. Кумулятивный денежный доход населения с денежными доходами в интервале от 0 до x_j равен:

xj

1 г (tnx- ^)² К = —I e~ 2a² dx ^J (TN^nJ

о

Выберем следующую замену переменной инте-Inx- u- a2 „          , грирования: W =          . После преобразо ваний получим:

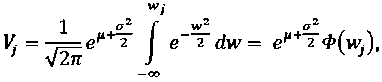
InKj— [i— a2

где j a . Если верхний предел интегрирования устремить к ∞, то согласно свойству функции Лапласа отсюда следует, что суммарный

( cr2

денежный доход населения равен e^+ 2 Разделив на эту величину, найдем долю кумулятивного денежного дохода населения в интервале от 0 до

x : j

Vj = Ф^^-^-сг), ; = l,2,...,n.

Чем больше число интервалов n , тем точнее будет аппроксимироваться кривая Лоренца. На практике обычно строят квинтильную (при n =5) или децильную (при n =10) кривую Лоренца.

Как известно, для измерения уровня неравенства широкое распространение получил коэффициент Джини. Он представляет собой удвоенную площадь фигуры, заключенной в единичном квадрате между биссектрисой координатного угла и кривой Лоренца. Чем меньше величина коэффициента Джини, тем ниже уровень неравенства.

Таким образом, на основе параметров логнор- мального распределения можно построить кривую Лоренца и оценить уровень дифференциации населения по денежным доходам. Однако интерес представляет прогнозирование индикаторов, отражающих дифференциацию доходов. И это может быть осуществлено путем оценки ожидаемых значений характеристик распределения населения по денежным доходам. Для оценки прогнозных вели- чин математического ожидания μt+1 и дисперсии σ2t+1 в следующем году t+1 необходимы прогнозные значения выборочного среднего xct+1, выборочного модального значения xmt+1 или выборочной медианы xmet+1 среднедушевого среднемесячного денежного дохода. Тогда требуемые прогнозные величины μt+1 и σ2t+1 можно оценить по формулам (5)-(6), (7)-(8) или (9)-(10).

Информационная база. Для получения прогнозных значений параметров логнормального распределения среднедушевого денежного дохода использовались официальные данные за 2009–2012 гг., публикуемые Агентством РК по статистике [6-9]. Величину номинального среднедушевого среднемесячного денежного дохода x _{ct +1} можно представить как часть валового внутреннего дохода страны, которая используется в качестве денежного дохода населения, поделенную на численность населения и на число месяцев в году. Особо подчеркнем, что это макроэкономический показатель, т.е. рассчитанный для генеральной совокупности. Агентство по статистике РК не публикует прогнозы этого показателя. Поэтому остается предположить, что существует достаточно тесная связь между макро показателем номинального среднедушевого денежного дохода x _c и другими макроэкономическими показателями, и оценить ее, используя эконометрические методы для 2013–2014гг.

Для вычисления прогнозного модального значения денежного дохода xmt+1 выведена формула у _ у -^Ct+1 b ^tvi mt+1 mt x^ St+1 ds^ (13)

в которой величина DS_t представляет собой суммарный доход долей оплаты труда и трансфертов в структуре баланса доходов и расходов населения, а коэффициент k_{st +1} отражает компенсационное воздействие показателей структуры доходов на формирование показателя темпа роста модального значения дохода, и мало отличается от единицы [4].

В таблице 1 приведены фактические и расчетные (прогнозные) данные для Казахстана, используемые для построения кривой Лоренца и расчета коэффициента концентрации денежных доходов населения – индекса Джини. Значение среднедушевого месячного денежного дохода и доли суммарного дохода оплаты труда и трансфертов в структуре баланса доходов и расходов населения публикуются в сборниках «Уровень жизни населения Казахстана» АРКС. Прогнозные

Таблица 1.

Показатели доходов, используемые для прогнозирования неравенства за 2009–2012 гг. и прогнозируемые данные на 2013-2014 гг.

Показатель	2009	2010	2011	2012	2013	2014
Номинальный денежный доход на душу населения, в месяц, тенге1	34282	38779	45936	51755	59674	68803
Модальное значение денежного дохода на душу населения, в месяц, тенге2	12180	13810	15924	18282	20907	24077
Суммарная доля доходов оплаты труда и трансфертов в структуре баланса доходов и расходов населения3, %	86,4	86,6	84,3	85,9	85,2	85,1