Прогнозирование образования конкурирующих фаз при росте тонких пленок Cr2GaC на MgO(111)

В настоящий момент одним из наиболее перспективных направлений исследований, касающихся синтеза новых материалов, является изучение процессов формирования и физических свойств МАХ-фаз, семейство которых представлено на рис. 1. МАХ-фазы обладают малой плотностью, высокими значениями тепло- и электропроводности, прочности, пониженным модулем упругости, превосходной коррозионной стойкостью в агрессивных жидких средах [5–7], стойкостью к высокотемпературному окислению и термическим ударам [8–10], а также легко подвергаются механической обработке [11; 12], имеют высокую температуру плавления [13] и являются достаточно стабильными при температурах до 1000 °С и выше [14].

Хорошо известно, что тонкие плёнки MAX-фаз в основном синтезируются физическими методами, такими как магнетронное распыление импульсного осаждения слоёв. Проведение комплексного исследования магнитных свойств требует высокого качества магнитных тонких плёнок MAX-фаз. Плёнки самого высокого качества определяются как однофазные, монокристаллические и гладкие.

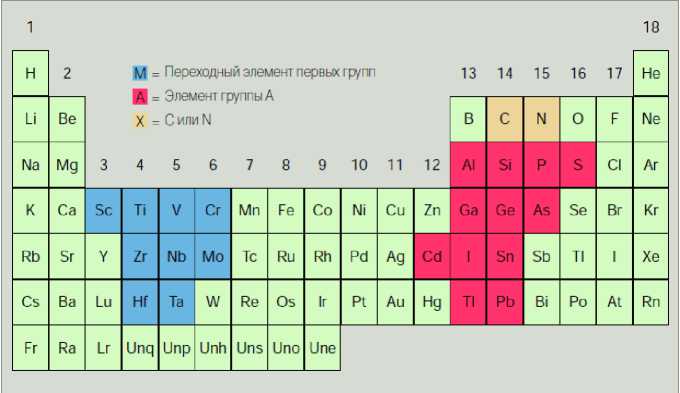
Рис. 1. Периодическая таблица элементов, образующих наноламинаты общего состава [2]

• Fig. 1.    The periodic table of the elements constituting the nanolaminates of general composition [2]

На качество получаемых плёнок влияют такие факторы, как температура осаждения, давление, мощность, подаваемая на магнетроны, т. е. исходящий/ входящий поток материала, а также выбор подложки. Для синтеза MAX-фаз необходимо рассмотреть конкурирующие бинарные или тройные фазы, близкие по составу и/ или структуре.

Рост эпитаксиальной плёнки Cr 2 GaC сопровождается ростом фазы Cr 3 Ga, которая не прогнозируется как конкурентная по стехиометрическому химическому составу [15]. Подложка, в свою очередь, может кардинально изменить ситуацию, как это наблюдается в случае Mn 2 GaC. При тех же условиях роста на любой другой подложке, кроме MgO, не было видимого сигнала MAX-фазы [15].

Таким образом, наша задача состоит в том, чтобы рассмотреть влияние изменения стехиометрии потока атомов на термодинамическую выгодность фазообразования, а также учесть роль границ раздела между подложкой и MAX-фазой и конкурирующими фазами.

Результаты и обсуждения

В этой работе мы изучаем MAX-фазу Cr 2 GaC. Для изучения этого соединения необходимо рассмотреть систему Cr-Ga-C. Задача состоит в том, чтобы рассмотреть все возможные реакции между чистыми элементами, доступными в различных количествах. Ниже приведён пример реакции.

2xCr + xGa + xC → Cr₂GaC + [competing] + α Cr + β Ga + θ C. (1)

В этом примере чистые элементы доступны в количествах, соответствующих стехиометрии MAX-фазы, т. е. Cr:Ga:C=2:1:1. в правой части уравнения коэффициенты при остатках чистых элементов обозначены греческими буквами. Конкурирующей фазой может быть любая из семи возможных фаз в системе Cr-Ga-C: CrGa 4 , Cr 5 Ga 6 , CrGa, Cr 3 Ga, Cr 3 C 2 , Cr 7 C 3 , Cr 23 C 6 .

Энтальпия одной конкретной реакции вычислялась не только в случае наличия элементов в количествах, соответствующих стехиометрии MAX-фазы, т. е. Cr:Ga:C=2:1:1, но и для всех возможных соотношений.

В силу большого объёма требовавшихся вычислений, было принято решение о написании специального кода в программном пакете “Matlab”. Внешними циклами стали циклы для i, j, k, под которыми понимаются атомарные доли хрома, галлия и углерода соответственно. При установлении границ цикла было учтено, что их сумма есть 1. Именно эти циклы отвечают за вычисление энтальпии каждой конкретной реакции не только в случае наличия элементов в количествах, соответствующих стехиометрии MAX-фазы, т. е. Cr:Ga:C=2:1:1, но и для всех возможных соотношений. Каждой фазе был приписан соответствующий набор из трёх цифр, первая из которых означает количество атомов хрома в формульной единице соединения, вторая – количество атомов галлия, третья – углерода. Например, фазе Cr 7 C 3 был приписан набор 703, фазе Cr 3 Ga– 310. Таким образом, список соединений был преобразован в список наборов чисел, обращение к которым в программном коде сводилось к обращению к определённым элементам матрицы. Каждый набор из трёх цифр также имел порядковый номер, которому соответствовала энтальпия кодируемой фазы. Потребность обращения к каждому типу входящих в фазу атомов отдельно была обусловлена необходимостью расчёта атомарного баланса в уравнении и поиска наибольших коэффициентов при всех фазах в правой части уравнения. Реализация последнего в программном коде основывалась на идее проверки, возможно ли формирование какой либо фазы в правой части из остатков свободных атомов. С помощью введения таких дополнительных внутренних циклов было обнаружено, что в некоторых случаях коэффициенты при фазах в правой части уравнения действительно отличались от единиц, т. е. от того, как это было записано в начале при описании общего вида уравнения реакции (1).

В данной работе было рассмотрено три различных типа реакций. Типы определяются количеством различных конкурирующих фаз. Первый тип содержит С ₇ ¹ = 7 различных реакций, отличающихся конкурирующей фазой; второй тип содержит С ₇ ² = 21 различную реакцию, каждая из которых содержит уникальную пару конкурирующих фаз; третий тип содержит С ₇ ³ = 35 различных реакций, каждая из которых содержит уникальную тройку конкурирующих фаз. Кроме того, каждая реакция может быть записана без MAX-фазы в правой части уравнения.

Так как изменяемым параметром в расчётной модели было соотношение количеств трёх различных чистых элементов, было решено представлять результаты в виде тернарных диаграмм. А именно, в виде набора из трёх тернарных диаграмм для каждого из случаев (для каждой из стрелок схемы 1). Ниже приведены результаты только для первого и второго типов реакций при наличии МАХ-фазы в правой части уравнения (рис. 2, 3).

Каждая точка на тернарных диаграммах рис. 2 соответствует одному определённому соотношению Cr:Ga:C. Для этого соотношения были рассчитаны и сопоставлены 7 энтальпий. Затем определялось наиболее отрицательное значение и точка окрашивалась в цвет, соответствующий конкурирующей фазе, образование которой приводит к наибольшему высвобождению энергии. На диаграммах легко наблюдаются области и их границы. Это позволяет нам судить, например, об экспериментальной ошибке в соотношении количеств элементов: сравнивая ожидаемые и полученные конкурирующие фазы, можно определить, какой элемент был взят в избытке. На третьей диаграмме (рис. 2, в ) показана разница между теплотами образования двух наиболее термодинамически выгодных конкурирующих фаз. Примечательно, что лидирующие фазы одинаковы, они только меняют свои области.

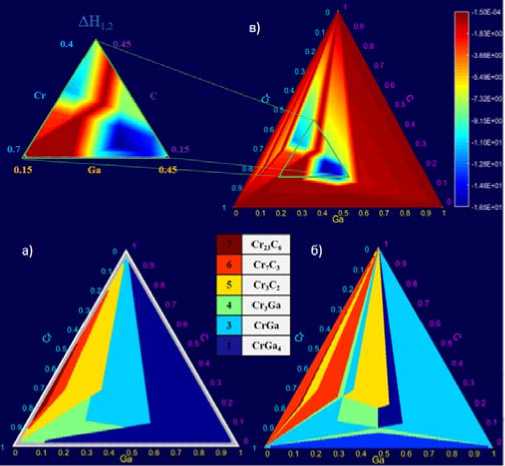
Рис. 2. Диаграммы номеров наиболее выгодных конкурирующих фаз

(в случае образования MAX-фазы и одной конкурирующей фазы): а – первый кандидат; б – второй кандидат; в – разница между эффективными теплотами образования (кДж/моль*атом) двух наиболее термодинамически выгодных конкурирующих фаз

• Fig. 2.    Diagrams of the numbers of the most favorable competing phases

(in the case of the formation of the MAX-phase and one competing phase):

(bottom left) the first candidate; (bottom right) the second candidate; (top right) the difference between the effective heat of formation (kJ/mol*atom) of the two most thermodynamically favourable competing phases

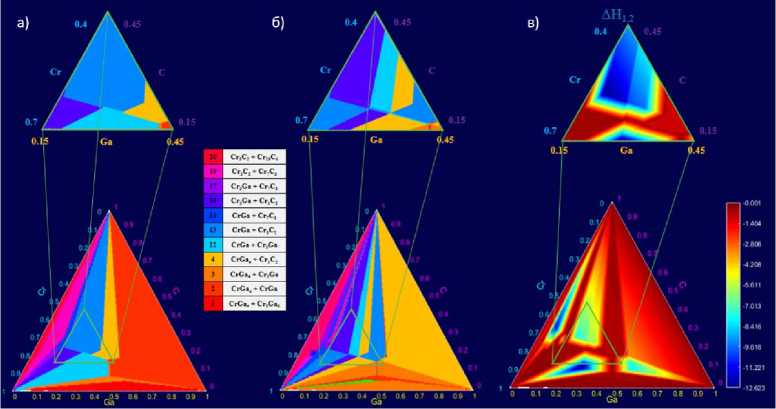
Рис. 3. Диаграммы номеров наиболее выгодных конкурирующих фаз (в случае образования MAX-фазы и двух конкурирующих фаз): а – первый кандидат; б – второй кандидат; в – разница между эффективными теплотами образования (кДж/моль*атом) двух наиболее термодинамически выгодных конкурирующих фаз

• Fig. 3.    Diagrams of the numbers of the most favorable competing phases

(in the case of the formation of the MAX-phase and two competing phases): (bottom left) the first candidate; (bottom right) the second candidate; (top right) the difference between the effective heat of formation (kJ/mol*atom) of the two most thermodynamically favourable competing phases

То же самое было сделано в случае двух конкурирующих фаз (рис. 3), т. е. для второго типа реакций. Видно, что группа лидирующих фаз снова остаётся прежней: CrGa, Cr 3 Ga, Cr 3 C 2 , в этом случае мы просто имеем дело с их комбинациями.

Согласно модели эффективной теплоты образования [2], одним из наиболее значимых факторов, влияющих на образование фаз, является число атомов в элементарной ячейке: чем больше число атомов в элементарной ячейке, тем более затруднено образование фазы (табл. 1).

Количество атомов в элементарных ячейках различных фаз

Таблица 1

Cr 3 Ga 21 атом в элементарной ячейке	CrGa 92 атома в элементарной ячейке	Cr 3 C 2 20 атомов в элементарной ячейке	Cr 2 GaC 18 атомов в элементарной ячейке
о® Л? *^*		•>	о ^Н ^ О
	Т**5бб^>'е О 4W«?0 ’
		5»№	о a--t^-^

Таблица 2

Ориентационные соотношения и плотность совпадающих узлов на границе раздела между МАХ-фазой Cr2GaC и MgO [3; 4]

Интерфейс	u11v11w11	U12v1 2w12	u21v21w21	u22v22w22	h1k1l1	h2k2l2	Плотность совпадающих узлов, R
MgO||Cr2GaC	[011]	[020]	[10-1]	[200]	(–11-1)	(001)	0.0418
MgO|| CrGa	[0-11]	[11-2]	[–1.578 – 2.989 1.071]	[4.61 1.49 4 0.0]	(–11-1)	(–5.09 2.989 0.507)	0.0545
MgO|| Cr3Ga	[0-11]	[11-2]	[010]	[001]	(–11-1)	(001)	0.0887

Кроме того, рассмотрение возможной границы раздела CrGa и поверхности оксида магния MgO(111) по методу решёток совпадающих узлов выявляет предпочтительность фазы Cr 3 Ga по сравнению с CrGa (табл. 2).

Заключение

При формировании магнитных тонких плёнок MAX-фаз существуют только три термодинамически наиболее выгодные фазы: CrGa, Cr 3 Ga, Cr 3 C 2 .

Хотя энтальпия образования CrGa наиболее отрицательна, в соответствии с методом решёток совпадающих узлов более вероятно образование фазы Cr3Ga, имеющей меньше атомов в элементарной ячейке, что подтверждено экспериментально [15].