Прогнозирование падения финансовых рынков в программной среде GRETL

В настоящее время в связи с глобализацией экономики одной из актуальных проблем является построение эффективного механизма управления социально-экономическим развитием, позволяющего увязать текущие процессы обеспечения всех сфер жизни с будущими долгосрочными перспективами. Как показывает мировой опыт, наилучшим инструментом для исследования сложных социально-экономических систем и принятия макроэкономических решений является эконометрическое моделирование.

Основным этапом эконометрического моделирования является выбор модели. Наибольшее применение в эконометрике нашли линейные модели.

Многие зарубежные авторы для моделирования финансовых рынков используют динамическую панельную модель Panel Tobit с гетероскедастичностью для генерации точечных прогнозов и прогнозов плотности для большого сечения коротких временных рядов. Полностью байесовский подход позволяет гибко оценивать распределение поперечных сечений разнородных коэффициентов, а затем использовать это распределение для построения байесовских прогнозов для отдельных временных рядов. Панельная модель с ограниченными зависимыми переменными с ненаблюдаемыми индивидуальными эффектами является общей структурой данных, но не изучена в литературе по прогнозированию.140

Также существует мнение, что можно использовать с тохастическую динамическую модель экономического цикла, которая учитывает монетарные шоки в экономике и их влияние на волатильность.

Другая, не менее известная модель - ARCH-модель . Появление ARCH-моделей в восьмидесятых годах прошлого века повлекло за собой беспрецедентный рост количества разработок в сфере финансовой эконометрики. Данная модель впервые была предложена в работе R.F. Engle141.

В настоящий момент для анализа волатильности биржевых индексов на фондовых рынках можно использовать как раз модели семейства Generalised ARCH (GARCH) . В частности, авторы статьи142 по результатам своего исследования пришли к выводу о том, что, например, модель Power

• ¹⁴⁰     LAURA LIU, HYUNGSIK ROGER MOON, FRANK SCHORFHEIDE. FORECASTING WITH A PANEL TOBIT MODEL // ЭЛЕКТРОННЫЙ РЕСУРС // NATIONAL BUREAU OF ECONOMIC RESEARCH, MASSACHUSETTS     AVENUE     CAMBRIDGE,     DECEMBER     2019.     URL:

(ДАТА ОБРАЩЕНИЯ: 22.03.2020)

• ¹⁴¹    Engle R. F.(1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United

  Kingdom       inflation       //       Econometric,       50       (4),       987–1007.       URL

  https://www.econometricsociety.org/publications/econo metrica/1982/07/01 /autoregressive-conditional-

• heteroscedasticity-estimates

  • ¹⁴²    Федорова Е.А., Панкратов К.А. Моделирование волатильности фондового рынка в период кризиса / Финансовая аналитика: проблемы и решения. 2011. URL: https://cyberleninka.ru/article/n/modelirovanie-volatilnosti-fondovogo-rynka-v-period-krizisa (дата обращения: 22.03.2020)

ARCH (PGARCH) наиболее подходит для прогнозирования волатильности индекса ММВБ, особенно в периоды нестабильности и финансовых кризисов.

Также стоит добавить, что наиболее информативной литературой по эконометрике, по нашему мнению, на сегодняшний день является книга Кристофера Доугерти «Введение в эконометрику», «Эконометрика» Наума Кремера и «Эконометрика» Фумио Хайяши.

В качестве модели была выбрана модель множественной линейной регрессии, так как в модели присутствуют два и более регрессора. При выполнении определенных условий метод наименьших квадратов дает несмещенные и эффективные оценки b1 и b2. По этой причине МНК является наиболее популярным при исследовании методов регрессионного анализа.

МНК-оценка выбирает коэффициенты регрессии так, чтобы оцененная линия регрессии была близка настолько, насколько возможно к наблюдаемым данным, где близость измеряется суммой квадратов ошибок, которые возникают при предсказании Y при заданных X.

Данная проектная работа была выполнена посредством возможностей программы Gretl. Ориентация на данную программу была обусловлена тем, что данный он является бесплатным программным продуктом, который, с одной стороны, доступен любому пользователю, а с другой обладает достаточно обширными возможностями для анализа данных и проведения эмпирических исследований.

Результирующей переменной в нашем случае является ВВП – это один из ключевых показателей, в количественном отношении выражающий развитие экономики.

В качестве факторов, способных оказать воздействие на ВВП, были отобраны следующие показатели: объем сделок (торгов), уровень инфляции и биржевой индекс PTC.

Объем выборки составляет 10 лет: с 2010 по 2019 гг.

Информационной базой работы являются данные, содержащиеся на официальном сайте «Федеральной службы государственной статистики», «Московской биржи», а также других Интернет-ресурсах.

Перейдем к непосредственно к результатам нашего решения, сопровождая их при этом необходимыми выводами.

Наша работа началась с создания рабочего листа с исходными данными в Excel. Далее данные из этого листа были импортированы в Gretl.

Далее посредством программы нами была выведена корреляционная матрица. То, в каком виде она была сформирована, можно наблюдать ниже (таблица 1).

Таблица 1. Коэффициенты корреляции, наблюдения 2010 - 2019 5% критические значения (двухсторонние) = 0,6319 для n = 10

ВВП	Объем сделок	Инфляция	PTC
1,0000	0,5660	-0,4489	-0,4034	ВВП
	1,0000	-0,7858	0,2765	Объем сделок
		1,0000	-0,4337	Инфляция
			1,0000	PTC

Определитель матрицы близок к нулю (0,08735). Близость определителя к нулю делает уравнение регрессии менее надежным и говорит о наличии мультиколлинеарности между экзогенными факторами.

Рассмотрим влияние каждого показателя в отдельности. Зависимым показателем будет выступать ВВП, а независимыми переменными будут представленные выше показатели.

Для определения влияния на ВВП всех отмеченных ранее факторов с помощью Gretl была построена модель множественной регрессии с использованием метода наименьших квадратов. (Таблица 2)

Таблица 2. Модель множественной регрессии, зависимая переменная:

ВВП

	Коэффициент	Ст. ошибка	t-статистика	P-значение
const	115022	45343,3	2,537	0,0443 **
V сделок	1,10101	0,888800	1,239	0,2617
Инфляция	-2305,77	2138,01	-1,078	0,3223
PTC	-40,5686	14,0744	-2,882	0,0280 **

Наличие двух звездочек говорит о значимости коэффициента на 5 %-ном уровне. Отсутствие звездочек говорит о незначимости коэффициента на 10 %-ном уровне.

Согласно вышеприведенной таблице, статистически значимым (и позволяющим отвергнуть нулевую гипотезу) считается результат, р-значение которого равно уровню значимости или меньше его. Это, как правило, обозначается следующим образом: p ≤ 0,05 (5%). Исключая константу - ВВП, наибольшее р-значение получено для переменных инфляция и объем сделок, значения больше 0,05, следовательно, данные переменные статистически не значимы. Так наиболее значимым фактором является индекс РТС, имеющим р-значение 0,0280 (около 3%).

Для определения влияния на него всех отмеченных ранее факторов в совокупности было построено уравнение множественной регрессии, представленное в таблиц

Таким образом, исходя из полученных данных, линейная трехфакторная модель регрессии имеет следующий вид:

Y= 115 022+1,10101x1-2305,77x2-40,5686x3

С помощью критерия Фишера оценим качество регрессионной модели в целом. Для этого в основном меню программы Gretl было выбрано “Инструменты / Критические значения / Фишера” и введены нужные параметры распределения. Программа вывела следующие данные:

• •    Степень свободы 1=m

• •     Ст. свободы 2 = n-m-1, где n - количество наблюдений, m

  • -    количество факторов

  • •      F(3, 6)

  • •     Правосторонняя вероятность = 0,05 (а)

  • •     Дополняющая вероятность = 0,95

  • •     Критическое значение = 4,75706 (Fфакт)

При α = 0,05 Fтабл (3, 6) = 5,017569, следовательно, Fтабл >Fфакт. Т.е.

нулевая гипотеза о незначимости регрессии в целом отвергается на уровне значимости α = 0,05, коэффициенты одновременно при всех регрессорах не равны нули, что подтверждает совместно влияние факторов на зависимую переменную.

Следующим этапом анализа является оценка параметров регрессионной модели. Для выполнения данной задачи в конкретном случае используется метод наименьших квадратов, основанный на минимизации разницы между истинными значениями независимой переменной и ее оценками.

Среднее зав. перемен 80140,87 Ст. откл. зав. перемен 19219,82

Сумма кв. остатков 9,48e+08 Ст. ошибка модели 12566,56

R-квадрат       0,715001      Испр. R-квадрат    0,572502

F(3, 6)         5,017569        Р-значение (F)     0,044874

Лог. правдоподобие -106,0232 Крит. Акаике      220,0464

Крит. Шварца      221,2568 Крит. Хеннана-Куинна 218,7187

Исключая константу, наибольшее р-значение получено для переменной 3 (биржевой индекс РТС). Данная модель обладает достоверностью на уровне 0,7150, поскольку значение R-квадрат = 0,7150, это означает, что данная регрессионная модель описывает 71,5% последствий падения фондового рынка, а 29,5 % - подпадает под влияния других причин, не вошедших в модель.

Информационный критерий Хеннана-Куина используется для сравнения моделей с разным числом параметров, когда требуется выбрать лучший набор независимых переменных. Он является альтернативой информационным критериям Акаике и Шварца. При прочих равных условиях следует предпочитать модель, в которой значение критерия более низкое (что и было сделано при помощи программы Gretl).

Также были проведены тесты на наличие автокорреляции, гетероскедастичности и ARCH-процессов. Результаты получились следующие:

• 1.    LM тест на наличие автокорреляции до порядка 4 -

• Нулевая гипотеза: автокорреляция отсутствует

  Тестовая статистика: LMF = 0,809342

• 2.    LM тест на наличие автокорреляции до порядка 2 -

• Нулевая гипотеза: автокорреляция отсутствует

  Тестовая статистика: LMF = 1,40391

• 3.    Тест на наличие ARCH процессов порядка 1 -

• Нулевая гипотеза: ARCH процессы отсутствуют

  Тестовая статистика: LM = 0,522397

• 4.    Тест на наличие ARCH процессов порядка 3 -

• Нулевая гипотеза: ARCH процессы отсутствуют

  Тестовая статистика: LM = 1,58472

р-значение = P(F(4, 2) > 0,809342) = 0,617917, следовательно, нет оснований для отклонения нулевой гипотезы.

р-значение = P(F(2, 4) > 1,40391) = 0,345226, следовательно, нет оснований для отклонения нулевой гипотезы.

р-значение = P(Хи-квадрат(1) > 0,522397) = 0,469821, следовательно, нет оснований для отклонения нулевой гипотезы.

р-значение = P(Хи-квадрат(3) > 1,58472) = 0,66286, следовательно, нет оснований для отклонения нулевой гипотезы.

Таблица 3. Тест Вайта (White) на гетероскедастичность МНК, использованы наблюдения 2010-2019 (T = 10)

	Коэффициент	Ст. ошибка	tстатистика	P-значение
const	-4,41148e+09	3,43686e+09	-1,284	0,2895
V сделок	35249,3	117081	0,3011	0,7830
Инфляция	-8,19155e+07	1,15205e+08	-0,7110	0,5284
PTC	5,65094e+06	4,43052e+06	1,275	0,2920
sq_Vсделок	-0,280725	1,82576	-0,1538	0,8876
sq_Инфляция	1,11046e+07	8,91257e+06	1,246	0,3012
sq_PTC	-2045,30	1649,53	-1,240	0,3031

Неисправленный R-квадрат = 0,600173 Тестовая статистика: TR^2 = 6,001730, р-значение = P(Хи-квадрат(6) > 6,001730) = 0,4229960, что говорит об отсутствии автокорреляции в остатках.

Заключительным этапом в данной работе является составление прогноза для нашей модели. Результаты прогноза по исходным данным представлены на рисунках ниже.

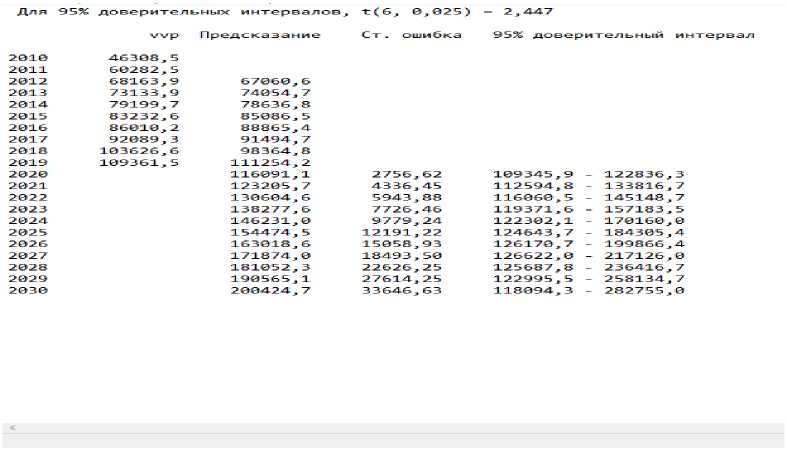
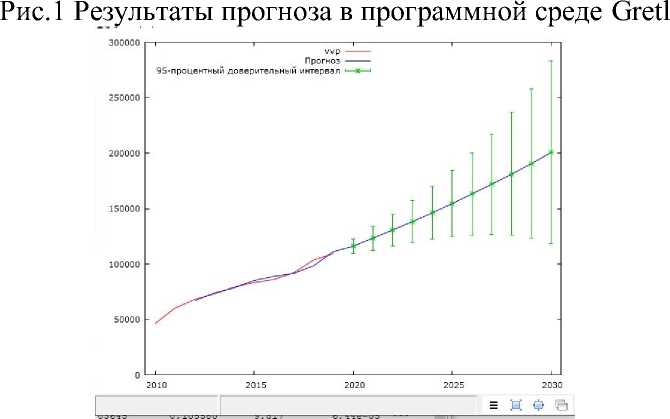
Рис.2 Результаты прогноза (график) в программной среде Gretl

Как можно заметить из данных графы “Предсказание”, наблюдается положительная динамика результирующей переменной, т.е. ВВП.

Таким образом, полученная модель в целом характеризовалась как

адекватная. Было выявлено, что между положительная линейная зависимость.

переменными существует

Согласно   результатам

корреляционно

-

регрессионного анализа,

было выявлено,

результативный показатель (ВВП) наибольшее влияние

биржевой индекс РТС. незначимыми.

Оставшиеся коэффициенты

что на оказывает оказались