Прогнозирование показателей качества жизни методами нелинейной динамики

Проблема разработки прогнозов социально-экономического развития регионов России особенно остро проявилась в условиях финансово-экономического кризиса. Качество и уровень жизни населения являются одними из основных факторов, определяющих демографическую, социальную и экономическую стабильность в обществе.

Под качеством жизни понимается категория, включающая в себя сочетание ряда условий, характеризующихся физическим, психологическим и социально-экономическим благополучием населения региона и возможностями развития отдельной личности [2].

В работе [3, С. 368] предложена методология прогноза социально-демографического развития России на перспективу до 2030 года, включающая программу социально-демографических целей, на достижение которых ориентирован экономический рост, и взаимосвязанный комплекс социально-демографических проблем, требующих разрешения в течение периода прогнозирования.

Вычленение ключевых социально-демографических проблем базируется на оценке сложившейся ситуации состояния и динамики основополагающих социально-демографических процессов: численности населения, масштабов естественной убыли населения; уровня материального обеспечения населения; величины прожиточного минимума, реальных масштабов бедности; масштабов безработицы и других [3, С. 368-369].

Для целей прогнозирования в настоящее время широко используются экономикоматематические модели эконометрического типа (факторные и структурные) [4], основным достоинством которых является внутренняя согласованность экономических показателей, характеризующих процесс, за счет учета в моделях различных существенно важных для объекта исследования взаимосвязей [5].

Небольшое количество точек временного ряда показателей рассматриваемого процесса является неким препятствием для построения адекватной экономикоматематической модели. Использование для прогнозирования методов нелинейной динамики позволяет достроить временной ряд на определенном интервале времени в будущем, учитывая при этом время достоверного прогноза для данного ряда.

Прогноз будущих значений временного ряда в работе производится с помощью модернизированного метода Херста [6-7]. Алгоритм построения следующей точки ряда при прогнозе заключается в переборе всех предполагаемых значений исследуемой величины с определённым шагом и вычислении для ряда, содержащего достроенную точку, функции R(т)/S(т) и последующем её сравнением с R(т)/S(т) функцией исходного ряда. Выбирается точка, дающая для прогнозируемого значения показателя такую же (или наиболее близкую) функцию Херста, какая была и для исходного ряда. Следовательно, и Н*(т) для достроенного на одну точку ряда должна совпасть с Н*(т) для ис ходного ряда:

где R(t) - функция абсолютного размаха;

S(t) - стандартное отклонение;

R(t)/S(t) - функция нормированного размаха; т - временной масштаб.

. (1)

Затем берётся следующая точка, рассматривается следующий временной промежуток (через год) и производятся те же действия. Аналогично поступают и для следующих точек.

Если проанализировать поведение Н* от временного масштаба т , то по его постоянству можно классифицировать ряд как фрактальный или нефрактальный. Если и* л 5

H*=const на любом временном масштабе т и при этом        , то ряд можно считать статистически фрактальным с фрактальной размерностью В = 2-Н* и корреляционной функцией:

z^ гч2,Н*—1 -I

С = 2     -1. (2)

Если H*=const и при этом его значение 0,5, то ряд случаен, его фрактальная размерность имеет значение D =1,5, а корреляционная функция так же, как и у фрактального ряда, не зависит от времени и равна 0. То есть при H*=const справедливы формулы для определения фрактальной размерности D и корреляционной функции C .

Если же функция Н*( т) испытывает скачок при каком-либо значении т* , это означает, что существует некоторый характерный временной масштаб изменения фрактальной размерности D. При этом для периодических функций будет наблюдаться переход от Н* >0,5 к Н* <0,5. Для рядов с локальной антиперсистентностью и глобальным поддержанием тенденции Н*( т) будет испытывать обратный скачок. В этом случае можно выделить характерное время изменения характера поведения исследуемого параметра, равное т* , при котором и произошёл скачок.

Таким образом, по поведению Н*(т) можно классифицировать временные ряды, как статистически фрактальные, случайные, периодические, и выделить ещё один тип -с глобальной персистентностью, который характерен для функций роста или убывания.

Показатель Херста H указывает на поддержание повышающей или понижающей тенденции, если H >0,5. Значения H <0,5 указывают на склонность к смене тенденции, если в прошлом был рост - в будущем произойдёт спад, и наоборот.

В результате анализа было выяснено, что более рационально применять данный метод к темпам изменения показателей, так как исследуемые временные ряды темпов имеют более сложную фрактальную структуру, чем временные ряды самих показателей.

В таблице представлены результаты расчетов фрактальных характеристик временных рядов по следующим показателям: доля населения с доходами ниже прожиточного минимума и уровень безработицы в Российской Федерации1.

Таблица

Фрактальные характеристики временных рядов показателей качества жизни населения Российской Федерации

Показатели	Доля населения с доходами ниже ПМ, % к предыдущему году	Уровень безработицы, % к предыдущему году
Показатель Херста H	0,67±0,17	0,61±0,20
Фрактальная размерность D	1,33±0,34	1,39±0,45
Корреляционная функция C	0,266	0,159

На рис. 1 приведен долгосрочный прогноз по темпам роста доли населения с доходами ниже прожиточного минимума в Российской Федерации, на рис. 2 – по отношению к базовому периоду. Прогнозируемые точки вычислены с использованием описанного выше фрактального метода.

%

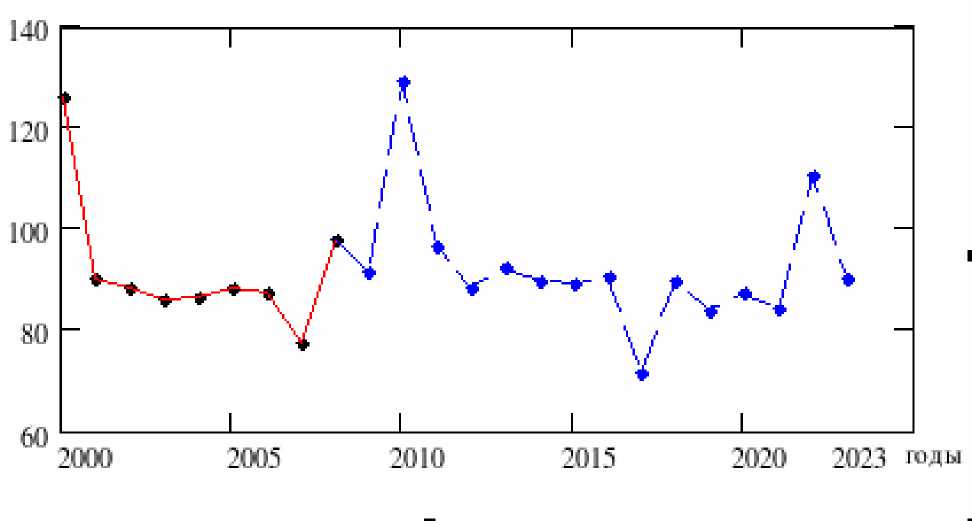
Рис. 1. Прогноз темпов роста доли населения с доходами ниже прожиточного минимума в Российской Федерации, % к предыдущему году.

В 2010 г. по данным прогноза наблюдается увеличение доли населения с доходами ниже прожиточного минимума (рис. 2), что можно было бы объяснить сложившимися экономическими отношениями в условиях кризиса, а значит и самоподобием временного ряда, определяющим его фрактальность.

%

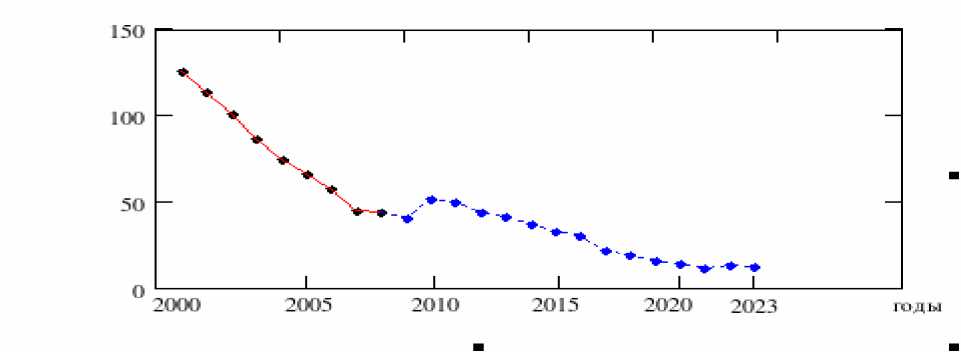
Рис. 2. Изменение доли населения с доходами ниже прожиточного минимума, % к 1999 г., прогноз до 2023 года.

Аналогичные расчеты с использованием методов нелинейной динамики проведены для уровня безработицы в Российской Федерации (рис. 3 и 4). Уровень безработицы в 2010 г. останется приблизительно на уровне 2009 г., а в 2011 году будет наблюдаться снижение данного показателя.

Прогноз остается справедливым до тех пор, пока фрактальные свойства временного ряда, соответствующие сложившейся структуре экономических отношений, не изменятся.

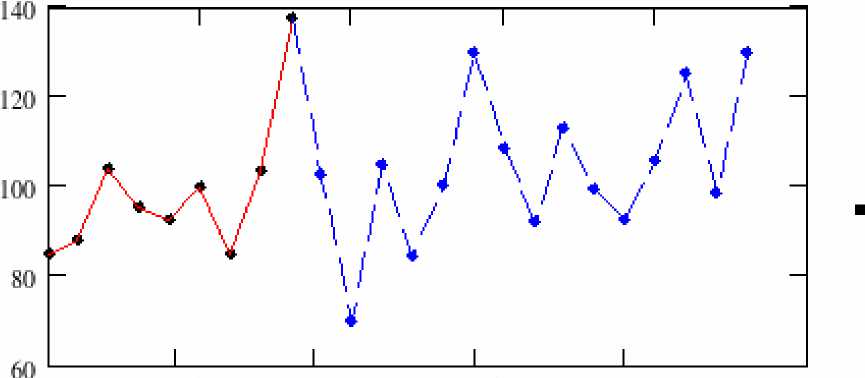
2001      2005       2010         2015        2020            годы

Рис. 3. Прогноз темпов роста уровня безработицы в Российской Федерации, % к предыдущему году.

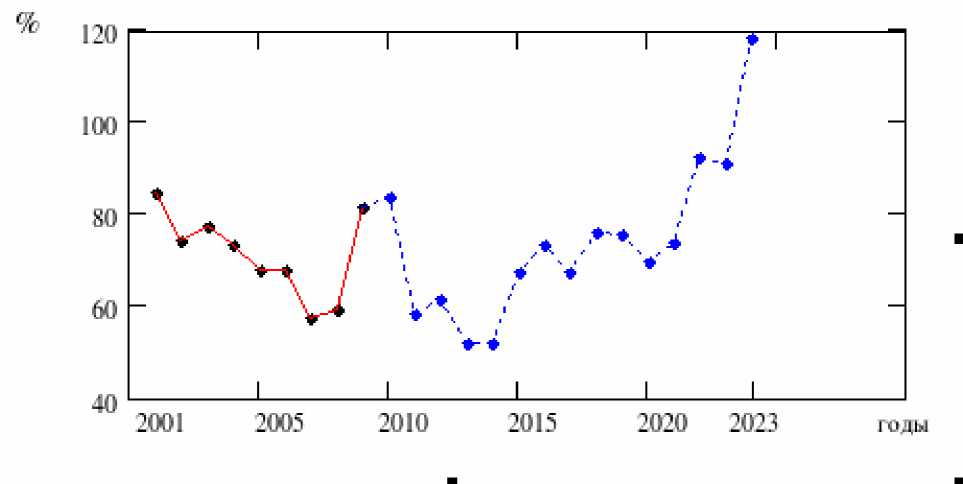
Рис. 4. Прогноз уровня безработицы, % к 2000 г.

С помощью фрактального подхода в рамках нелинейной динамики разработана методика анализа и прогнозирования поведения временных рядов экономических систем. Если устремить длину исходного ряда к бесконечности, и при этом окажется, что ряд является статистически фрактальным, то возможно его неплохое (статистически) предсказание на интервалы времени, существенно превышающие длину самого ряда. Используемый в работе метод Херста можно применять с хорошей точностью даже к относительно небольшим массивам данных.

* *

• 1.    Быстрай Г.П., Николаева Е.В., Журкина А.В. Рыбалко А.А. Валютные рынки: математическое моделирование хаотических состояний. Препринт. – Екатеринбург: УрО РАН, 2001. – 61 с.

• 2.    Комплексная методика диагностики качества жизни в регионе / Под ред. акад. РАН А.И. Татаркина, д-ра экон. наук, проф. А.А. Куклина. 2-е изд., испр., доп. – Екатеринбург: Институт экономики УрО РАН, 2010. – 136 с.

• 3.    Методические рекомендации и материалы по разработке прогноза научно-технологического и социально-экономического развития России до 2030 года (Материалы секций Координационного

  совета Российской академии наук по прогнозированию). – М.: ИНЭС, 2010. – 542 с.

• 4.    Методы народнохозяйственного прогнозиро-вания/Под ред. акад. Н.П.Федоренко, акад. А.И. Анчишкина, д.э.н. Ю.Я. Яременко. – М.: Наука, 1985. – 472 с.

• 5.    Трисеев Ю.П. Долгосрочное прогнозирование экономических процессов (системные методы). – Киев: Наукова думка, 1987. – 134 с.

• 6.    Федер Е. Фракталы: Пер. с англ. – М.: Мир, 1991. – 254 с.

• 7.    Hurst H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng., 1951.