Прогнозирование показателей научного потенциала региона на основе генетического алгоритма

Концептуально прогнозирование связывают с появлением потребности в решении поиска институционального и структурного направлений научно-инновационного развития территориального образования. При этом исходят из анализа этой потребности на основе существующих теоретико-методологических подходов решения задач прогнозирования. Основным постулатом является то, что прогнозирование рассматривается как функциональная часть системы управления, основная задача которой определяется упреждающей ориентацией системы управления на возможные изменения состояния и среды объекта управления.

Теоретический анализ

Как известно, в основу методологии прогнозирования положены принципы системности, комплексности, многовариантности, при этом можно использовать два подхода. Первый основан на прогнозировании направлений развития системы и последующей оценкой ресурсов, необходимых для их реализации. В этом случае основополагающим является создание системы управления, адекватной научно-инновационному развитию региона. В основе второго подхода лежит разработка прогноза развития инновационного ресурса с определением последующих возможных направлений научно-инновационного развития. При данном подходе акцент делается на создание механизма программного управления научно-инновационным развитием территории.

Прогнозирование научно-инновационного развития региона относится к классу задач, связанных с поиском оптимального решения комбинаторного типа, и в настоящее время проводятся интенсивные исследования в области разработки новых аналитических технологий. При этом особое внимание уделяется генетическим алгоритмам. Генетические алгоритмы – это специальная технология для поиска оптимальных решений, которая успешно применяется в различных областях науки и бизнеса. В этих алгоритмах используется идея естественного отбора. Генетические алгоритмы часто применяются совместно с нейронными сетями, позволяя создавать предельно гибкие, быстрые и эффективные инструменты анализа данных [1].

Стратегия поиска оптимального решения в генетических алгоритмах опирается на гипотезу селекции: чем выше приспособленность особи, тем выше вероятность того, что у потомков, полученных с ее участием, признаки, определяющие приспособленность, будут выражены еще сильнее [2]. «Следует отметить, что классический генетический алгоритм находит глобальный экстремум в вероятностном смысле. И эта вероятность зависит от числа особей в популяции ...при оптимизации сложных многоконтурных и многосвязных систем регулирования и аналогичных систем с нейроконтроллерами генетические алгоритмы с достаточно высокой вероятностью находят глобальный экстремум» [3].

Вместе с тем специалисты выделяют недостатки генетического алгоритма. Это случайный отбор, что не гарантирует получения лучшего результата, нахождение оптимального решения только внутри заданного диапазона поиска, что связано с расширением его границ, вероятностных характеристик поиска функции приспособленности. По мнению В.В. Шишкина, метод генетического алгоритма не обеспечивает стопроцентного достижения глобального экстремума целевой функции, но дает в приемлемое время «псевдооптимальное» решение [4].

Теоретико-методической основой процесса прогнозирования является множество методов, описывающих будущее, каждый из которых может применяться для решения конкретной задачи. Так, формализованные методы используются, как правило, для прогнозирования структурированных задач и наличия достаточно обширной информационной базы. Что касается прогнозирования класса неструктурированных задач, то здесь широко используется методологическая база интуитивных (экспертных) методов, что согласуется с процессом научно-инновационного развития. Они применяются в условиях отсутствия достаточно представительной и достоверной статистики характеристики объекта, неопределенности среды функционирования при средне-, долгосрочном прогнозировании новых объектов [5, с. 149]. Однако те и другие методы имеют определенные ограничения при прогнозировании развития инновационных систем, в связи с этим растет потребность в использовании генетического алгоритма.

В настоящее время методологией и теорией разработки генетического алгоритма для решения экономических задач занимаются многие ученые различных научных школ, и считается, что развитие методологии генетического алгоритма обеспечит достаточно эффективное его использование для задач прогнозирования сложных систем.

Методика

В рамках данной работы рассматривается применение генетического алгоритма для прогнозирования показателей научного потенциала региона на примере Республики Бурятия.

Процедура разработки прогноза развития научного потенциала включает:

• 1)    постановку процедурных вопросов прогнозирования научно-инновационного развития республики;

• 2)    формирование базы данных, выбор и обоснование показателей, отражающих состояние, эффективность использование инновационного ресурса, результаты развития субъектов инновационной системы;

• 3)    выбор методов прогнозирования и обработки информации;

• 4)    разработку генетического алгоритма :

• -    построение модели и выбор зависимости на основе статистических критериев качества;

• -    определение архитектуры эволюционного поиска;

• -    определение схемы работы простого генетического алгоритма;

• -    апробацию работы генетических алгоритмов и расчет прогнозных значений параметров научного потенциала;

• 5)    анализ и интерпретацию результатов прогнозирования.

Процедурные вопросы прогнозирования непосредственно связаны с формированием цели, задач и объекта прогнозирования. Исходя из цели и задач прогнозирования, мы предлагаем подход разработки прогноза научного потенциала, который позволит определить возможные варианты направлений научного развития республики. При разработке прогноза используется оценка динамических рядов показателей, характеризующих уровень развития научного потенциала республики. Состав локальных показателей состоит из ресурсных и результативных характеристик развития республиканской науки. Ресурсная составляющая включает показатели имеющегося кадрового потенциала исследователей, подготовки высококвалифицированных кадров, технической базы проведения научных исследований и затрат на проведение научно-исследовательских работ. С целью выявления функции приспособленности особей популяции использовался корреляционнорегрессионный анализ статистических данных отобранных показателей.

Экспериментальная часть

Для анализа динамики основных показателей развития научного потенциала взят период с 1995 по 2008 г. Однако существует проблема недостаточности статистической информации. В связи с этим следует исходить из предпосылок регрессионного анализа, а само моделирование - из развития научного потенциала при помощи построения эконометрических моделей в виде системы уравнений. Для этого на первоначальном этапе производили поиск зависимых переменных, определение уравнений зависимости по множеству исходных переменных, выбор среди них значимых и определение окончательной зависимости. Отбор наиболее существенных факторов, выбор формы связи между результативными и факторными показателями, а также выявление функции приспособленности проводились на основе корреляционно-регрессионного анализа, одним из условий которых является отсутствие мультиколлинеарности .

Итеративным путем осуществлялось построение зависимостей между результирующими и существенными факторами, на основе которых строилась модель принятия решений. Эконометрическая модель в задаче прогнозирования реализуется как рекурсивная модель, отражающая последовательность и взаимосвязь основных индикаторов развития научного потенциала, и представляет собой набор регрессионных моделей, в которых одни и те же независимые переменные одновременно играют определенную роль.

В качестве экзогенных переменных в момент времени t взяты следующие переменные:

• Y 1 t - доля научно-исследовательских работ (НИР) в % к ВРП;

• Y ₂ t - численность персонала НИР на 10 тыс. занятых в экономике, чел.;

• Y 3 t - доля исследователей в общей численности работников, занятых научными исследованиями и разработками;

• Y 4 t - доля исследователей высшей квалификации.

Совокупность данных переменных характеризует блок взаимосвязанных показателей развития ресурсов республиканской науки.

В качестве эндогенных переменных в момент времени t взяты показатели: доля активной части ОФ НИР, в %; доля государственных средств в науку, в %; доля исследователей технических наук; доля исследователей технических наук высшей квалификации; доля аспирантов по техническим наукам; доля исследователей сельскохозяйственных наук; доля исследователей сельскохозяйственных наук высшей квалификации; доля аспирантов сельскохозяйственных наук; доля приема в аспирантуру от выпуска специалистов дневного обучения; доля выпуска аспирантов с защитой.

Модель строилась исходя из причинно-следственных связей переменных y_u ^ Y ^ Y ^ Y

В результате получена следующая система уравнений:

Y t = 0,314 + 0,012 Y 2 1 ( x i ) - 3,84 x 2

Y _{2 1} =- 96,83 + 51,83 Y _{3 1} ( x _n) + 46,97 x ₁₂ + 0,66 x ₁₃ + 20,04 Y _{4 1} ( x ₁₄)

Y , t ( x 11 ) = 0,579 + 0,668 Y„ , ( x _m) + 0,363 Y ,2 , ( x _n2)

‘ Y 31 1 ( x 111 ) = - 0,096 + 0,865 x _lm + 1,027 x _m2

Y _{i2 1} ( x ₁₁₂) = — 0,055 + 0,676 x ₁₁₂₁ + 2,578 x ₁₁₂₂

Y 41 ( x 14 ) = 0,24 + 0,603 x 141 + 0,82 x 14 ₂

Анализ статистических характеристик модели показал, что она в целом адекватно описывает развитие научного потенциала (табл. 1).

Построенная модель позволяет использовать главные зависимости компонентов в качестве функций приспособленности для разработки генетических алгоритмов.

Из существующих в настоящее время нестандартных архитектур эволюционного поиска для решения поставленной задачи выбрана стратегия эволюционного поиска с миграцией. На первом этапе выполняется метаэволюция, т.е. создание множества популяций и реализация на их основе эволюционного поиска. Он осуществляется путем объединения хромосом из различных популяций.

Таблица 1

Статистические характеристики рекурсивной модели развития научного потенциала

Статистические характеристики	Номер регрессионного уравнения
	У 1t	У 2 t	У 3 t	У 31 t	У 32 t	У 4 t
Коэффициент детерминации ( R2 )	0,87	0,80	0,77	0,80	0,79	0,84
Наблюдаемое значение F- критерия Фишера ( Fнабл. )	19,92	4,49	4,94	68,64	9,85	14,51
Табличное значение F- критерия Фишера ( Fтабл. )	12,98	3,48	3,88	12,98	6,93	6,93
Наблюдаемое значение t- критерия Стъюдента ( tнабл. )	4,76	2,59	2,19	5,486	3,46	4,88
Табличное значение t- критерия Стъюдента ( tтабл. )	2,18	2,76	2,17	2,179	2,179	2,179
Критерий Дарбина – Уотсона (D W )	1,82	1,31	1,86	1,73	1,89	1,73

Основные этапы эволюционного поиска представляют собой классический вариант и включают:

• 1)    конструирование начальной популяции (вводится точка отсчета поколений t =0, вычисляется приспособленность каждой хромосомы в популяции, а затем средняя приспособленность всей популяции);

• 2)    установление популяции t = t +1 (производится выбор хромосом-родителей для реализации оператора кроссинговера, который выполняется в соответствии с заданными параметрами);

• 3)    формирование генотипа потомков (в соответствии с заданными вероятностями выполняется оператор скрещивания, после чего производится оценка потомков с сохранением части как членов новой популяции);

• 4)    применение оператора мутации с заданными вероятностями к полученным хромосомам;

• 5)    применение оператора редукции для исключения лишних хромосом из популяции согласно условию неизменности размера популяции. Текущая популяция обновляется заменой отобранных хромосом на потомков;

• 6)    определение функции приспособленности и пересчет средней приспособленности всей полученной популяции;

• 7)    проверка на достижение останова алгоритма.

Моделирование «эволюционного процесса» прекращается в случаях выполнения условий:

• –    нахождения глобального (субоптимального решения);

• –    невозможности достижения сходимости алгоритма.

Процесс поиска включает 3 основных этапа, повторяемых в цикле:

• –    эволюция – сдвиг варианта в направлении ожидаемого оптимума;

• –    отсеивание «неудачных» вариантов;

• –    скрещивание «удачных» вариантов: порождение вариантов – «потомков», сочетающих удачные значения параметров «родителей».

Архитектура эволюционного поиска на основе миграции приведена на рисунке.

Блоки ГА 1111 , ГА 1112 , ГА 111 , ГА 112 , ГА 11 , ГА 12 выступают как простые генетические алгоритмы, где выполняются различные операторы репродукции. В блоки миграции ( ГА 1 , ГА 11 , ГА 111 ) каждый раз отправляются лучшие представители популяций.

Основные положения работы генетического алгоритма включают конструирование начальной популяции случайным образом в рамках интервалов заданных значений, селекцию на основе методов пропорционального и турнирного отбора, генерацию каждого нового поколения при помощи операторов кроссинговера и мутации, а также условие неизменного размера популяции.

На этапе создания начальной популяции используются статистические данные в кодированном виде, которые представляют собой возможные значения заданного диапазона. Для данного генетического поиска выбрана кодировка значений факторов в виде десятичных чисел. Количество ДНК в каждом генетическом алгоритме зависит от количества влияющих факторов и колеблется от двух до четырех ДНК в хромосоме. Каждое ДНК состоит из 4-6 генов и определяет значение одного фактора, закодированное символами от 0000 либо 000000 (минимальное значение) до 9999 либо 999999 (максимальное значение).

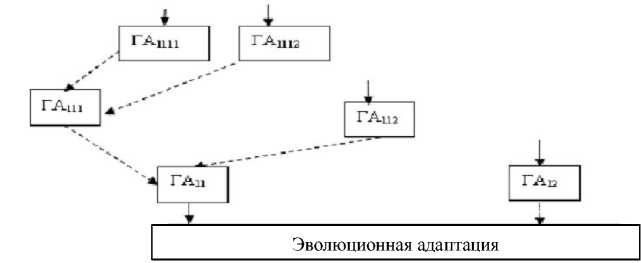
Рис. Архитектура генетического поиска на основе миграции

Хромосомы генетических алгоритмов более высокого уровня включают в себя хромосомы более низких, это позволяет не терять реальные значения факторов при переходе данных в следующий генетический алгоритм.

При разработке прогноза показателей научного потенциала с использованием генетического алгоритма возникла проблема, связанная с малым размером начальной популяции. Для ее устранения использовалась процедура увеличения популяции, а также самоадаптация алгоритма при выборе операторов. Была выбрана начальная популяция, составляющая 1000 особей, сформированная двумя способами случайным отбором хромосом в диапазоне допустимых значений и комбинацией значений (минимальные, средние, максимальные, %, % значения показателей).

Генерация нового поколения осуществлялась на основе применения операторов селекция, скрещивания, мутации. Для разработки прогноза показателей научного потенциала были отобраны два метода селекции - турнирный и пропорциональный. Метод селекции отбирался случайным образом из условия вероятности выбора метода пропорциональной селекции - 50%, метода турнирной селекции - 50%. Технология турнирной селекции включает выбор хромосом в размере от 2 до (число хромосом)/2+2, сортировку выбранных хромосом по значениям функции приспособленности и выбор двух хромосом с наилучшими значениями функции. При турнирной селекции отбор особи с наилучшей приспособленностью в популяции осуществлялся при помощи детерминированного способа выбора с вероятностью равной единице. Вероятность выбора каждой группы P(Bx ) можно рассчитать как отношение числа турниров Mx, в которых побеждает группа Bx, к числу числа всех возможных турниров M :

p ( ^B x ) = MT x M

M x

C

T

N

При пропорциональной селекции происходит сложение значений функции приспособленности и выбор случайным образом двух значений из заданного диапазона. Число вхождений особи непосредственно пропорционально приспособленности особи, т.е. значению функции приспособ- ленности.

Скрещивание хромосом осуществляется рядом операторов: одноточечный, двухточечный и арифметический кроссоверы. Процентное соотношение кроссоверов ряда задается в виде исход -ной информации алгоритма, например, 30% хромосом участвуют в одноточечном скрещивании, 30% - в двухточечном скрещивании и 40% - в арифметическом. В первом и втором случаях случайным образом выбираются точки разрыва, и происходит скрещивание с сохранением новых хромосом в новом поколении. При арифметическом скрещивании обмен генами осуществляется посредством вычисления значений генов потомков на основе значений генов родителей по форму- ле:

H i k = w ^х c ik + ^{(1 -} w ) ^х c 2 к ;

H 2 к = w ^х c 2 к ^{+ (1} — w ) ^х c i к , где k - номер гена; c ₁ , c ₂ - первая и вторая родительские хромосомы; H ₁ , H ₂ - первый и второй потомки; w - коэффициент, значения которого лежат в интервале [0;1].

На следующей стадии пара хромосом, созданная оператором скрещивания, заносится в новое поколение. На стадии мутации происходит случайный отбор изменяемого гена. В работе реализовано два вида мутации - случайная (ненаправленная) и направленная. В первом случайным образом происходит выбор изменяемого гена. На его место случайным образом выбирается новое значение. Во втором выбирается ген с наименьшим (или наибольшим в случае минимизации фактора) значением и увеличивается (уменьшается) на определенное значение. Отличие от классических генетических алгоритмов состоит в сохранении вещественных векторов решений. Вторым отличием является порядок реализации основных генетических операторов, который состоит из стадии «воспроизводства» новых решений, включающей в себя три элемента: выбор элементов для скрещивания, генерация новых решений с помощью ряда операторов «кроссовер», локальные изменения большого числа решений с помощью оператора направленной мутации. После этого осуществляется процедура построения совокупности решений для следующей итерации («поколения») из всего множества доступных к тому моменту решений. Представленный алгоритм относится к так называемым «поколенческим» (термин ДеЯнга) эволюционным алгоритмам, в которых эволюция идет от одной итерации к другой, допуская появление к>>1 новых решений, накапливаемых в репродукционном множестве, прежде чем включится процесс отбора, отбрасывающий лишние к решений.

Для выбора параметров генетического алгоритма и конкретных генетических операторов в алгоритм встроено несколько различных операторов выборки (элитная, случайная, рулеточная), кроссинговера (одноточечный, двухточечный, унифицированный) и мутации (случайная одноэлементная, абсолютная). Для каждого оператора установлены равные вероятности применения. На каждом цикле алгоритма выбирается один из операторов каждой группы (выбор, кроссинговер, мутация) соответственно вероятностному распределению. Причем в полученной при помощи этих операторов особи отмечается, какими именно операторами она была получена. Поскольку новое распределение вероятностей вычисляется исходя из информации, содержащейся в популяции, то генетический алгоритм получает механизм динамической самоадаптации.

Такой подход дает еще одно преимущество, а именно неиспользование генератора случайных чисел, так как алгоритм динамически изменяет характер распределения.

Результаты

Для каждого генетического алгоритма была найдена собственная функция приспособленности на основе статической обработки исходных данных.

Для оценки возможности применения методологии эволюционных вычислений в задачах прогнозирования научно-инновационного развития республики проведены расчеты показателей научного потенциала республики. Прогноз осуществлялся исходя из референтных точек показателей, заданных на определенных условиях.

На основе использования критерия «исчерпывание числа поколений, отпущенных на эволюцию» был осуществлен расчет 40 поколений. В результате прогнозное значение обобщающего показателя имело диапазон от 0,79 до 1,178. Затем производился итеративный отбор возможных вариантов получения оптимального прогнозного значения обобщающего показателя. Итеративный поиск позволил получить 22 решения с небольшими отклонениями по одному–двум параметрам. Из данной совокупности было найдено 8 субоптимальных решений, каждый из которых имеет значения показателей, соответствующих заданному диапазону. Поскольку в задачи прогнозирования было заложено условие снижения уровня финансирования за счет бюджетных средств, то наиболее оптимальным вариантом может быть вариант, представленный в таблице 2.

Оптимальные значения прогнозных показателей

Таблица 2

	Результирующий фактор	Диапазон значений	Оптимальное решение генетического поиска
ГА 1	Доля научно-исследовательских работ в ВРП	0,264 : 1,2	0,799
ГА 11	Численность персонала, занятого НИР, на 10000 занятых в экономике	25 : 70	44
Г 111	Доля исследователей в общей численности, занятых НИР	0,7 : 0,9	0,877
ГА 112	Доля исследователей высшей квалификации	0,3 : 1	0,856
ГА 1111	Доля исследователей в технических науках	0,04 : 0,3	0,259
ГА 1121	Доля исследователей в сельскохозяйственных науках	0,2 : 0,45	0,344

Полученные результаты позволяют сделать вывод о возможности использования генетического алгоритма для прогнозирования показателей развития сложных систем.