Прогнозирование поступлений налога на прибыль в консолидированный бюджет региона
Автор: Чимитдоржиева Е.Ц.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Экономические науки
Статья в выпуске: 5-4 (32), 2019 года.
Бесплатный доступ
Прогнозирование налоговых доходов является обязательным этапом бюджетного процесса. В статье для построения прогноза поступлений налога на прибыль предлагается использовать модель авторегрессии и проинтегрированного скользящего среднего. Применение данного подхода к прогнозированию дает достаточно хороший результат и его можно использовать на практике.
Модель авторегрессиии проинтегрированного скользящего среднего, налог на прибыль, прогноз
Короткий адрес: https://sciup.org/170186353
IDR: 170186353 | DOI: 10.24411/2500-1000-2019-11036
Текст научной статьи Прогнозирование поступлений налога на прибыль в консолидированный бюджет региона
Налог на прибыль является одним из основных бюджетообразующих налогов для многих регионов страны, в том числе для Республики Бурятия. Удельныйвес на- лога в общей сумме налоговых доходов консолидированного бюджета региона с 2013 г. по 2018 г. менялся с 15,13% до 28,95% (рис. 1).
удельный вес НП
Рис. 1. Удельный вес налога на прибыль в общей сумме налоговых доходов с 2013 г. по 2018 г.
Следовательно, прогнозирование данного вида дохода для консолидированного бюджета региона является важной задачей. Несмотря на увеличение срока планирования бюджета (до трех лет), краткосрочное прогнозирование по-прежнему остается актуальным, так как дает возможность оценить наполняемость бюджета в течение года, позволяет учесть сезонные колебания в поступлениях налоговых доходов.
Визуальный анализ динамики поступления налога на прибыль не дает возможности определить наличие тренда и сезон- ных колебаний (рис. 2). Поступления данного вида налога имеют высокую волатильность максимальное значение за весь период наблюдений достигнуто в марте 2015 г. (2411562 тыс. руб.), минимальное значение – в июне 2014 г. (-132092 тыс. руб.). Среднее квадратическое отклонение ряда динамики, рассчитанное по налогу на прибыль, составило 485288 тыс. руб. Для сравнения аналогичный показатель, рассчитанный по налогу на доходы физических лиц составил 293916 тыс. руб., что 1,65 раза меньше [1].
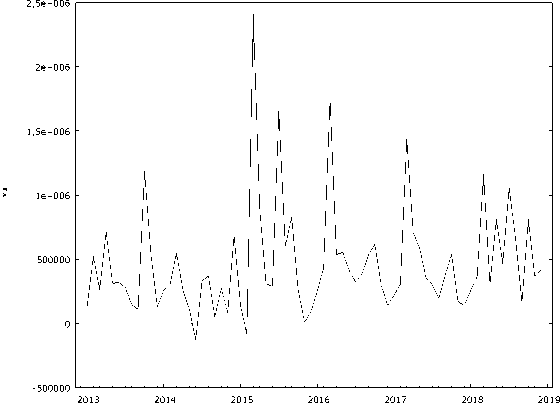
Рис. 2. Поступления налога на прибыль в консолидированный бюджет Республики Бурятия с 2013 г. по 2018 г. по месяцам
Для прогнозирования поступлений данного вида налоговых доходов нами была использована методология Бокса– Дженкинса, которая строится на предположении, что временной ряд является стационарным [2]. Для проверки имеющегося временного ряда на стационарность был использован расширенный тест Дики– Фуллера. Тест с константой показал, что ряд не стационарен. При этом расширенный тест Дики–Фуллера с константой для первых разностей показал р-значение на уровне 1,159Е-7, что свидетельствует о стационарности процесса первых разностей.
Следующим этапом формирования эконометрической модели является определение ее порядка. Для этого нужно рассмотреть автокорреляционную функцию и частную автокорреляционную функцию исходных данных. График автокорреляционной функции и частной автокорреляционной функции не дал возможности определить порядок модели (рис. 3). Обе функции ведут себя практически одинаково, для них является характерным выброс на 12 лаге.
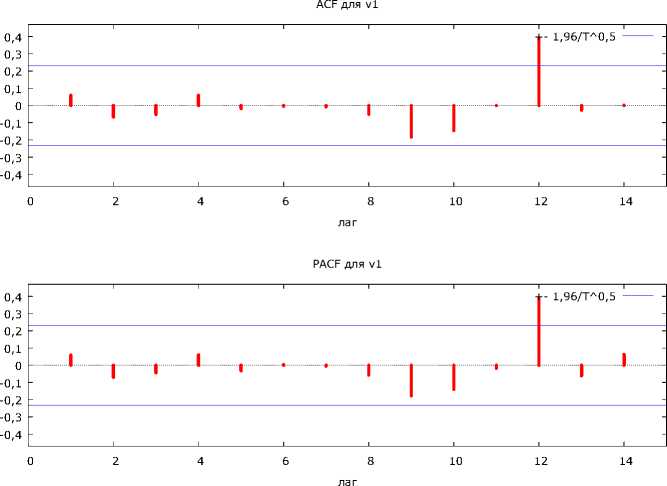
Рис. 3. Автокорреляционная функция для исходной переменной
Для получения адекватной информации о порядке модели авторегрессии и проинтегрированного скользящего среднего возникла необходимость в построении графика автокорреляционной функции и частной автокорреляционной функции для первых разностей временного ряда. Автокорреляционная функция имеет выбросы на 1, 11, 12, 13 лагах, частная автокорреляционная функция постепенно убывает.
Для подобных автокорреляционных функций характерен процесс скользящего среднего первого порядка. Автокорреляции значимые на 11, 12, 13 лагах указывают на сезонность поступлений налога на прибыль.
Таким образом, нами были получена эконометрическая модель поступлений налога на доходы физических лиц (табл. 1).
Таблица 1. Характеристика модели авторегрессии и проинтегрированного скользящего среднего (0,1,1) (0,1,1)
|
Параметр |
Значение параметра |
Стандартная ошибка |
z |
Значимость |
|
p (1) |
-0,920571 |
0,116168 |
-7,924 |
<0,0001 |
|
Ps (1) |
-0,999998 |
0,315710 |
-3,167 |
0,0015 |
Параметры модели являются значимыми. Критерий Акаике принимает минимальное значение (1706,781) по сравнению с аналогичными показателями, которые были рассчитаны по другим «рабочим» моделями. Критерий Шварца составляет 1713,014, что также является наименьшим значением.
Анализ остатков показал, что их автокорреляционная функция и частная автокорреляционная функция приближаются к характеристикам белого шума. Проверка статистической гипотезы Льюинга–Бокса дает возможность говорить об отсутствии автокорреляции до 12 порядка.
Остатки эконометрической модели имеют нормальное распределение, проверка гипотезы о нормальном распределении осуществлялась по критерию χ2.
Анализ качества построенной модели указывает на возможность ее использования для построения прогноза. Нами был получен прогноз на 2019 г. по месяцам, доверительные интервалы построены исходя из надежности 95% (рис. 4).
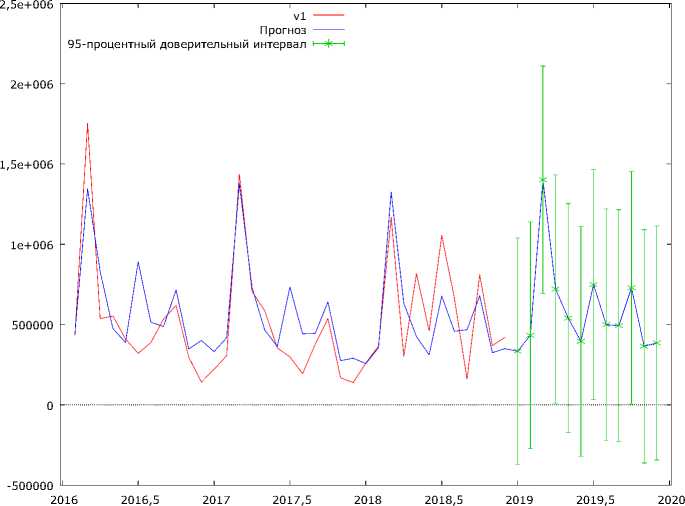
Рис. 4. Прогноз поступлений налога на прибыль в 2019 г. по месяцам
Таким образом, применение методологии Бокса–Дженкинса к прогнозированию поступлений налога на прибыль дало возможность достаточно точно оценить будущие значения. Одним из преимуществ данного подхода, на наш взгляд, является четкая алгоритмизация процесса построения модели, по сравнению с другими, эвристическими.
Список литературы Прогнозирование поступлений налога на прибыль в консолидированный бюджет региона
- Чимитдоржиева Е.Ц. Прогнозирование поступлений налога на доходы физических лиц в консолидированный бюджет региона // Актуальные вопросы права, экономики и управления: сб. статей XIX международной научно-практической конференции, состоявшейся 5 мая 2019 г. в г. Пенза. - Пенза, 2019. - С. 127-130.
- Бокс Дж., Дженкинс Г. Анализ временные рядов, прогноз и управление [Текст]: В 2 т. Т. 1 / Дж. Бокс, Г. Дженкинс; [пер. с англ.]. - М.: Мир, 1974. - 405 с.


