Прогнозирование потерь электроэнергии в сетях низкого напряжения на основе регрессионного анализа

В состав энергосистемы входит несколько тысяч линий электропередач напряжением до 1000 В. Такие сети являются важнейшим звеном в системе электроснабжения промышленных предприятий. Вследствие их большой разветвленности и протяженности линии низкого напряжения характеризуются довольно высокими потерями электроэнергии. Поэтому при наблюдаемом росте стоимости электрической энергии актуально повышение точности расчетов потерь в этих сетях.

Для более точного определения потерь электроэнергии представляется целесообразным применение специализированных моделей, параметры которых легко находятся отдельно для каждой конкретной цеховой сети. При составлении таких моделей все линии радиальной цеховой сети заменяются одной эквивалентной линией.

Эквивалентные параметры моделей вычисляются на основе вероятностно-статистического подхода и учитывают обобщенные физические характеристики сетей. Таким образом, для определения эквивалентного сопротивления можно получить упрощенные выражения, обеспечивающие необходимую точность и позволяющие сократить объем требуемой исходной информации.

В такой ситуации целесообразно воспользоваться методами регрессионного анализа и теории планирования эксперимента, на основе которых в ряде случаев можно получить вероятностностатистические модели, реализующие зависимость эквивалентного сопротивления сети от ее обобщенных параметров.

Определение эквивалентного сопротивления и потерь электроэнергии в радиальных сетях

Для решения задачи интерполяции [1], в которой функцией цели выступают потери мощности и эквивалентное сопротивление цеховой сети, в качестве факториальных признаков нами выбраны основные обобщенные параметры радиальной цеховой сети:

x1 – отношение суммарной длины линий цеховой сети к количеству линий, т. е. средняя длина линий lср

2 ” = 1 к

где l_i – длина i -й линии цеховой сети, м; n – количество линий;

x ₂ – величина, равная количеству линий n ;

x ₃ – величина, равная эквивалентному удельному сопротивлению линий сети r_{э 20} при 20 ºС;

n l

Г э20 = 31,3^^- •

2"Ы Sl где Si – сечение i-й линии, мм²; 31,3 Si – сопротивление 1 м алюминиевой линии сечением Si при 20 ºС, Ом/м; в случае, когда часть линий сети выполнена проводами или кабелями с медными жилами, используется величина 18,5 Si ;

x4 – квадрат среднеквадратичного коэффициента загрузки линий сети kз2

2 n = k 2

n

где кзi = IjTномi - коэффициент загрузки i-й линии; I – ток в i-й линии, А; I – номинальный i                                    номi ток в линии Si -го сечения, А.

x 5 - температура окружающей среды 9₀, °C.

С параметром фактора x ₃ имеет прямую связь величина сопротивления коммутационных аппаратов, принятых к установке на линии данного сечения. Определив по значению x ₃ номинальный ток линии, можно вычислить сопротивление аппарата, используя аналитические зависимости коммутационных аппаратов от номинального тока [2]. На основании статистических данных считаем, что в среднем на линии цеховой сети установлены 2 коммутационных аппарата.

Первоначальные диапазоны варьирования факторов охватывают сети со средней площадью цехов, средняя длина линий сети заключена в пределах от 10 до 100 м при количестве линий от 10 до 20; номинальная мощность цеховых трансформаторов – 250–1600 кВ·А, чему соответствует предел изменения средней величины сечения линий от 16 до 120 мм² (рис. 1). При этом допустимый суммарный ток линий – 380–2400 А (при полной их загрузке). Диапазон изменения коэффициента загрузки линий находится в пределах от 0,3 (что соответствует малонагруженной сети) до 1 (что соответствует полностью загруженной сети). Для температуры окружающей среды приняты пределы, соответствующие крайним значениям температуры помещений цехов +5…+35 °С.

Первоначальные границы изменения факторов представлены в таблице, где

X -X- ■ д x =  i max i2

Первоначальные границы изменения факторов

Фактор	i min	i ср	X-i max	Д Х ,
x 1 ^ l ср , м	10	55	100	45
x 2 ^ n	10	15	20	5
x 3 ^ гэ20 , Ом/м	1,956	1,108	0,261	0,848
x 4 ^ k з	0,09	0,545	1,00	0,455
x 5 ^ 0 0 , °C	5	20	35	15

Таким образом, эквивалентное сопротивление радиальных сетей вычисляем по выражению

R = { r₃ 20 • l [ 1 + 0,004 ( 0 ж — 20 ) ] + £ r } • n, (1)

9ж = кз2 (80-00 ) + 00,(2)

где l – длина проводника, м; θ _ж – температура жилы кабеля, 80 – допустимая температура нагрева жилы кабеля; ^ r k - сумма сопротивлений автоматических выключателей, установленных на линии.

Для многофакторной корреляционной модели рассматривается следующая форма связи результативного показателя с факториальными: Y = b ₀ + b 1 x 1 + b ₂ x ₂ + b 3 x 3 + b ₄ x ₄ + b ₅ x ₅ + b ₁₂ x 1 x ₂ + + b 13 x 1 x ₃ + b j ₄ x 1 x ₄ + b 1 ₅ x 1 x ₅ + b ₂₃ x ₂ x 3 + b ₂₄ x ₂ x ₄ +

^{+ b} 25 ^x 2 ^x 5 ^{+ b} 34 ^x 3 ^x 4 ^{+ b} 35 ^x 3 ^x 5 ^{+ b} 45 ^x 4 ^x 5^{.               (3)}

Для разработки математической модели потерь электроэнергии воспользуемся дробным факторным экспериментом (ДФЭ) типа 25-1 с генери-

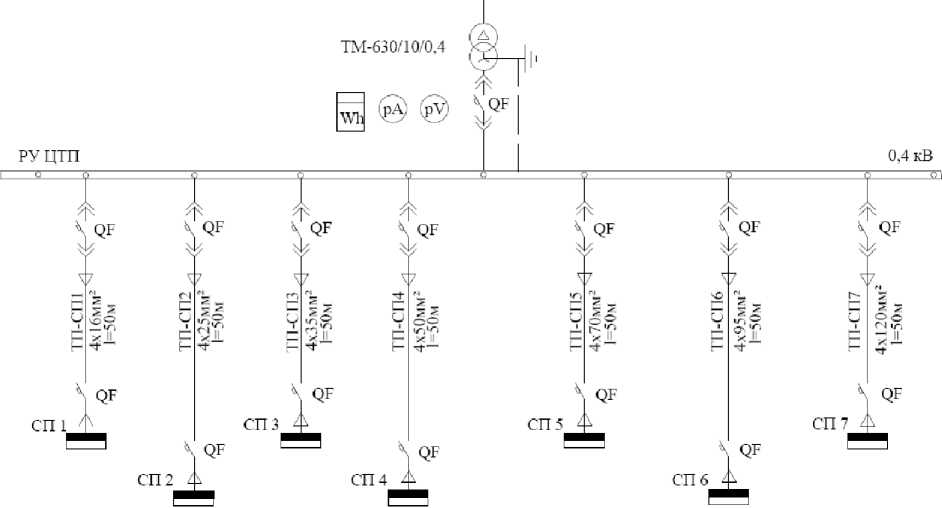
Рис. 1. Радиальная схема цеховой электрической сети

рующим соотношением х 5 = х 1 · х 2 · х 3 · х 4 [3]. Этот план позволяет раздельно оценить линейные эффекты и парные взаимодействия. Тройными и выше взаимодействиями пренебрегаем. Значения функции цели при различных диапазонах варьирования факторов вычисляем, используя выражение (1)–(2) применительно к радиальной сети.

В уравнении (3) коэффициенты b0… b45– ис- комые коэффициенты уравнения регрессии, вычисляемые по методу наименьших квадратов [4]:

b —

N

/ < u = i y u x lU  ₇

N ; ij

E N

, У и ■ x ■ x U1* u lu ju

N где l, j - номера факторов; xt,Xj - кодированные значения факторов (+1 или –1); yu – значение выходной величины (потерь мощности и эквивалентного сопротивления); u – номер опыта; N – число опытов (в нашем случае N = 16).

После вычисления значений коэффициентов bi и bij полином (3) примет вид регрессионных зависимостей Rэ – эквивалентного сопротивления цеховой сети и ∆Р – потерь мощности

R э — 5,4 + 4,2 x 1 - 1,7 x ₂ - 3,9 x ₃ + 0,53 x ₄ + + 0,23 x ₅ - 1,3 xx ₂ - 3,19 xx ₃ + 0,44 xx ₄ + + 0,22 x 1 x ₅ + 1,22 x ₂ x ₃ - 0,24 x ₂ x ₄ - 0,35 x ₂ x ₅ -

-0,4 x ₃ x ₄ - 0,23 x ₃ x ₅ + 0,95 x ₄ x ₅ ;               (4)

A P — 48 + 36,4 x 1 - 16 x ₂ - 11,2 x ₃ + 41,5 x ₄ +

3,34 x ₅ - 12 x 1 x ₂ - 11 x 1 x ₃ + 31,4 x 1 x ₄ - 11,05 x 1 x ₅ + 3,62 x ₂ x ₃ - 13,9 x ₂ x ₄ - 9,6 x ₂ x ₅ - 9,8 x ₃ x ₄ -

-10,5 x ₃ x ₅ + 3,53 x ₄ x ₅ .

значены значения, предсказанные аппроксимирующим выражением) использовались в качестве основы для формальной процедуры исключения незначимых коэффициентов, выбрасывание которых лишь весьма слабо влияло на величину указанных разностей.

После исключения незначимых коэффициентов b ₁₅ — 0,22; b ₂₅ —- 0,35; b ₃₅ —- 0,23 в полиноме (4) и b ₁₅ —- 11,05; b ₂₅ — -9,6; b ₄₅ — 3,53 в полиноме (5) они примут следующий вид: R э — 5,4 + 4,2 x 1 - 1,7 x ₂ - 3,9 x ₃ + 0,53 x ₄ + + 0,23 x ₅ - 1,3 x 1 x ₂ - 3,19 x 1 x ₃ + 0,44 x 1 x ₄ + + 1,22 x ₂ x ₃ - 0,24 x ₂ x ₄ - 0,4 x ₃ x ₄ + 0,95 x ₄ x ₅ ;       (6)

A P — 48 + 36,4 x 1 - 16 x ₂ - 11,2 x ₃ + 41,5 x ₄ + + 3,34 x ₅ - 12 x 1 x ₂ - 11 x 1 x ₃ + 31,4 x 1 x ₄ + + 3,62 x ₂ x ₃ - 13,9 x ₂ x ₄ - 9,8 x ₃ x ₄ - 10,5 x ₃ x ₅ .        ⁽⁷⁾

По полиноминальной модели (6) строятся номограммы для определения эквивалентного сопротивления. На рис. 2–3 представлены некоторые из них. Номограммы построены для линий с различным сечением, различных значений средней длины линий и загрузки.

Для определения эквивалентного сопротивления по оси абсцисс требуется отложить значение суммарной величины сечения линий ( s∙n ) и по кривой соответствующего коэффициента загрузки линий на оси ординат найти искомое значение.

Получив значения коэффициентов для кодированных факторов, можно перейти к записи полиномов в натуральных величинах. Для преобразования воспользуемся выражением

При исследовании полученного уравнения необходимо отбросить члены с незначимыми коэффициентами. Поэтому в рассматриваемой задаче проводились расчеты в ряде дополнительных точек факторного пространства и полученные в

~ xl—

xi

—

x i 0

A x_l

них

разности R э - R | и |a P - A P (значком

л обо-

где 5 ci - кодированное значение фактора; x _l - действительное значение фактора; x ₀ – нулевой уровень фактора; A x_l - шаг варьирования фактора.

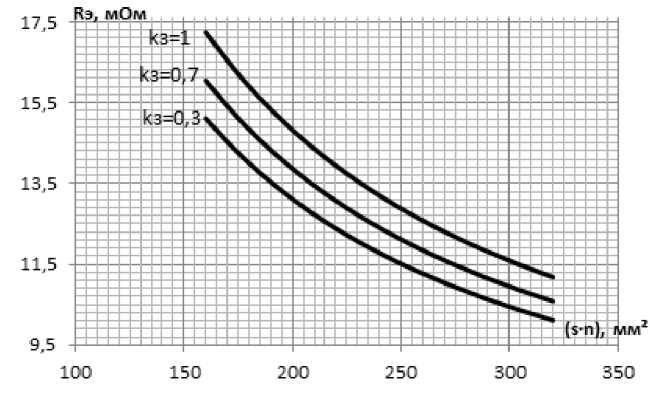
Рис. 2. Номограммы эквивалентного сопротивления для линий сечением 16 мм², средней длины линий 50 м и температуры окружающей среды 20 ºС

После подстановки значений кодированных факторов в уравнение регрессии и преобразований получим полиномы в натуральном масштабе, которые будут иметь вид:

R э = 2,5 + 1,3 - 1 ср - 0,01 - n + 6,5 - 10—⁴ - 5 + + 0,16 - k 3 + 0, 002 0 q — 6,5 - 10 -^ - 1 ср - n + + 1,7 - 10 - 1 ср - 5 + 0,003 - 1 ср - k 3 — -4,03 - 10 - ⁵ - n - 5 — 0,007 - n - k ₃ ² — -1,5 - 10 - ⁴ - 5 - k ₃ ² — 1,9 - 10 - ³ - k ₃ ² -O q ;

AP = 5,47 — 0,1-1ф + 0,3- n + 0,1- 5 +15,9 - k3 — -0,9 - Oq — 0,01-1ф - n + 0,002 -1ф - 5 + 0,3- 1ср - k2 — -0,01- n - 5 — 1,5- n - k3 + 0,3- 5 - k3 — 0,003 - 5 - Oq, где входящие в полиномы величины имеют следующие ра3мерности: Rэ - [мОм]; ДР - [кВт];

Определение эквивалентного сопротивления и потерь электроэнергии в магистральных сетях

Линии магистральных сетей (рис. 4), как правило, представляют собой шинопроводы с распределенной электрической нагрузкой. В качестве параметров, определяющих потери электроэнергии и эквивалентное сопротивление, выступают такие величины, как длина шинопровода, количество приемников, подключенных к шинопроводу и т. д.

Потери мощности в магистральных сетях определяются по выражению

A P ш = 3 I э² R . ,                               (8)

где R _эш – эквивалентное сопротивление шинопровода, вычисляемое из уравнения

1 ср - [м]; ^ э20 - [мОм/м]; O q - [ ° С].

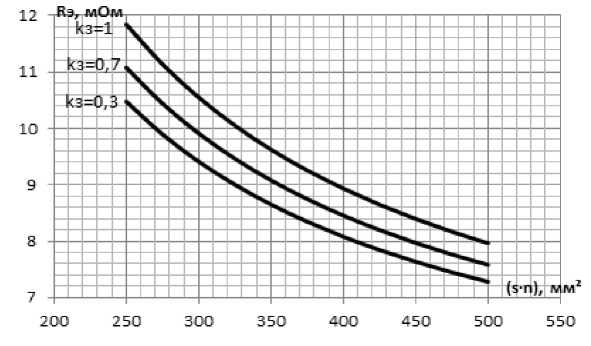
Рис. 3. Номограммы эквивалентного сопротивления для линий сечением 25 мм², средней длины линий 50 м и температуры окружающей среды 20 ºС

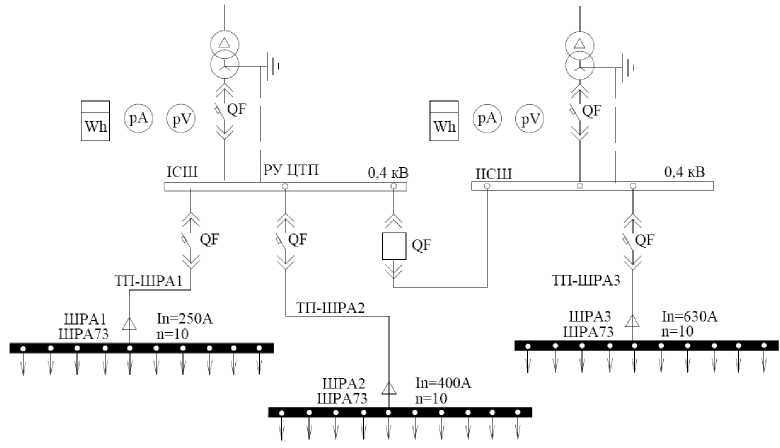
Рис. 4. Магистральная схема цеховой электрической сети

R эш

Гэ20 ' l' С   1 V   В

I       1 II        1 I

6 1 1 + II 2 + I

I   n Д

X

x[ 1 + a ( 0-0 0 ) ] + k . (9)

Здесь r ₂₀ – сопротивление 1 м шинопровода при 20 °С, мОм; l – длина шинопровода, м; n – количество приемников, присоединенных к шинопроводу; r _п – сопротивление провода ответвления от шинопровода, мОм; I _э – эффективный ток, А; r_k – сопротивление коммутационного аппарата ответвления, мОм; α – температурный коэффициент увеличения сопротивления, 1/°С; 0 - температура шинопровода, °С; 0 0 - температура окружающей среды, °С.

Регрессионные модели для определения эквивалентного сопротивления и потерь электроэнергии в шинопроводе определяются согласно алгоритму, приведенному выше для радиальных сетей. По полиноминальной модели для магистральной сети были построены номограммы. Некоторые из них представлены на рис. 5–6. Эквивалентное со- противление является функцией значения (s ■ n), где s – сечение шинопровода, n – количество присоединенных приемников.

Определение эквивалентного сопротивления смешанных схем цеховых сетей

Для электроснабжения цеховых потребителей очень редко применяются радиальные или магистральные схемы в чистом виде. Наибольшее распространение обычно находят так называемые смешанные схемы электрических сетей, сочетающие в себе элементы радиальных и магистральных схем.

Для определения эквивалентного сопротивления смешанных схем требуется выделить радиальные и магистральные участки сети. Затем при помощи соответствующих номограмм найти эквивалентные сопротивления выделенных радиальных и магистральных участков - R _э(_р) и R э ( м ) . Эквивалентное сопротивление смешанной схемы сети при параллельном соединении радиального и магистрального участков определиться как

R э(р) R э(м)

R ^э(™)     п , п .

^R э(р) ^{+ R} э(м)

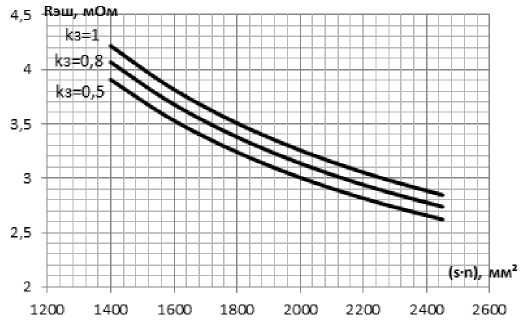
Рис. 5. Номограммы эквивалентного сопротивления шинопровода

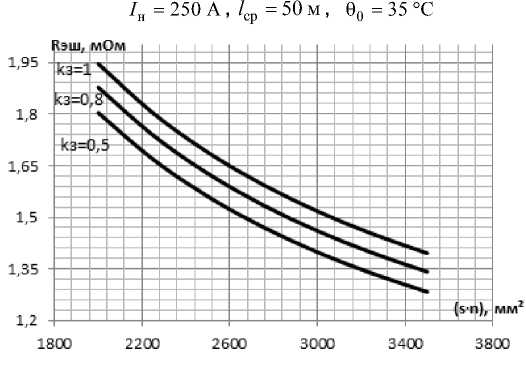
Рис. 6. Номограммы эквивалентного сопротивления шинопровода

I _н = 400 А , l ср = 50 м , 0 0 = 35 ° С

Заключение

Таким образом, при определении и прогнозировании потерь электроэнергии целесообразно составлять специализированные модели, параметры которых следует определять в функции обобщенных параметров сети, используя регрессионный анализ. Вероятностно-статистические модели для нахождения эквивалентного сопротивления Rэ и потерь мощности цеховых сетей ΔP позволяют учесть такие параметры как длина, количество, сечение линий сети, температура окружающей среды, число коммутационных аппаратов на линии и количество электроприемников, присоединенных к шинопроводу. Данные модели позволяют достаточно просто учитывать динамику измене- ния электрических сетей, поэтому пригодны для многократного использования.