Прогнозирование ресурса железобетонных монолитных плит перекрытия

В наши дни основным конструкционным материалом для строительных целей в Российской Федерации является железобетон. Железобетон – это композиционный строительный материал, который включает в себя бетон и сталь. Изделия из железобетона, имеющие ряд преимуществ по сравнению с другими материалами, с успехом эксплуатируются в строительстве.

На начальном этапе проектирования все здания и сооружения должны отвечать нормативным требованиям с учетом влияния действия нагрузок и агрессивных сред. Несоблюдение проектных рекомендаций ведет к преждевременному износу конструкций и их разрушению. Возрастающее число крупных и мелких аварий, выход объектов из строя ведет к потерям финансовых ресурсов. Только в России эти финансовые издержки оцениваются примерно в 20-25 миллиардов рублей ежегодно. Задача обеспечения долговечности и коррозионной стойкости железобетонных изделий и конструкций является актуальной. Для решения поставленной задачи необходимо разработать методику оценки и прогнозирования ресурса железобетонной конструкции с учетом реальных условий эксплуатации при совместном действии силовых и химически активных сред.

Многими отечественными и зарубежными учеными были описаны процессы коррозии, выявлены и описаны основные характеристики процесса разрушения строительных конструкций, предложены расчетные методы оценки долговечности. Н. С. Стрелецким был предложен универсальный подход по нахождению оптимального срока службы, который должен определяться по минимуму эксплуатационных расходов [1]. В. В. Болотиным, А. Р. Ржаницыным, В. М. Бондаренко, Е. А. Гузеевым, В. И. Соломатовым, В. П. Селяевым, А. И. Попеско и др. были предложены современные методы оценки расчета надежности и долговечности строительных конструкций, основанные на принципах теории вероятности, математической статистики и теории случайных процессов [2-4].

В данной работе рассматривается метод, основанный на применении деградационных функций для оценки и прогнозирования ресурса железобетонных конструкций.

Деградация - это процесс ухудшения характеристик, качества строительных материалов и конструкций при воздействии силовых факторов, химических веществ, живых организмов, агрессивных сред. Для оценки долговечности строительных изделий предложено вместо коэффициентов условий работы применять функции деградации, выражающие изменение во времени несущей способности или жесткости поперечного сечения элемента [4]. Каждому механизму деградации соответствуют определенные модели деградации. Общий вид деградационной функции можно представить выражением [5]:

D =^ = f(t,T, (1)

#w

Метод деградационных функций позволяет комплексно оценивать действие агрессивных сред на элемент строительной конструкции. Вместе с этим появляется возможность учитывать интенсивность деструкции материала, вид напряженного состояния, размеры образца и их изменение под действием среды, распределение прочностных свойств по площади поперечного сечения.

Определение ресурса рассмотрим на примере расчета железобетонной плиты. Для описания процесса взаимодействия материала с агрессивной средой примем модель деградации по диффузионному типу (рис. 1). Диффузионные модели деградации применимы в тех случаях, когда скорости переноса и химического взаимодействия реакционноспособных компонентов материала и среды сопоставимы.

Основными параметрами модели являются: глубинный показатель a(t), коэффициент химического сопротивления к_хс. Первый параметр а. характеризует скорость продвижения фронта разрушения материала с поверхности вглубь образца. Второй параметр к_хс является оценкой скорости изменения твердости или прочности внешних слоев материала, контактирующих с агрессивной средой.

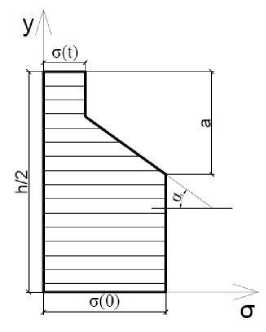
Рис. 1. Модель деградации.

Глубинный показатель предложено определять по сорбционным характеристикам т₀

и t05. На рисунке 2 приведены экспериментальные данные по изменению массы образцов, экспонированных в воде. Кривые сорбции хорошо описываются уравнением Ленгмюра:

т =

m₀t t+t o,5

Линеаризация данных по сорбции в осях 1/т - 1/t дает возможность определить т0 и t0,5. На рисунке 3 показано, что экспериментальные данные изменения массы образцов, экспонированных в воде, хорошо описываются линейной зависимостью. По графикам (рис. 2 и 3) были получены сорбционные характеристики т0 и t0,5 (см. табл. 1). Коэффициент диффузии и глубинный показатель предложено [6; 7; 8] определять путем решений уравнений Ленгмюра и Фика по формулам:

R 2

°=0,2    ;                                   (3)

а = 0,1VDt .                                 (4)

Таблица 1

Константы сорбции т₀ и t₀ , ₅ для цементных образцов, экспонированных в H 2 O

№ п/п	Среда	т 0 гр.	t0,5 сут.	^(t)/^(0)
				0	1	2
1	H 2 O	0,09	191	1	0,802	0,592

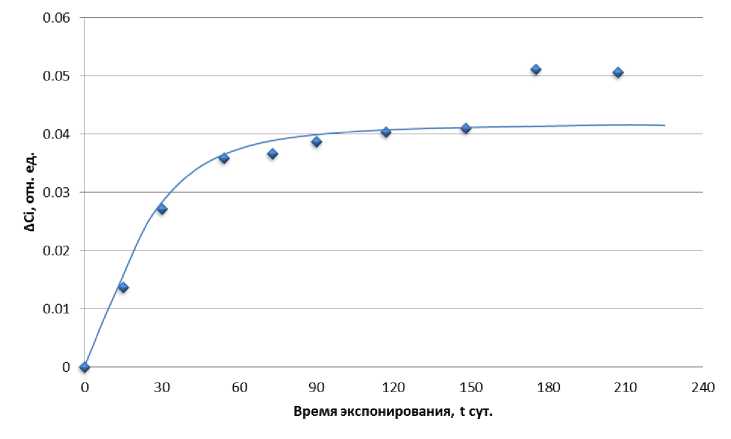
Рис. 2. Приращение по массе цементных композитов, выдержанных в H 2 O.

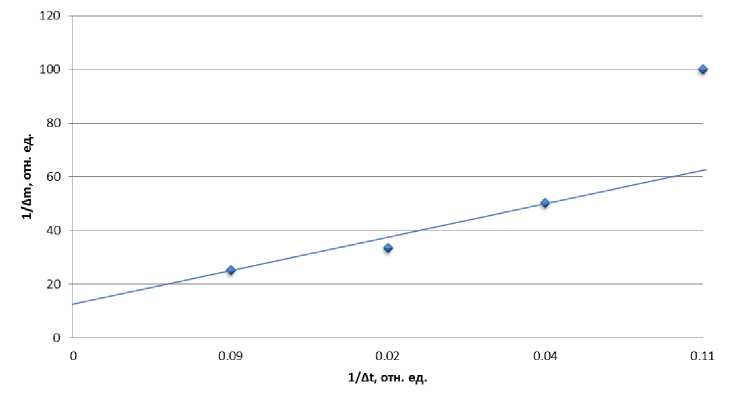
Рис. 3. Изменение массы цементных композитов, выдержанных в H 2 O.

Для определения второго параметра к_хс образцы выдерживались в агрессивной среде (H 2 O) при температуре 20 ^оС. После каждого периодического извлечения композитов из среды измерялась масса, определялся предел прочности при сжатии и на растяжение при изгибе. График изменения прочности приведен на рис. 4. Аналитическое описание изменений прочности цементных композитов во времени под действием агрессивной среды можно производить с применением закона взаимодействия веществ (Гульдберга – Вааге):

ч9 = кс ^ с ^ с ^ , (5) где ^ - скорость взаимодействия; с 1 , с₂, с₃ - концентрация веществ; h,m,o - порядок реакции, к - константа.

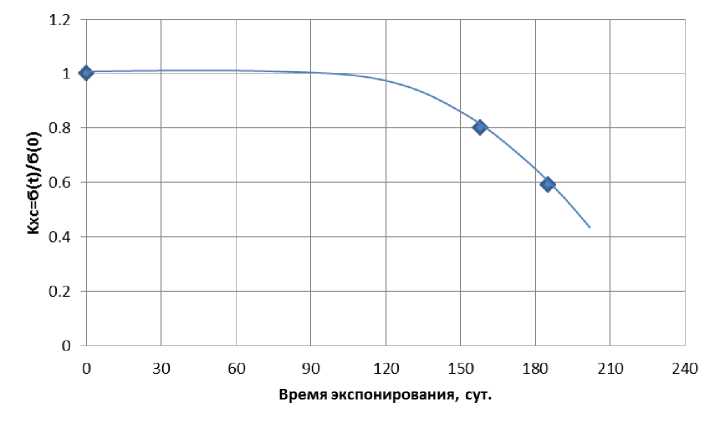
Рис. 4. Изменение прочности цементных образцов после экспонирования в воде.

Для обработки экспериментальных данных, представленных на рисунке 4, и определения параметра «k» произведем линеаризацию (рис. 5 – 7) рассматриваемой функции (5). Рассмотрим моно-, би- и тримолекулярные модели взаимодействия. В первом случае

\nKxcl = luC0-k1t,(6)

во втором –

1/KXC2 = 1/Co + k2t,(7)

в третьем –

1/Kx2c3 = 1/Co2 + 2k3t .(8)

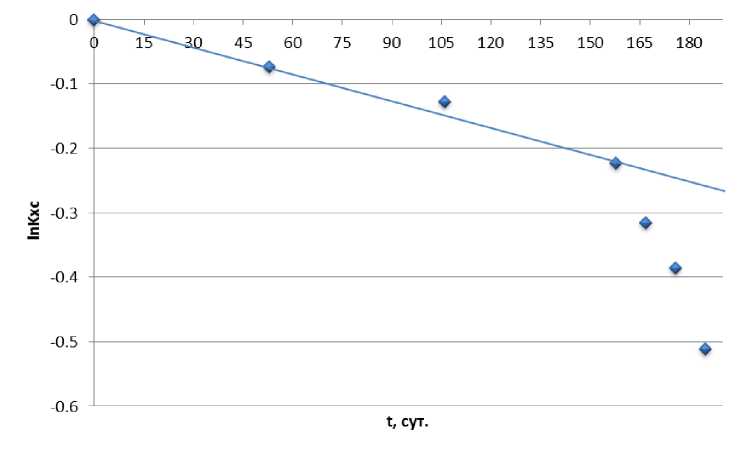
Рис. 5. Линеаризация мономолекулярной модели взаимодействия цементных образцов и воды.

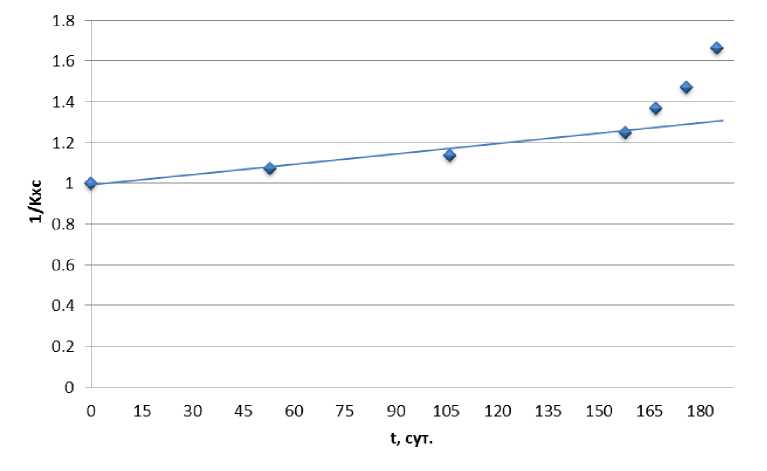
Рис. 6. Линеаризация бимолекулярной модели взаимодействия цементных образцов и воды.

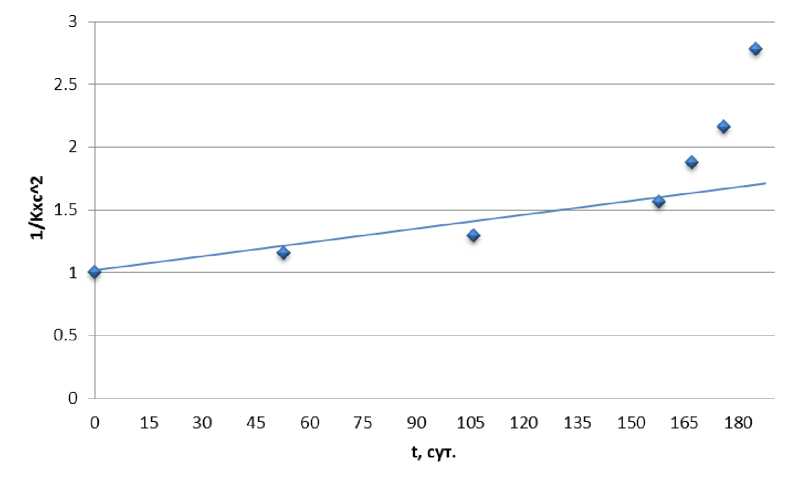
Рис. 7. Линеаризация тримолекулярной модели взаимодействия цементных образцов и воды.

Параметр «k» по уравнению (7) равен:

k2 = 0,002.                                     (9)

Результаты обработки экспериментальных данных с применением мономолекулярной модели показали, что она плохо описывает процесс деградации. В тоже время бимолекулярная модель более точно описывает результаты эксперимента.

Рассмотрено влияние воды на работу железобетонных конструкций.

Для оценки ресурса железобетонной плиты в качестве модели деградации, на основе которой будет производиться расчет, выбираем модель диффузионного типа (рис. 1) и соответствующую функцию деградации [9]:

D= — ^v o

±  М^-^*/*^ = 1_ £110-^)

1-O,5( o              1-0,5^₀

Данные для расчета: h = 7см, h o = 5,5см, класс бетона плиты B15, R_b = 8,5 МПа, R_bt =

0,75 МПа. Арматура рабочая - обыкновенная проволока периодического профиля Вр500 диаметром 4 мм в сварной рулонной сетке: Rs = 415 МПа.

R = 4 см, кхс = 0,002, м = 0,002 , t0,5 = 191.

Коэффициент диффузии равен:

D = 0,2 • — = 0,2 • — = 1,68 • 10-6 .

t o,s             191

Глубинный показатель определяем по формуле:

a = k(^)VDf = 0,1 • 71,68 -10-6-t ;

класса

^ 11 =

а _ 0,тУ1,б8Л0 ~ ⁶т

h o

0,055

= 1,8271,68 • 10-6 • t ;

^0= Mr; = 0,002-4^ = 0,0976 ;

D =^w = 1

^М (0)

-

^ 11 (1 К хс ) _ i

^1-0,5^ o

-

1,8271,68-10 -⁶ -t(1-0,002)

1-0,5-0,0976

.

По полученным значениям уравнения (15) строим график деградационной функции (рис. 8).

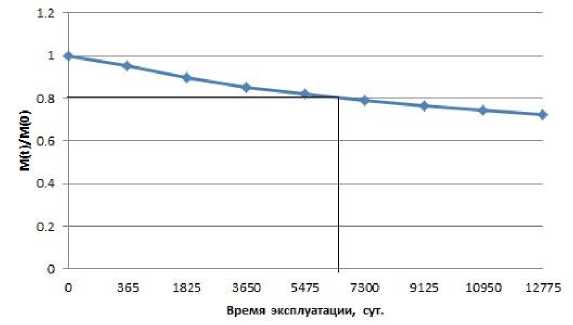
Рис. 8. Определение остаточного ресурса монолитной железобетонной плиты перекрытия методом деградационных функций.

По результатам проведенных исследований выявлено, что после примерно через 19 лет эксплуатации несущая способность плиты уменьшится на 20% и потребуется восстановление (ремонт) для дальнейшей нормальной эксплуатации данной конструкции. Поэтому для повышения ресурса данной конструкции необходимо обосновать выбор класса бетона и арматуры с учетом воздействия агрессивных сред.