Прогнозирование упругих характеристик армированного волокном пластика при изгибе: многомасштабное конечно-элементное моделирование и эксперимент

Объем применения полимерных композиционных материалов в строительстве, благодаря их уникальным свойствам [1–4], имеет большой потенциал роста.

Композит может быть сформирован из большого количества компонентов. В качестве матрицы могут применяться широко распространенные органические эпоксидные, фенольные, полиэфирные смолы и их комбинации, а также, например, неорганические или гибридные связующие [2,5–7]. В матрицу могут добавляться модифицирующие инертные и активные добавки, например, это могут быть минеральные порошки, углеродные нанотрубки, мелкодисперсные отходы или побочные продукты каких-либо производств и т. д. [8–12]. В качестве армирования могут использоваться нити или ткани на основе стеклянных, углеродных, базальтовых или органических волокон. Композиты могут быть также армированы дисперсными относительно короткими волокнами в том числе биологического происхождения [13–16]. Если мы имеем композит, в который входит более двух компонентов, определенным образом взаимодействующих между собой и посредством этого взаимодействия определяющих некоторые из его функциональных характеристик, то такой материал можно отнести к гибридным [5,17–19].

В отличие от традиционных строительных материалов, нормативные характеристики которых давно изучены и доступны проектировщикам, для большинства композитов (если не считать самый известный композит – железобетон) полная строительная база нормативных характеристик отсутствует и вряд ли скоро появится из-за большого многообразия компонентов для таких материалов. При этом в условиях повышающихся требований к ресурсосбережению необходимо максимально использовать любое имеющееся в наличии доступное по цене сырье, чтобы на выходе получить функциональную и экономически эффективную конструкцию из композитного материала.

Таким образом, задача прогнозирования эксплуатационных характеристик композитных материалов для применения их в области строительства является актуальной. При этом следует сосредоточиться не только на создании нормативной базы данных свойств, строго определенных по составу и структуре композитных материалов (которая пусть и в ограниченном виде также является необходимой), но и на получении методик для прогнозирования и быстрой идентификации механических характеристик композитов для строительства. Поскольку в других областях промышленности, таких как авиа- и машиностроение применение композитов более распространено, чем в строительстве, целесообразным представляется адаптация существующих методик, возможно с введением некоторых допущений и упрощений с обеспечением приемлемой для строительных конструкций точности (требования к которой высоки, но не настолько как в авиа- и машиностроении).

Моделирование композитов можно рассматривать на разных масштабах, при этом необходимо найти уровень детализации, обеспечивающий с приемлемой для строительных конструкций точностью и надежностью прогнозирование их поведения при эксплуатационных воздействиях. В настоящее время активно развивается подход разномасштабного конечноэлементного моделирования с применением конечноэлементной гомогенизации [20–22], позволяющий достаточно точно прогнозировать механические характеристики композитов с учетом их наиболее значимых структурных особенностей. Развиваются также аналитические структурные модели прогнозирования свойств композитов, например описанные в [23–27].

Достаточно широко распространены и имеют перспективу расширения области применения в строительстве крупногабаритные оболочечные конструкции из композитов [1,3,4,28–35]. Они применяются в сооружениях газоотводящих трактов, трубопроводах различного назначения, резервуарах и т. п. В таких конструкциях для несущих стеклопластиковых слоев наиболее важными являются изгибные механические характеристики (прочность и жесткость). Технологические режимы и допуски к изготовлению стеклопластиковых оболочек для строительных сооружений являются более «мягкими», по сравнению, например, с авиационными конструкциями, что обусловлено экономическими причинами [1]. Поэтому необходимо иметь методику прогнозирования механических свойств стеклопластиков, формирующих такие оболочки, с учетом их фактических структурных особенностей, определяемых технологией изготовления конкретного производителя и применяемыми материалами.

Настоящая работа посвящена изучению и верификации методики прогнозирования модуля упругости при изгибе стеклопластиков на основе стеклоткани и термореактивного полимерного связующего при помощи разномасштабного численного моделирования методом конечноэлементной гомогенизации с последующим переходом к структурно-феноменологической модели слоистого композита. В рамках апробирования методики необходимо было выполнить экспериментальную проверку результатов численного моделирования. После сопоставления результатов численного моделирования и эксперимента были выполнены численные исследования влияния параметров слоистой структуры стеклопластиковых образцов на их изгибную жесткость и оценка возможности введения некоторых упрощений при моделировании.

• 2    Materials and Methods

  2.1    Материалы

В работе рассмотрен стеклопластик, выполненный на основе стеклоткани ЭЗ-200 и эпоксидного связующего горячего отверждения.

Эпоксидное связующее (ЭС) для стеклопластика изготавливалось на основе эпоксидной смолы KER 828 (Южная Корея), являющейся аналогом российской смолы ЭД-20, в качестве отвердителя применялся изометилтетрагидрофталевый ангидрид (ИЗОМТГФА), в качестве ускорителя отверждения применялся 2,4,6-трис - (диметиламинометил) - фенол, выпускаемый под торговой маркой Алкофен. Соотношение по массе компонентов ЭС следующее: KER 828–54.5 %, ИЗОМТГФА – 42.5 %, Алкофен – 3 %.

Стеклоткань ЭЗ-200 выпускается согласно ГОСТ 19907–83 [36] и имеет следующие характеристики:

• -    толщина 0,190 +0.01 / -0.02 мм;

• -    поверхностная плотность 200 +16 / -10 г / м²;

• -    количество нитей на 1 см ткани по основе 10 +/- 1;

• -    количество нитей на 1 см ткани по утку 9 +/- 1;

• -    переплетение – полотняное;

• -    замасливатель – парафиновая эмульсия.

  

  Рис. 1 - Структура стеклоткани ЭЗ-200 Fig. 1 - Glass cloth EZ-200

  
  
2.2    Методика экспериментально-теоретических исследований деформационных характеристик и структуры материалов

Образцы стеклопластика изготавливались в виде пластин размерами 15 х 15 см. Вырезанные листы стеклоткани для удаления парафинового замасливателя непосредственно перед пропиткой связующим прокаливались при температуре 300оС. Всего в образцах было по 10 слоев стеклоткани, уложенных по схеме 0/90 (основа/уток). Образцы стеклопластика отверждались при температуре 120оС в течение 20 минут в силиконовых формах с пригрузкой через металлические пластины с тефлоновым покрытием под давлением около 0,22 кПа, затем отвержденные образцы выдерживались при температуре 150оС в течение 12 часов. После этого из пластин в направлении главных осей ортотропии вырезались балочные образцы, рассмотренные в настоящей работе. Балочные образцы эпоксидного связующего отверждались в силиконовых формах при том же режиме, что и образцы стеклопластика.

Испытания образцов стеклопластика и отвержденного эпоксидного связующего на трехточечный изгиб проводились согласно ГОСТ Р 56810–2015 [37] на машине Tinius Olsen h100ku. По паспортным данным точность измерения нагрузки машины Tinius Olsen h100ku составляет ± 0,5% в диапазоне от 0,2 до 100% от допустимой нагрузки установленного датчика силы (100 кН). Разрешающая способность измерения перемещения траверсы - 0,001 мм с Mishnev, M.V., Zadorin A. A., Khoroshilov N. A.

Prediction of elastic characteristics of fiberglass in bending: multi-scale finite element modeling and experiment;

погрешностью до 0,01 мм. Чтобы исключить влияние податливости машины, смещение центральной точки образца под нагрузкой также контролировались с помощью механического индикатора часового типа, установленного под образцом. Разница показаний перемещений по траверсе и индикатору часового типа не превышала 2%. Образцы испытывались на пролете 70 мм.

Рис. 2 - Внешний вид образцов

Fig. 2 - Sample appearance

Вычисление деформационных характеристик стеклопластика на эпоксидном связующем было выполнено в академической версии конечно-элементного пакета ANSYS с использованием встроенного модуля Material Designer. Вычисление упругих характеристик тканого композита производилось на основе метода конечно-элементной (КЭ) гомогенизации [20,21]. В рамках данного метода выделяется малый представительный объем материала (Representative Volume Element (RVE)), при этом имеющий достаточные размеры для обладания макроскопическими характеристиками упругих свойств. Прогнозированию механических характеристик полимерных композитов с использованием разномасштабного моделирования и конечноэлементной гомогенизации посвящены работы [20–22,38–40].

В модуле Material Designer пакета Ansys Workbench на основе заданных характеристик материала матрицы и наполнителя в виде ткани автоматически строится объемная КЭ модель элементарной ячейки и рассчитываются ортотропные или полностью анизотропные упругие характеристики гомогенизированного материала. При таком способе моделирования учитывается изогнутость нити в структуре ткани, а также влияние поперечных нитей на модуль упругости в продольном направлении.

В качестве исходных данных для создания модели в модуле Material Designer задавались вышеприведенные упругие характеристики стекловолокна, упругие характеристики отвержденной эпоксидной матрицы из той же партии, на которой изготавливался стеклопластик, были определены методом трехточечного изгиба. При комнатной температуре модуль упругости составил 3000 МПа, коэффициент Пуассона был принят равным 0,35, плотность, определенная гидростатическим взвешиванием, составила 1200 кг/м3.

Вычисление характеристик происходит с учетом следующих допущений:

• -    моделируемый волокнистый композит состоит из изотропного линейно-упругого материала матрицы и изотропного или трансверсально-изотропного линейно-упругого материала нитей;

• -    объемная доля волокон в нитях постоянна;

• -    представительный объем материала является строго периодическим.

В качестве исходных данных для модели типа woven composite задаются следующие параметры:

• -    Weaving type – тип плетения ткани (полотняный или саржевый);

• -    Fiber volume fraction – доля объема волокна от объема всего RVE;

• -    Yarn fiber volume fraction – доля объема внутри отдельной нити, которую занимает материал волокон (стекло в нашем случае), объем нити «нетто»;

• -    Shear angle – угол в градусах перекоса волокон из-за драпировочных свойств ткани;

• -    Yarn spacing – расстояние между центрами поперечных сечений соседних нитей;

• -    Fabric thickness – толщина моделируемого RVE;

• -    Repeat count – количество элементарных ячеек, учитываемых в модели в направлении каждой координаты;

• -    Align with x direction – волокна ориентируются вдоль оси X (если нет, то ориентируются

  

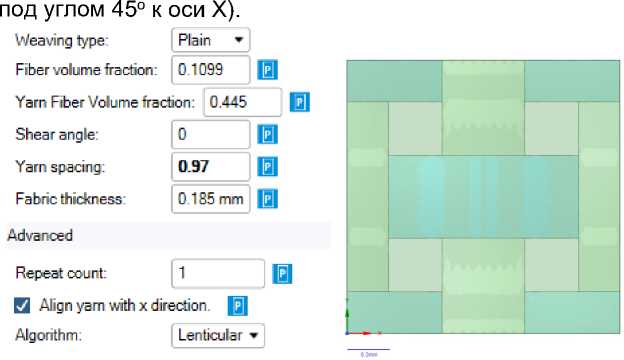
  Рис. 3 - Исходные данные для построения геометрии, геометрическая и конечноэлементная модели RVE

  Fig. 3 - Initial data for constructing geometry, geometric and finite element RVE models

  
  
  
  
  

Как следует из справочной системы параметр Fiber volume fraction определяется как произведение параметра Yarn volume fraction на параметр Yarn fiber volume fraction (см. расшифровку выше). Параметр Yarn volume fraction не задается напрямую, он соответствует доле объема «брутто» всех нитей (без учета пространства между отдельными волокнами, составляющими нить) относительно объема RVE. Параметр Yarn volume fraction можно определить как отношение площади «брутто» поперечных сечений нитей, ориентированных вдоль образца, к площади поперечного сечения образца.

Моделирование трёхточечного изгиба стеклопластиковых образцов, результаты которого сопоставлялись с экспериментом, выполнялось в академической версии пакета Ansys APDL. Образцы моделировались оболочечными элементами Shell181 [41], поддерживающими многослойные сечения.

Исследование мезоструктурных особенностей рассмотренных образцов стеклопластиков выполнялось при помощи снабженных цифровыми камерами оптических микроскопов Levenhuk DTX 90 и Levenhuk 320 BASE. Микроскоп Levenhuk DTX 90 использовался для уточнения фактических толщин слоев в структуре стеклопластика и для определения величины параметра Yarn volume fraction (доля площадей «брутто» сечений нитей от площади сечения элемента). Микроскоп Levenhuk 320 BASE с увеличением 40:1 в проходящем светеиспользовался для определения параметра Yarn fiber volume fraction (доля стекловолокон в объеме нити) на полоске стеклопластика толщиной 1,5 мм вырезанной параллельно поперечному сечению образца.

Полученные цифровые фотографии структуры образцов стеклопластика импортировались в пакет NanoCAD СПДС (версия для образовательных учреждений) и приводились к одному масштабу. За базовый размер принималась толщина образца в отмеченной точке, которая измерялась штангенциркулем с точностью до 0,05 мм. После приведения к одному масштабу проводилась оценка толщин слоев, формы и размеров нитей, долей занимаемого нитями пространства внутри образцов ( Yarn volume fraction) , долей занимаемого волокнами пространства внутри нитей ( Yarn fiber volume fraction ). Также для сопоставления с реальной структурой образцов импортировалось и масштабировалось изображение геометрической модели RVE из модуля Design Modeler.

В данной работе ставилась задача прогнозирования при помощи численного моделирования характеристик конкретного образца с учетом его индивидуальных структурных особенностей, поэтому статистическая обработка не требовалась и были рассмотрены всего два образца с отличиями в толщинах слоёв, их структура показана на фото (Рис. 4 ,Fig. 4) .

Методом гидростатического взвешивания была определена плотность отвержденного связующего, составившая в среднем 1200 кг/м3, а также плотность стеклопластика, составившая в среднем по двум образцам 1604 кг/м3.

• 3    Results and Discussion

  3.1    Оценка структурных параметров стеклопластиков и определение исходных данных для моделирования

Структура образцов на мезоуровне была исследована для определения значений параметров, необходимых для построения конечноэлементной модели RVE в модуле Design Modeler пакета Ansys.

На рисунке (Рис. 4, Fig. 4) показаны фрагменты продольных сечений рассмотренных образцов №1 и 2. Микрофотографии сделаны в точках, где было произведено измерение толщин, по значениям которых производилось приведение к единому масштабу. На данных фото выделены сечения продольных армирующих нитей и прослоек смолы между ними. Контуры нитей имеют различную толщину т. к. в сечение попали их разные по толщине участки.

Хотя образцы вырезались из одной пластины их средние толщины различаются примерно на 12%, при этом образец №1 имеет нижний утолщенный по сравнению с остальными слой смолы со средней толщиной около 0,26 мм, что вероятно связано с местными неровностями подложки из пропитанной тефлоном стеклоткани, на которую выкладывался образец. Если не принимать этот слой в расчет, то разница по толщине составит около 2%.

На рисунке (Рис. 5, Fig. 5) показано поперечное сечение образца №1, на нем выделены внешние контуры попавших в сечение продольных нитей и приведены некоторые основные размеры.

Чтобы оценить среднюю площадь «брутто» нити в поперечном сечении был выделен прямоугольный участок размерами 2,6 х 5,2 мм, и средняя площадь «брутто» нити определялась как среднее арифметическое суммарной площади всех нитей, которые целиком оказались внутри этого участка. Определенная таким образом, осредненная площадь «брутто» одной нити составила 0,0636 мм2.

Значение параметра Yarn volume fraction определенное как отношение суммарной площади «брутто» всех нитей к площади выделенного прямоугольного участка размерами 2,6 х 5,2 мм составило 0,247.

На рисунке (Рис. 6, Fig. 6) показаны фактические расстояния между центрами продольных нитей, осредненное значение этих расстояний составило 0,97 мм и было принято в качестве значения параметра Yarn spacing .

На рисунке (Рис. 7, Fig. 7) показана микрофотография в проходящем свете фрагмента поперечного сечения, на котором отображаются продольные и поперечные нити, в сечении продольных нитей можно выделить отдельные стеклянные волокна. Измеренный по масштабированной микрофотографии диаметр отдельных стеклянных волокон составил около 0,008 мм. Для определения доли площади волокон внутри площади «брутто» нити на каждое волокно наносился заштрихованный круг диаметром 0,008 мм, после чего значение параметра Yarn fiber volume fraction определялось как отношение суммарной площади заштрихованных кругов к площади «брутто» нити. Среднее значение) параметра Yarn fiber volume fraction, определенное по двум нитям, показанным на рисунке (Рис. 7, Fig. 7) , составило (0,474 + 0,422)/2=0,445.

В итоге было определено значение параметра Fiber volume fraction как произведение Yarn fiber volume fraction на Yarn volume fraction, оно составило 0,1099.

(a)

(b)

Рис. 4 - Фотографии мезоструктуры продольных сечений исследуемых образцов стеклопластика: a) образец №1; b) образец №2

Fig. 4 - Photos of the mesostructure of longitudinal sections investigated samples of fiberglass: a) sample no. 1; b) sample no. 2

Рис. 5 - Микрофотография поперечного сечения стеклопластикового образца №1 с выделением сечений «брутто» продольных нитей

Fig. 5 - Micrograph of the cross-section of the fiberglass sample No. 1 with the highlighting of the "gross" sections of the longitudinal threads

Рис. 6 - Микрофотография поперечного сечения стеклопластикового образца №1 с фактическими расстояниями между центрами продольных нитей

Fig. 6 - Micrograph of the cross-section of fiberglass sample No. 1 with the actual distances between the centers of the longitudinal threads

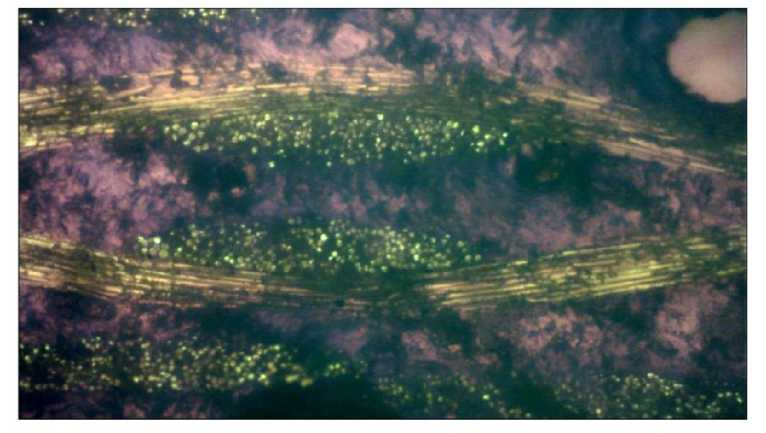
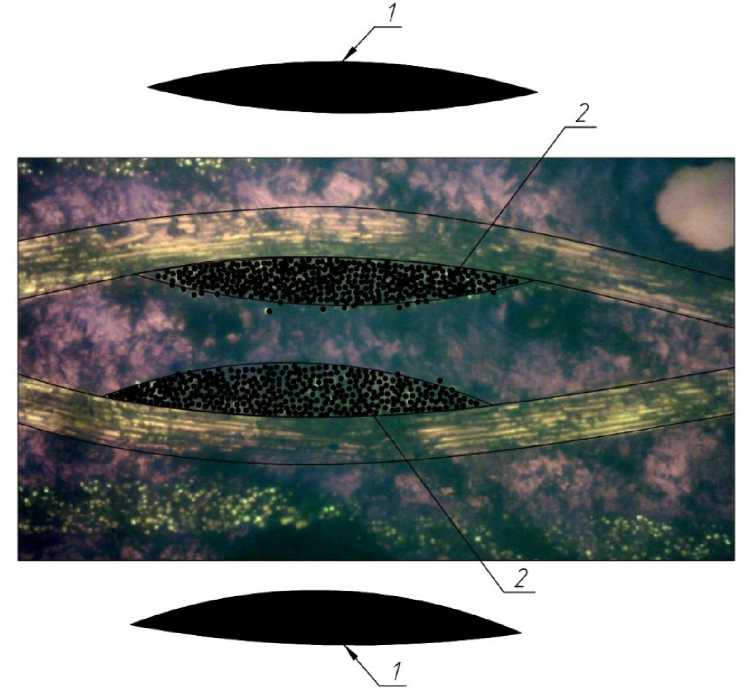
Рис. 7 - Микрофотография фрагмента поперечного сечения образца (продольные и поперечные нити): 1) выделенная площадь «брутто» продольной нити; 2) примерное распределение волокон внутри нити

Fig. 7 - Micrograph of a fragment of the cross-section of the sample (longitudinal and transverse threads): 1) the allocated area "gross" of the longitudinal thread; 2) the approximate distribution of fibers within the thread

3.2    Вычисление упругих констант стеклопластика

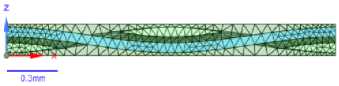
На основании значений параметров, полученных из анализа микрофотографий структуры образцов, модулем Material Designer пакета Ansys Workbench были сформированы геометрические и конечноэлементные модели элементарных ячеек стеклопластика. Всего было сформировано и рассчитано три модели, показанных на рисунке (Рис. 8, Fig. 8) , отличающихся количеством элементарных ячеек вдоль каждой координаты. На рисунке (Рис. 9, Fig. 9) показано сечение геометрической модели, включающей две элементарных ячейки вдоль каждой координаты. Приведенная площадь сечения одной нити в модели составила 0,0224 мм², что достаточно близко к значению 0,445 * 0,0636 мм² = 0,0283 мм² (среднее значение площади стекловолокон внутри площади «брутто» нити), определенному по микрофотографиям.

(a)

(b)

(c)

Рис. 8 - Объемные конечноэлементные модели RVE с разным количеством учитываемых ячеек вдоль координатных осей: a) одна ячейка b) две ячейки c) три ячейки

Fig. 8 - Solid finite element RVE models with a different number of cells taken into account along the coordinate axes: a) one cell b) two cells c) three cells

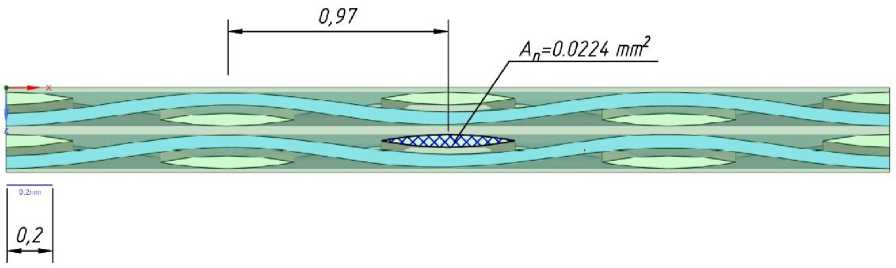
Рис. 9 - Геометрическая модель RVE на примере построения 2-х ячеек Fig. 9 - Geometric model of RVE on the example of constructing 2 cells

Результаты расчета ортотропных характеристик стеклопластика для различного количества учитываемых элементарных ячеек ((a) – 1 ячейка, (b) – 2 ячейки, (c) – 3 ячейки) в модуле Design Modeler представлены на рисунке (Рис. 10, Fig. 10) .

Значения механических характеристик практически не отличаются во всех трех случаях, поэтому для условий подобных рассмотренным в настоящей работе не имеет смысла выполнять расчет более, чем одной ячейки, поскольку размер конечноэлементной модели при увеличении количества учитываемых ячеек возрастает в геометрической прогрессии.

Mishnev, M.V., Zadorin A. A., Khoroshilov N. A.

Prediction of elastic characteristics of fiberglass in bending: multi-scale finite element modeling and experiment;

			Engineering Constants
Weaving type:	Plain v		El	14394E+10	Pa
Fiber volume fraction:	0.1099	0	E2	14395E+10	Pa
Yarn Fiber Volume fraction 0.445		[Ц	E3	5.6226ЕЯИ	Pa
			G12	3.9559E*09
Shear angle:	0	0
			G23	1.5701E#09	Pa
Yam spacing:	0.97 mm	0	G31	1 5701E4J9	Pa
Fabric thickness	0.185 mm	El	nu12	0.19052
Advanced	—		nu13	0.38694
			nu23	0.38694
Repeat count:	1	10	Density
Q Align yam with x direction. И			*ю	1545.5	kg m*-3
			Fabric Fiber Angle
Algorithm:	Lenticular
		5	phi		degree

(a)

Weaving type:	Plain ’		Engineering Constants
Fiber volume fraction:	0.1099	0	E1	1.4403E+10	Pa
		0	E2	1.4403E+10	Pa
			E3	5.6234E*09	Pa
Shear angle:		0
	0		G12	3.9585E*09	Pa
Yarn spacing:	0.97 mm	0	G23	1.5703E*09	Pa
Fabric thickness:	0.185 mm	0	G31	1.5703E*09	Pa
			nu12	0.19057
Advanced			nu13	0 38686
Repeat count:	I2	]0	nu23	0 38686

Q Align yam with x direction И           rho                  1545Б               kgm"-3

Algorithm:	Lenticular »	Fabric Fiber Angle
		phi	1	degree

(b)

Weaving type:	Plain •
Fiber volume fraction:	0.1099	0
Yam Fiber Volume fraction: 0.445		0
Shear angle:	0	0
Yam spacing:	0.97 mm	0
Fabric thickness:	0.185 mm	0
Advanced
Repeat count:	3	10
Q Align yam with x direction. 0
Algorithm:	Lenticular

Engineering Constants

El	1.4407E+10	Pa
E2	1.4407E+10	Pa
E3	5.6239E+09	Pa
G12	3.9618E+09	Pa
G23	1.5705E+09	Pa
G31	1.5705E+09	Pa
nu12	0.1906
nu13	0.38682
nu23	0.38682

Density

rho	1545.5	| kg пГ-3
Fabric Fiber Angle
[phi		degree

(c)

Рис. 10 - Результаты расчета упругих констант для RVE:

• (a) одна элементарная ячейка; (b) две элементарных ячейки; (c) три элементарных ячейки Fig. 10 - Results of calculation of elastic constants for RVE:

• (a) single unit cell; (b) double unit cells; (c) three unit cells

  Также в модуле Material Designer рассчитана средняя плотность элементарных ячеек (RVE), которая составила 1545,5 кг/м³, что достаточно близко к значению плотности рассматриваемых стеклопластиковых образцов – 1604 кг/м³, определенному гидростатическим взвешиванием.

3.3    Результаты экспериментального определения модуля упругости при изгибе 3.4    Результаты конечноэлементного моделирования изгиба стеклопластиковых образцов

Разница расчетным и фактическим значением плотности составила около 4%, что косвенно подтверждает, хорошую точность определения по микрофотографиям объемных долей материала матрицы и армирующего наполнителя и адекватность построения конечноэлементной модели для RVE.

По методике [37], описанной в разделе 2, были определены приведенные модули упругости образцов стеклопластика при изгибе, для образца №1.1 он составил 10110 МПа, для образца №1.2 – 12700 МПа. Образец №1.1 имел размеры поперечного сечения в средней части 2,6 х 18,95 мм, образец № 1.2 – 2,15 х 17,85 мм.

Полученные значения приведенных модулей упругости будем использовать для оценки результатов конечноэлементного моделирования изгиба стеклопластиковых образцов.

Конечноэлементное моделирование изгиба стеклопластиковых образцов проводилось в модуле Ansys APDL, образцы моделировались оболочечным элементом Shell181 с поддержкой многослойных сечений. Длина модели изгибаемого образца между закреплениями принята 70 мм. Образец шарнирно закреплен от по трем поступательным перемещениям на одной из опор и по вертикальному поступательному перемещению на второй опоре. Нагрузка на образец задана в виде сосредоточенной силы 100 кН (10 кгс), приложенной в середине пролета.

В таблице (Таблица 1, Table 1) показаны варианты рассмотренных конечноэлементных моделей стеклопластика.

Модели 1.1, 2.1 – однослойные, толщиной соответствующей толщине испытанных стеклопластиковых образцов, изотропные с модулем упругости соответствующим значению, полученному при эксперименте для каждого из образцов.

Модели 1.2, 2.2 – однослойные, толщиной соответствующей толщине испытанных стеклопластиковых образцов, изотропные с модулем упругости соответствующим значению, полученному из результатов расчета в модуле Material Designer.

Модели 1.3, 2.3 – многослойные, суммарная толщина слоев соответствует толщине испытанных стеклопластиковых образцов. Модель состоит из чередующихся изотропных монослоёв – армированных (условно) и неармированных. Модуль упругости армированных слоев принят согласно результатам расчета в модуле Material Designer, модуль упругости промежуточных неармированных слоев принят равным модулю упругости эпоксидной смолы. Толщина армированных слоёв принята с учетом результатов микроскопических исследований 0,185 мм, толщина неармированных слоев принята одинаковой из расчета по формуле 1:

t m = ( T - t a • П )/( П + 1)                                                     (1)

Где T – общая толщина образца, t a – толщина одного армированного слоя, n – количество армированных слоев.

Модель 1.4 отличается от модели 1.3 толщиной нижнего неармированного слоя, толщина которого принята равной 0,26 мм согласно микроскопическим исследованиям структуры данного конкретного образца. Толщина остальных неармированных слоев принята одинаковой из расчета по формуле 2:

= ( T-t ■ n)/n                                               (2)

ma

Где T – общая толщина образца, t a – толщина одного армированного слоя, n – количество армированных слоев.

Модели 1.5, 2.4 – однослойные, толщиной соответствующей толщине испытанных стеклопластиковых образцов, ортотропные с упругими константами соответствующим значениям, полученным из результатов расчета в модуле Material Designer.

Модели типа 1.1, 1.2, 1.5, 2.1, 2.2, 2.4 – можно отнести к феноменологическим, а модели 1.3, 1.4, 2.3 – к структурно-феноменологическим [42–44].

Таблица 1 Варианты рассмотренных конечноэлементных моделей стеклопластика

Table 1 Variants of the considered finite element models of fiberglass

№ модели	Сечение	Тип анизотропии	Толщина слоев	Упругие характеристики
1.1	Однослойное	Изотропный	2,6 мм	E=10100 МПа, nu = 0,35
1.2	Однослойное	Изотропный	2,6 мм	E=14390 МПа, nu = 0,35
1.3	Многослойное	Изотропный	Армированные слои: 0,185*10=1,85 мм	E a =14390 МПа, nu a = 0,35
			Неармированные слои: 0,06818*11=0,75 мм	E m =3000 МПа, nu m = 0,35
1.4	Многослойное	Изотропный	Армированные слои: 0,185*10 = 1,85 мм	E a =14390 МПа, nu a = 0,35
			Неармированные промежуточные слои: 0,049*10=0,49 мм	E m =3000 МПа, nu m = 0,35
			Неармированный нижний слой: 0,26*1=0,26 мм	E m =3000 МПа, nu m = 0,35
1.5	Однослойное	Ортотропный	2,6 мм	E 1 =14390 МПа E 2 =14390 МПа E 3 =5622 МПа G 12 =3955 МПа, nu 12 = 0,1905 G 23 =1570 МПа, nu 13 = 0,3869 G 31 =1570 МПа, nu 23 = 0,3869
2.1	Однослойное	Изотропный	2,15 мм	E=12700 МПа, nu = 0,35
2.2	Однослойное	Изотропный	2,15 мм	E=14390 МПа, nu = 0,35
2.3	Многослойное	Изотропный	Армированные слои: 0,185*10 = 1,85 мм	E a =14390 МПа, nu a = 0,35
			Неармированные слои: 0,02727*11=0,3 мм	E m =3000 МПа, nu m = 0,35
2.4	Однослойное	Ортотропный	2,15 мм	E 1 =14390 МПа E 2 =14390 МПа E 3 =5622 МПа G 12 =3955 МПа, nu 12 = 0,1905 G 23 =1570 МПа, nu 13 = 0,3869 G 31 =1570 МПа, nu 23 = 0,3869

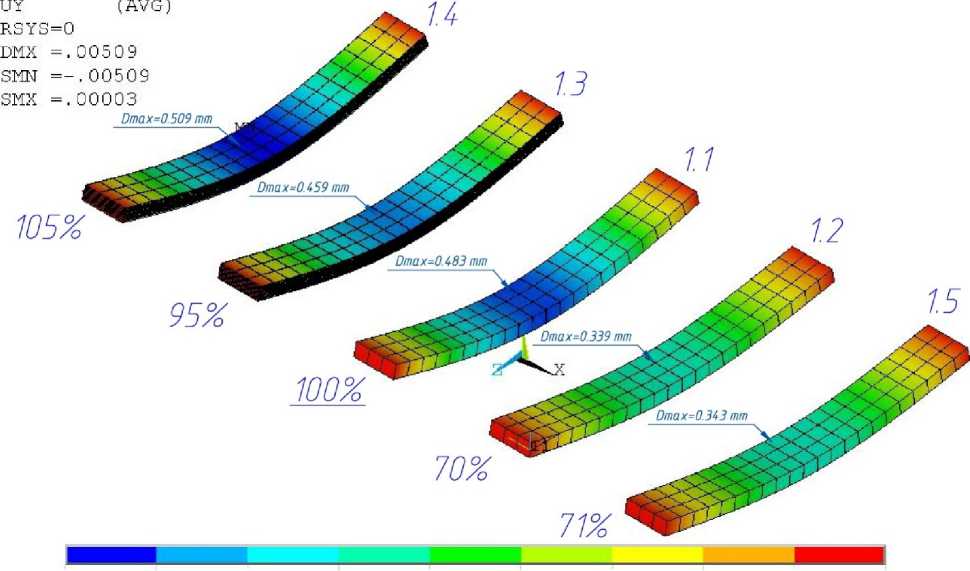
-.00509        -.00395        -.00281        -.00168        -.00054

-.00452        -.00338        -.00225        -.00111        .00003

Рис. 11 - Результаты расчета деформаций образца №1 с использованием различных моделей

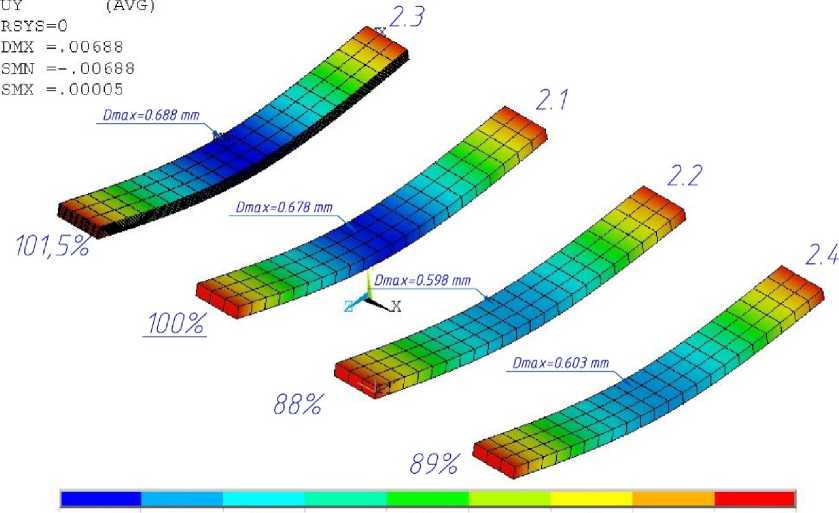
-.00688        -.00534        -.0038         -.00226        -.00072

- ПОК11        -00457       -№ОЯОЧ       -.00149        .ППППС

Рис. 12 - Результаты расчета деформаций образца №2 с использованием различных моделей Fig. 12 - Results of calculating deformations of sample No. 2 using different models

Экспериментальным результатам испытаний на трехточечный изгиб соответствуют результаты расчета моделей образцов №1.1 и 2.1 поэтому они приняты за базовые.

Модели под №1.2 и 2.2 являются изотропными и однослойными (квазиоднородными), модуль упругости принят по результатам конечноэлементного моделирования и расчета упругих констант одной ячейки (или армированного монослоя) в модуле Material Designer.

Модели под №1.5 и 2.4 являются ортотропными и однослойными (квазиоднородными), упругие константы приняты по результатам конечноэлементного моделирования и расчета одной ячейки (или, что то же самое одного армированного монослоя с периодическим и регулярным расположением ячеек) в модуле Material Designer.

Толщины сечений в однослойных моделях соответствовали толщинам экспериментально испытанных образцов (2,6 мм для образца №1, 2,15 мм для образца №2).

Результаты расчетов показывают, что для более толстого образца №1 отклонение от результатов эксперимента при расчете по модели 1.2 составило около 30%, учет ортотропии при расчете по модели 1.5 также дал существенное отклонение от эксперимента в 29%. Для образца №2 с более тонкими прослойками смолы между армированными слоями отклонение результатов от эксперимента при расчетах по моделям №2.2 и 2.4 составило 11 и 12%, что существенно ниже, чем для первого образца, но все равно достаточно много.

Модели под №1.3, 1.4 и 2.3 являются многослойными с изотропными материалами слоев. В моделях чередуются армированные слои со слоями неармированной смолы (матрицы). Упругие характеристики неармированных слоев соответствуют изотропным упругим характеристикам эпоксидной смолы горячего отверждения, упругие характеристики армированных слоев заданы по результатам моделирования монослоя в модуле Design Modeler.

Толщина армированных слоев принята равной для всех моделей 0,185 мм, как и в модуле Material Designer. Толщина неармированных слоев для моделей 1.3 и 2.3 принималась одинаковой и рассчитывалась исходя из фактической толщины образцов (см. выше). Для модели нижний неармированный слой был принят равным осредненной величине 0,26 мм (исходя из анализа микрофотографий), для остальных неармированных слоев также принята одинаковая толщина.

Результаты расчетов показывают, что отклонение от эксперимента при расчетах по моделям 1.3 и 1.4 не превышает 5% (образец №1), а по модели 2.4 – не превышает 1,5% (образец №2).

• 4    Conclusions

Исходя из вышеприведенных результатов можно сделать следующие выводы и рекомендации:

• 1.    В модуле Material Designer пакета Ansys Workbench на основе упругих характеристик материалов исходных компонентов (матрицы и волокна), а также объемной доли волокна и геометрических параметров армирующего тканого наполнителя, достаточно точно можно определить упругие характеристики элементарной ячейки (монослоя) композита на основе полимерной матрицы (например, эпоксидной) и тканого армирующего наполнителя (например, из стеклоткани).

• 2.    Увеличение количества моделируемых элементарных ячеек в пределах RVE существенно не влияет на значения вычисляемых упругих характеристик (по крайней мере при исходных предпосылках, принятых в настоящей работе), но существенно увеличивает размерность модели и затраты вычислительных ресурсов. Поэтому наиболее рациональным будет использовать данную методику для определения характеристик монослоя, которые в дальнейшем будут использоваться в структурно-феноменологических моделях, учитывающих фактическую слоистую структуру композита, которая может отличаться в зависимости от применяемой технологии или режима изготовления.

• 3.    С учетом полученных результатов можно рекомендовать простую методику прогнозирования деформативности композитов на основе тканых армирующих наполнителей (с допущением о близких механических характеристиках всех армированных слоев по толщине), состоящую из следующих этапов:

• -    задание физико-механических характеристик свойств исходных компонентов (матрицы и волокна);

• -    задание в качестве исходных данных для формирования модели элементарной ячейки тканого композита осредненных параметров его структуры (объемной доли волокон, расстояния

между нитями), они могут быть получены по результатам микроскопических исследований, с использованием достаточно простых оптических микроскопов с увеличением до 40 крат;

• -    определение упругих констант армированного монослоя (с толщиной равной толщине применяемой стеклоткани) по методу конечноэлементной гомогенизации, например, с использованием модуля Material Designer пакета Ansys;

• -    создание простой конечноэлементной модели слоистого композита, включающей необходимое количество квазиоднородных армированных и неармированных слоев, при этом толщину неармированных слоев допускается принимать осредненной, определяемой по формуле 1;

• -    при наличии в структуре слоев, толщина которых существенно отличается от остальных их рекомендуется учитывать отдельно, при этом критерий «существенности» требует уточнения;

• -    уточнение жесткости проектируемого композита и определение (путем решения обратной задачи) его упругих констант при помощи моделирования какого-либо механического испытания, например, трехточечного изгиба.

• 4.    Результаты разномасштабного моделирования по вышеописанной методике показали хорошее совпадение с экспериментом, на примере стеклопластиковых образцов на основе стеклоткани ЭЗ-200 и эпоксидного связующего горячего отверждения. Разница между прогнозными и экспериментальными деформациями образцов составила от 1,5 до 5%.

• 5.    Применение подобной методики позволяет определять механические характеристики композитов с учетом их индивидуальных структурных особенностей, таких как, например, разная толщина прослоек смолы между армированными слоями. Тогда как, например, модуль Material Designer (в настоящее время) позволяет прогнозировать свойства композитов только со строго регулярной по толщине структурой.

• 6.    В дальнейшем перспективным представляется применение данной методики для прогнозирования характеристик гибридных композитов, например на основе наполненной матрицы и гибридного (комбинированного) армирования. В качестве гибридного армирования могут быть рассмотрены, например чередующиеся слои угле- и стеклоткани, либо стеклоткани и металлической сетки и т. п.

• 5    Acknowledgments

  Работа выполнена в рамках государственного задания FENU-2020–0019 Министерства науки и высшего образования Российской Федерации.

• 6    References

  • 1.    V.M. Astashkin, V.S. Zholudov. Chimneys and elements of gas-escape paths made of polymer composites. Gysev B.V. Chelyabinsk–Moscow–Safonovo, 2011.–155 p.

  • 2.    Fangueiro R. Fibrous and Composite Materials for Civil Engineering Applications / Fibrous and Composite Materials for Civil Engineering Applications. 2011.

  • 3.    Alperin V.I., Korolkov N. v. Konstrukcionnye stekloplastiki. Moscow: Chemistry, 1979. 1–360 p.

  • 4.    McKenna J.C. Big and tall composite structures / NACE - International Corrosion Conference Series. 2000.

  • 5.    Starovoytova I.A. et al. Hybrid organic-inorganic binders received by a sol-gel process and their practical application in composition materials / Izvestiya Kazanskogo gosudarstvennogo arhitekturno-stroitelnogo universiteta. 2010. No. 2 (14).

  • 6.    Abd El-baky M.A. Evaluation of mechanical properties of jute/glass/carbon fibers reinforced hybrid composites // Fibers and Polymers. 2017. Vol. 18, No. 12. P. 2417–2432.

  • 7.    Saba N., Jawaid M. Epoxy resin based hybrid polymer composites / Hybrid Polymer Composite Materials: Properties and Characterisation. 2017.

  • 8.    Zhang Y., Rhee K.Y., Park S.J. Nanodiamond nanocluster-decorated graphene oxide/epoxy nanocomposites with enhanced mechanical behavior and thermal stability / Composites Part B: Engineering. 2017.

  • 9.    Kim S.K. et al. Thermal and mechanical properties of epoxy/carbon fiber composites reinforced with multi-walled carbon nanotubes / Journal of Macromolecular Science, Part B: Physics. 2012.

  • 10.    Yang P. et al. Preparation and thermo-mechanical properties of heat-resistant epoxy/silica hybrid materials / Polymer Engineering and Science. 2008.

  • 11.    Sui G. et al. Enhancing mechanical properties of an epoxy resin using “liquid nano-reinforcements” / Materials Science and Engineering A. 2009.

  • 12.    Domun N. et al. Improving the fracture toughness and the strength of epoxy using nanomaterials-a review of the current status / Nanoscale. 2015. Vol. 7, No. 23.

  • 13.    de Azevedo A.R.G. et al. Natural fibers as an alternative to synthetic fibers in reinforcement of geopolymer matrices: A comparative review / Polymers. 2021. Vol. 13, No. 15.

  • 14.    Gailitis R. et al. Long-term properties of different fiber reinforcement effect on fly ash-based geopolymer composite / Crystals. 2021. Vol. 11, No. 7.

  • 15.    Lalit R., Mayank P., Ankur K. Natural fibers and biopolymers characterization: A future potential composite material / Strojnicky Casopis. 2018. Vol. 68, No. 1.

  • 16.    Kim N.K. et al. Fire-retardancy and mechanical performance of protein-based natural fibrebiopolymer composites / Composites Part C: Open Access. 2020. Vol. 1.

  • 17.    Bockstaller M.R. Progress in polymer hybrid materials / Progress in Polymer Science. 2015. Vol. 40, No. 1.

  • 18.    C. C. Chamis, R. F. Lark. Hybrid composites – state and art review: Analysis, Design, Application and Fabrication. 1977.

  • 19.    Zweben C. Tensile strength of hybrid composites // Journal of Materials Science. 1977. Vol. 12, No. 7.

  • 20.    Kouznetsova V.G., Geers M.G.D., Brekelmans W.A.M. Multi-scale second-order computational homogenization of multi-phase materials: A nested finite element solution strategy / Computer Methods in Applied Mechanics and Engineering. 2004.

  • 21.    Geers M.G.D., Kouznetsova V.G., Brekelmans W.A.M. Multi-scale computational homogenization: Trends and challenges / Journal of Computational and Applied Mathematics. 2010.

  • 22.    Li S. Boundary conditions for unit cells from periodic microstructures and their implications / Composites Science and Technology. 2008. Vol. 68, No. 9.

  • 23.    Korolev A., Vatin N. Elasticity modulus of cement composites predicting using layer structure model / Magazine of Civil Engineering. St. Petersburg Polytechnic University of Peter the Great, 2021. Vol. 104, No. 4. P. 10413.

  • 24.    Korolev A. et al. Polymers under load and heating deformability: Modelling and predicting // Polymers. 2021. Vol. 13, No. 3.

  • 25.    Katoueizadeh E., Zebarjad S.M., Janghorban K. A practical analytic model for predicting the performance of an encapsulated polymer composite / Applied Mathematical Modelling. 2020. Vol. 78.

  • 26.    Minh D.P.T., Khoa N.N. An analytic homogenization model in traction and bending for orthotropic composite plates with the type of double corrugated cardboard / Vietnam Journal of Mechanics. 2016. Vol. 38, No. 3.

  • 27.    Kim Y. et al. An extended analytic model for the elastic properties of platelet-staggered composites and its application to 3D printed structures / Composite Structures. 2018. Vol. 189.

  • 28.    Plecnik J.M., Gerwein P.H., Pham M.G. Design and construction of world’s tallest free-standing fiberglass stack / Civil engineering New York, N.Y. 1981.

  • 29.    Plecnik J.M. et al. Design concepts for the tallest free - standing fiberglass stack / Polymer Composites. 1984.

  • 30.    Ding A., Wang J., Ni A. The selection of safety factor of FRP chimney for coal-fired units / Fuhe Cailiao Xuebao/Acta Materiae Compositae Sinica. 2013.

  • 31.   O’Keefe W. Frp widens use in energy systems / Power. 1976.

  • 32.   Jackson K.R. Selection and design of chimneys and linings up to 80m high. 1976.

  • 33.    Honga S.J., Honga S.H., Doh J.M. Materials for flue gas desulfurization systems operating in Korea and their failures / Materials at High Temperatures. 2007.

  • 34.    Zhang D.H., Wang J.H. The FRP chimney design and construction technology for coal-fired power plant FGD system / Frontiers of Energy and Environmental Engineering - Proceedings of the 2012

• 35.    da Silva T.R. et al. Application of plastic wastes in construction materials: A review using the concept of life-cycle assessment in the context of recent research for future perspectives // Materials. 2021. Vol. 14, No. 13.

• 36.   GOST 19907–83 Dielectric fabrics made of glass. Twister complex threads. Specifications.

• 37.    National standard GOST RF 56810-2015 Polymer composites. Test method for flexural flat samples. 2017.

• 38.    A.V. Bezmelnicyn, S.B. Sapozhnikov. Multiscale modeling and formation analysis of technological interlaminar stresses in thick-walled gfrp rings // PNRPU Mechanics Bulletin. 2017. Vol. 2, No. 2.

• 39.    Bargmann S. et al. Generation of 3D representative volume elements for heterogeneous materials: A review / Progress in Materials Science. 2018. Vol. 96.

• 40.    Pelissou C. et al. Determination of the size of the representative volume element for random quasibrittle composites / International Journal of Solids and Structures. 2009. Vol. 46, No. 14–15.

• 41.    ANSYS. ANSYS Mechanical APDL Theory Reference // ANSYS Inc. 2013. Vol. Release15, No. November.

• 42.    Lisina S.A. Kontinualnye i strukturno-fenomenologicheskie modeli v mekhanike sred s mikrostrukturoj. Nizhnij Novgorod, 2009.

• 43.    Danilov M., Bardaev P. Structural-phenomenological stress-strain model for concrete / EPJ Web of Conferences. 2019. Vol. 221.

• 44.   Morozov I.A., Svistkov A.L. Structural-phenomenological model of the mechanical behavior of

  rubber / Composites: Mechanics, Computations, Applications. 2010. Vol. 1, No. 1.

International Conference on Frontiers of Energy and Environmental Engineering, ICFEEE 2012. 2013.