Прогнозирование временного ряда с учетом хаотической компоненты

Проблема моделирования и прогнозирования процессов, обладающих признаками детерминированного хаоса, весьма актуальна для многочисленных приложений [1, 2]. Особый интерес представляют подходы, позволяющие извлекать информацию из коротких временных рядов [3], так как существующие подходы к прогнозированию хаотических рядов (сингулярный спектральный анализ, нейронные сети, авторегрессионные модели) требовательны к длине ряда [4]. Работа продолжает исследования [5, 6].

• 2.    Разложение по хаотическому базису

Процесс у_к предлагается разложить по системе ортогональных функций [5]. Для х_к будем искать представление в виде линейной комбинации хаотических функций:

^хк =T,CL_ix_lk, k = \,N,                     (3)

/=1

где x_ik, i = l,m, к = 1,2,... образуют систему базисных функций, заданных в моменты времени к = 1,2,...; а, - весовые коэффициенты (константы) i = 1, т .

Задача сводится к выбору системы ортогональных функций x_ik, i = \,т:

N

1/_Cik^x_cjk=^ ^i*j                 (4)

и коэффициентов cc,, i = \,m по реализации y_k, k=\,N. В качестве базисных могут выступать функции, порождающие известные нелинейные отображения. В частности, это [5, 6] треугольные отображения

(2г х_к, 0<х„<1/2;

хк.А                                               --- (5)

\2rQ-xk\ 1/2<^<1; 1/2<г<1, А = 1,М логистические отображения хк+х = Ъск (1 - хк ), X] е (0; 1), X е (3,6; 4), к = 1, N, (6)

функция Вейерштрасса

W(a,b,t) = У^а" cos(bⁿnf).                 (7)

Я=1

Набор таких функций с определенными параметрами может образовать базис [8]. Процедура разложения ряда по базису хаотических функций осуществляется на основе последовательного выделения хаотических компонент. Для нахождения параметров модели (3) были предложены два алгоритма. Первый алгоритм основан на определении постоянных параметров X,, г,, a,, b,, i = l,m с помощью предварительно обученной на модельных данных трехслойной нейронной сети. Второй алгоритм заключается в определении параметров максимально коррелированных с рядом процессов из классов отображений, порожденных базисными функциями:

Pi = arg max с( у, x_t),                         (8)

где Pi - параметры функции, порождающей отображение xik, с - корреляционная функция. После нахождения базиса определяются константы а,:

N Г т

[а„...,а_т] = argmin£ ^-^а_ух_# ^а-            j=\

Исследования на модельных данных показали, что второй подход работоспособен при большем уровне шума (предельное отношение сигнал / шум -1 дБ).

• 3.    Модельный пример

• 4.    Пример прогнозирования ряда потребления электроэнергии

Рассмотренный подход применен к решению задачи прогнозирования модельного процесса у_к, к = 1,..., 20, порожденному суммой двух логистических отображений (с параметрами х₀₎ =0,6,

Х]=3,72, а]=0,65 и х02 =0,23, Х2 =3,81, ос2=О,3) и аддитивным белым гауссовым шумом Ek ~ N(0, 0,1), отношение сигнал / шум составило 3 дБ. Для сравнения приведен результат, полученный с помощью модели ARFIMA [9]:

dx_k=^Ly_k, de(0^.     (Ю)

На рис. 1 приведены аппроксимация, прогноз ряда у_к и сравнение результатов, полученных с помощью модели (3) и модели (10).

Ошибка аппроксимации по модели ARFIMA составила 8,8 %, по модели (3) - 4,5 %. Ошибка прогнозирования на 10 шагов вперед составила для модели ARFIMA 16,38 %, для модели (3) -5 %. При этом параметры логистических отображений найдены с погрешностью не более 1 %. Для сравнения, процедура, приведенная в [7], позволяет найти параметры логистических отображений при отношении сигнал/шум не менее 20 дБ.

Модель временного ряда потребления электроэнергии:

у_к=у‘_к+у⁵_к+§_к, к = 1Л,           (И)

где у_к - компонента тренда, у_к — сезонная компонента, §_к - остатки.

Подходы к прогнозированию компоненты тренда и сезонной компоненты рассмотрены в [8]. Остатки модели (11) рассматриваются как шум, случайные нормально распределенные величины ^ ~ А(0,<т2). Однако анализ остатков позволяет предположить, что ряд ^к является детерминированным хаосом. Индекс фрактальности для ряда ^к равен 0,67, что соответствует антиперси-

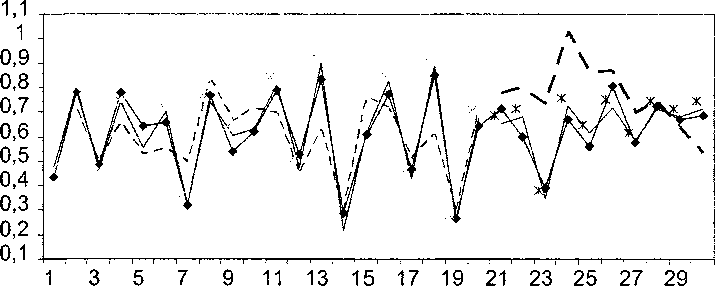
—♦— Исходный ряд у

----Аппроксимация (ARFIMA)

--Прогноз(АРР1МА)

—-‘—Аппроксимация по хаотической модели хг Прогноз по хаотической модели

Рис. 1. Аппроксимация и прогноз модельного ряда

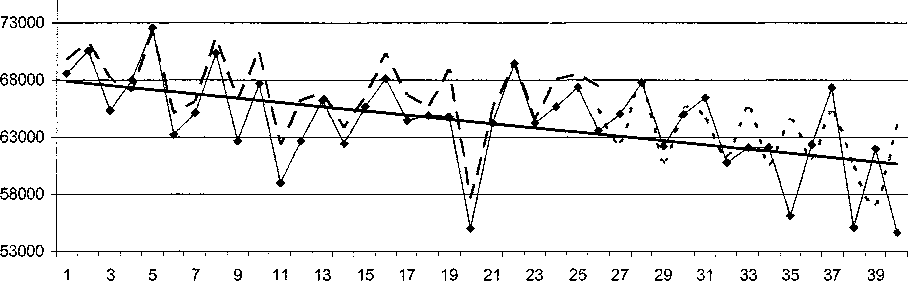
-*—Потребляемая электроэнергия, кВтч--Аппроксимация - - - -Прогноз------Тренд

Рис. 2. Аппроксимация и прогноз ряда потребления электроэнергии

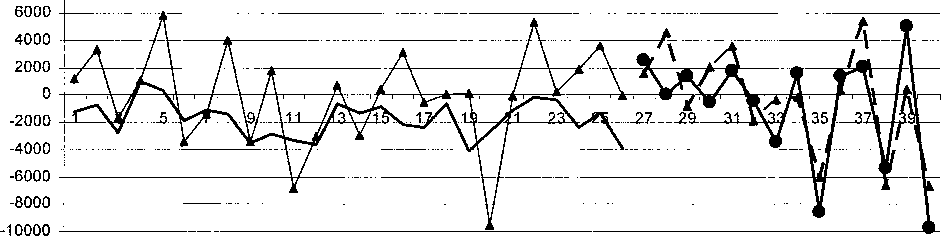
-----С хаотической составляющей: ошибка аппроксимации —•—ошибка прогнозирования

—*—Модель тренда: ошибка аппроксимации            —*— ошибка прогнозирования

Рис. 3. Сравнение ошибок аппроксимации и прогнозирования

стентному процессу (индекс фрактальности для белого шума равен 0,5).

Для построения прогноза ряда §_к построена модель вида (3) с количеством слагаемых т = 3 для к = 1,..., N . Прогноз ряда §_к с допустимой ошибкой не более 5 % может быть получен на 5 шагов вперед. Прогноз ^_к включается в модель (11) наряду с прогнозом у_к , у_к.

Включение в прогноз хаотической составляющей для данного ряда уменьшает среднюю ошибку прогноза на 5 шагов вперед с 16,5 % до 4,8 %, то есть в 4 раза. Результаты приведены на рис. 2, 3.

Заключение

Представленная процедура позволяет аппроксимировать хаотический временной ряд, разложив его на сумму антиперсистентных процессов. Важной особенностью решаемой задачи является малая длина выборки (N < 25). Полученные результаты могут найти применение для прогнозирования реальных хаотических процессов, повышения точности прогноза, а также в решениях задач фильтрации.