Прогнозная модель процесса флокуляции на основе нейронной сети

Регрессионный анализ, построение объясняющих регрессионных моделей при исследовании химико-технологических процессов считается дурным тоном. Подходом, заслуживающим одобрения, считается построение моделей на базе физических и химических законов – движения, сохранения, состояния и кинетики. Правда, при этом забывают, что многие устоявшиеся «законы», например, уравнения тепломассообмена и другие модели подобия, получены именно с помощью регрессионного анализа. Да и в уравнениях кинетики вида, например, dC ( t )/ dt = - к • C ( t ) n , где C ( t ) - зависимость концентрации от времени, n - порядок реакции, к - константа скорости реакции, являются регрессионно-дифференциальными уравнениями. Теоретически рассчитать k обычно невозможно, и ее определяют регрессионными методами по данным экспериментов.

В частности, при описании процесса флокуляции в составе практически важного и актуального сейчас для РФ производства калийных удобрений [1, 2] для описания зависимости количества частиц от времени N ( t ) используется уравнение Смолуховского dN ( t ) [dt = - к • N ( t ) ², константа k которого разными исследователями расшифровывается через параметры флокулянта, аппарата и условий протекания процесса. Действительно, с точки зрения академической науки важно получить всеобъемлющую математическую модель, обладающую широкой применимостью.

Однако на действующих производствах чаще встает задача оптимизации работы конкретного, существующего оборудования. Эта оптимизация возможна путем коррекции системы автоматического регулирования (САР), незначительных конструктивных изменений, небольших изменений параметров ведения процесса (заданий САР) и т. п. В любом варианте, потребуется математическая модель этого оборудования, свободными переменными которой будут параметры процесса, изменение которых возможно в данном конкретном случае. Казалось бы, регрессионные модели здесь вполне могут быть применены – но традиционный их базис в виде полиномов первой-второй степени не всегда позволяет производить условную оптимизацию, или получать асимптотические по времени значения (характерные, в частности, для процесса флокуляции), или даже вообще получать модели с малым среднеквадратичным рассогласованием с данными эксперимента.

Для получения моделей, пригодных для оптимизации производственных процессов в условиях единственного в России производителя калийных солей, в Березниковском филиале ФГБОУ ВО «Пермский национальный исследовательский университет» были проведены обширные экспериментальные исследования, описанные в [3]. В частности, с использованием датчика лазерного анализатора системы FBRM исследована динамика количества частиц (всех фракций) в объеме экспериментальной установки при кратном увеличении объема порции вносимого флокулянта.

Уравнение Смолуховского при N ( 0 ) = N ₀ имеет аналитическое решение N ( t ) =

N 0      ,

1 — к • N о • t

которое, как показали эксперименты, плохо аппроксимирует реальные данные (рис. 1).

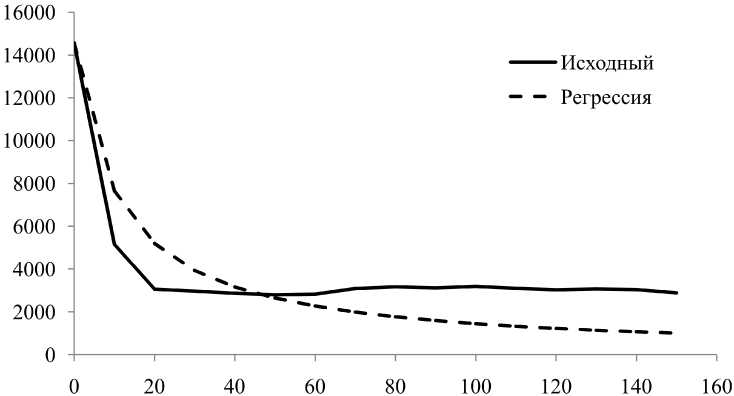
Рис. 1. Неудовлетворительный результат аппроксимации экспериментальных данных уравнением Смолуховского

Таким образом, ни классические регрессионные модели на основе полинома, ни широко распространенная и вроде бы физически обоснованная модель не позволяют получить достаточно качественную аппроксимацию экспериментальных данных, а значит, не могут быть использованы для оптимизации технологического процесса. Исследуем возможность применения других методов.

В некоторых случаях значительно более высокое качество аппроксимации и, тем более, про-

гнозов и постпрогнозов обеспечивают регрессионно-дифференциальные модели (РДМ) [4, 5].

Построение РДМ 2-го порядка, соответствующей задаче Коши

d ² N t dN t

---(^ = — b ---(Л + a . N ( t ) 2

²            dt

+ c ,

dN ( 0 )

dt

= N o ',

где a, b, c, N0 ' – неизвестные регрессионные коэффициенты, решает проблему низкого качества аппроксимации модели.

В то же время вопрос физической обусловленности коэффициентов последней модели представляется столь же неясным, сколь и для классической регрессионной задачи.

Существуют необъясняющие регрессионные методы, позволяющие строить модели с хорошей аппроксимацией и прогнозными свойствами. Это метод опорных векторов, прогнозные нейронные сети и т. д. Прогнозировать данные при помощи нейронных сетей можно только в том случае, когда существуют скрытые зависимости между входными и выходными данными. Тогда после обучения нейронная сеть может предсказать будущие значения на основе нескольких предыдущих значений и (или) каких-то существующих в настоящий момент факторов. Данная задача отвечает этим требованиям, поэтому на основе исходных данных можно обучить нейронную сеть и осуществить прогноз.

Информатика и вычислительная техника

Для обучения предложена нейронная сеть вида 2-10-10-10-1 и использованы 91 реальных измерений (табл. 1), произведенных при внесении в лабораторную установку разных объемов флокулянта q i , которые вошли в обучающую выборку (рис. 2).

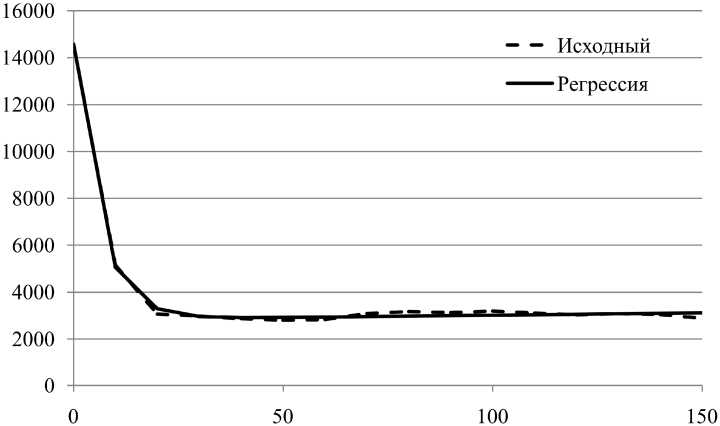
Рис. 2. Результат аппроксимации экспериментальных данных регрессионно-дифференциальным уравнением (1)

Таблица 1

Динамика количества частиц в объеме экспериментальной установки при кратном изменении объема порции флокулянта q_i = i · q ₁

t , c	q 1	q 2	q 3	q 4	q 5	q 6
0	14 574,2	17 035,8	16 479,4	15 581	13 869,2	14 228,4
10	5154,56	8347,33	13 091,7	7259,89	11 857,3	10 488,1
20	3058	5711,56	6179,67	4363,67	3861,78	4084,44
30	2971,22	5265,33	6127,22	4135,44	2687,67	2932,11
40	2865	5083,22	6025,22	3981	2427,89	2668
50	2796	5068,11	5790,78	3864	2379,56	2491,78
60	2829,22	5040,44	5613,22	3669,33	2174,22	2413,67
70	3084,56	4823,67	5726,67	3568	2143	2279,22
80	3170,67	4672	4700,56	3134,33	1921,44	2289,78
90	3121,44	4698,78	4548,78	3323,67	1714,22	2427,44
100	3187,44	4414,22	4351	3191,44	1717,89	2391
110	3102,89	4365,56	3995,56	2992,89	1692,78	2371
120	3029,44	4266,44	3932,22	2688,78	1672,89	2436,22
130	3072	4607,67	3947	2437,33	1740,78	2396,11
140	3035,11	4614,56	3959,44	2451,89	1614,67
150	2882,67	4522,11	4060,22		1627,44
160		4228,44	4095,78		1609
170		4289,22	3929,11
180		4096	3938,67
190		4004	3753,11
200		3989,44	3651,11

Для обучения нейронной сети необходимо выбрать подходящий алгоритм. Широко известным является алгоритм обратного распространения – итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойной нейронной сети и получения желаемого выхода. Несмотря на то, что общая идея этого метода состоит в распростране- нии сигналов ошибки от выходов сети к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы, существует несколько модификаций, отличающихся по скорости работы, частоте изменения весов и точности обучения.

Так, например, в алгоритме FANN_TRAIN_INCREMENTAL веса обновляются несколько раз в течение одной эпохи. За счет этого сеть обучается быстрее, но подходит для решения только простых задач. Алгоритм FANN_TRAIN_BATCH напротив, производит обновление весов всего один раз в течение эпохи после вычисления средней квадратичной ошибки для всей обучающей выборки. Это существенно повышает точность обучения, но требует больше времени по сравнению с предыдущим алгоритмом, за счет большего количества эпох для получения допустимой матрицы весовых коэффициентов [6].

Более продвинутой модификацией алгоритма обратного распространения является алгоритм FANN_TRAIN_RPROP. Он позволяет решить главный недостаток предыдущего алгоритма – скорость обучения. RPROP использует знаки частных производных для подстройки весовых коэффициентов. Для того чтобы определить величину коррекции используется правило:

A £ ) H

n ' ^A § ) ,

d E ⁽ t ) d E ⁽ t - 1)   _n

--> 0

П - A ( jt )

5 wij   5 wij dE(1) dE(1-1)

,

’ 9 w y   9 w j

< 0

где A w ^ ) = -n • -^ E- , A w j ) = -n • 8 ⁽ ” ) • y (ⁿ 1) . d w ij-

На каждом шаге по соответствующему весу wij рассчитывается производная, и, если она поменяла знак, это значит, что алгоритм «проскочил» локальный минимум. Необходимо сделать «откат», вернуть предыдущее значение весового коэффициент AWy (t) = AWy (t)-Ajt-1) и скор ректировать величину изменения на n- . Если знак частной производной не изменился, параметры обучения можно оставить такими же, однако для более быстрой сходимости можно увеличить величину коррекции на n+ [7].

Начальные значения для всех Aiy обычно устанавливаются равными 0,1. Для вычисления значения коррекции весов используется следующее правило:

( t ) ij ,

^A w y ( t ) = “

( t )

⁺ у ,

0,

5 E t l > 0 a w y

S-E1 < 0 a wy dE(t) _ 0 a wy

.

Если производная положительна, ошибка может увеличиваться, в этом случае нужно уменьшить весовой коэффициент, иначе – увеличить. Затем подстраиваются веса:

w y ( t ⁺ 1 ) = w y ( t ) ^{+ A} w y ( t ) .

Поэтому работа по данному алгоритму всегда начинается с определения начального значения величины коррекции A y . После обработки всей выборки и вычисления частных производных рассчитывается новое значение A y по формулам (1) и (3). Далее осуществляется корректировка весов по формуле (4) и проверяется условие остановки обучения нейронной сети. Если сеть признается необученной, то все этапы повторяются заново, начиная с предъявлений примеров обучающей выборки и расчета производных. Данный алгоритм сходится в 4–5 раз быстрее, чем стандартный алгоритм, поэтому для дальнейшей работы был выбран именно он [8].

Информатика и вычислительная техника

Далее необходимо выбрать активационную функцию нейронов. Наиболее распространенными являются линейная, пороговая, сигмоидальная и др.

При линейной передаточной функция сигнал на выходе нейрона линейно связан со взвешенной суммой сигналов на его входе:

f (x ) = tx, где t – параметр функции. Одной из модификаций линейной функции является полулинейная функция или шаговая, которую можно представить формулой

0, при x <  0

f ( x ) = П при x >  1

.

x , при 0 <  x <  1

Пороговая передаточная функция всегда принимает значения только 0 или 1 и графически представляет собой перепад. Пока сигнал на входе нейрона будет меньше значения T – сигнал на выходе будет равен 0. Если же сигнал на входе достиг заданного порога или превысил его – выходной сигнал скачкообразно изменится на единицу. Математически функцию можно описать так:

x J 1, при x >  T f ( ^x ) =L        ,

.

[ 0, при x <  T

Пороговая функция наиболее часто применима при обучении персептронов, однако в сетях, использующих в качестве обучения алгоритм обратного распространения ошибки, использоваться не может, так как данная функция не является дифференцируемой на всей оси абсцисс.

Наиболее часто используемой функцией активации является сигмоидальная передаточная функция. Сигмоидальный тип был введен для того, чтобы перейти от бинарных значений пороговых функций, выходы которых принимают значения либо 0, либо 1, к аналоговым. Это позволило применять нейронные сети в более широком круге задач, а не только в задачах классификации. Область значений данной функции находится в интервале (0, 1).

Функцию математически можно выразить как

° ( x ) =

1 + exp ( - tx ) ’

где t – это параметр функции, который определяет ее крутизну. Сигмоида может принимать вид пороговой функции при t ^ да . При t = 0 сигмоидальная передаточная функция вырождается в постоянную функцию со значением 0,5. Производная выглядит следующим образом:

^ ^ ^xx ) = ^{tf ( x )( 1 -} f ^{( x} )\

Простота производной, а также тот факт, что она может быть выражена через значение функции, является важным достоинством сигмоиды и облегчает применение алгоритма обратного распространения при обучении нейронной сети. Еще одной особенностью данной активационной функции является различное изменение сигналов в зависимости от их значений. Так, более сильные сигналы усиливаются значительно меньше, чем слабые, что позволяет предотвратить насыщение от больших сигналов.

К сигмоидальному типу также относится функция гиперболического тангенса

, x exp ( Ax ) - exp ( - Ax )

th ( Ax ) =----7 ;-------7-----7 , exp (Ax) + exp (- Ax)

которая отличается от рассмотренной выше кривой тем, что его область значений лежит в интервале (–1; 1).

Перечисленные выше функции составляют лишь часть от множества передаточных функций, используемых на данный момент. В число других передаточных функций входят такие как: экспонента f ( x ) = exp ( - Ax ) ; тригонометрический синус; модульная: f ( x ) = | x |; квадратичная [9].

Исходя из имеющихся данных, была выбрана гомогенная структура нейронной сети с сигмоидальной активационной функцией FANN_SIGMOID.

В итоге, нейронная сеть включает в себя входной и выходной слой, в соответствии с количеством входов и выходов обучающей выборки и 3 скрытых слоя. Настройки нейронной сети подбирались экспериментально. Скорость обучения сети составила 0,7, количество эпох изменялось от 1000 до 30 000.

Для оценки точности обучения и допустимости использования сети в дальнейшем для прогнозирования была использована тестовая выборка (табл. 2), полученная в ходе эксперимента с q 6 = 6· q 1 .

Для начального значения 1000 эпох значения обучающей выборки получились следующие: максимальное отклонение max S оВ = 1,402, минимальное отклонение min S оВ = 0,02, среднеквадратичное отклонение 5 оВ = 0,394. Значения для тестовой выборки соответственно max S ТВ = 0,492, min S ТВ = 0,026 и 5 _ТВ = 0,237 (табл. 3).

Таблица 2

Тестовая выборка

X 1	Y ТВ
0	14 228,4
10	10 488,1
20	4084,44
30	2932,11
40	2668
50	2491,78
60	2413,67
70	2279,22
80	2289,78
90	2427,44
100	2391
110	2371
120	2436,22
130	2396,11

Таблица 3

Расчет отклонений тестовой выборки

X 1	X 2	Y ТВ	Y НС	S
0	0,6	14 228,4	7374,818	0,481683
10	0,6	10 488,1	5327,791	0,492016
20	0,6	4084,44	4190,437	–0,02595
30	0,6	2932,11	3582,162	–0,2217
40	0,6	2668	3244,828	–0,2162
50	0,6	2491,78	3047,881	–0,22317
60	0,6	2413,67	2927,394	–0,21284
70	0,6	2279,22	2850,803	–0,25078
80	0,6	2289,78	2800,58	–0,22308
90	0,6	2427,44	2766,787	–0,1398
100	0,6	2391	2743,535	–0,14744
110	0,6	2371	2727,216	–0,15024
120	0,6	2436,22	2715,55	–0,11466
130	0,6	2396,11	2707,066	–0,12978

Проведя несколько экспериментов, изменяя количество эпох обучения, получили следующие значения (табл. 4, рис. 3).

Таблица 4

Зависимость отклонений тестовой выборки от количества эпох обучения

Количество эпох		Максимальное отклонение	Минимальное отклонение	Среднеквадратичное отклонение
Обучающая выборка	1000	1,401691	0,019681	0,393720
	2000	2,044962	0,000331	0,386935
	3000	4,243325	0,003226	0,566561
	5000	0,293571	0,009317	0,121480
	10 000	0,060327	0,000273	0,020420
	15 000	0,148558	0,000174	0,050049
	20 000	0,177938	0,001109	0,049944
	30 000	0,072878	0,000043	0,026951
Тестовая выборка	1000	0,492016	0,025952	0,237345
	2000	0,567789	0,029189	0,193696
	3000	0,479123	0,005286	0,186921
	5000	0,628138	0,043784	0,211856
	10 000	0,318403	0,056411	0,146638
	15 000	0,339127	0,093880	0,109175
	20 000	0,236722	0,016275	0,107552
	30 000	0,264045	0,065096	0,064052

Информатика и вычислительная техника

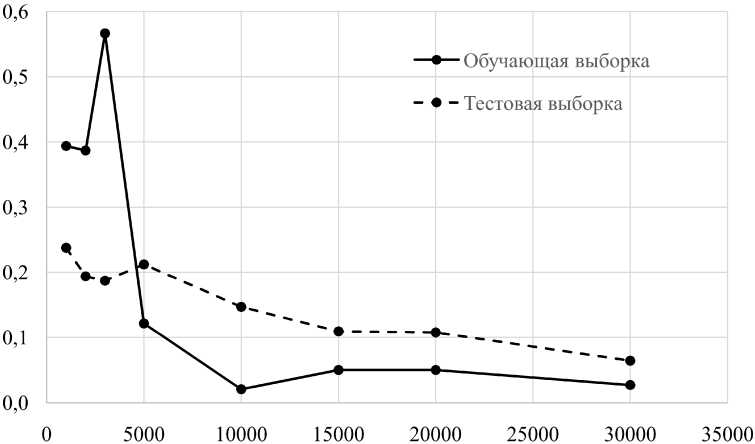
Рис. 3. Зависимость среднеквадратичного отклонения от количества эпох обучения

Как видно из рис. 3, достаточным количеством является 15 000 эпох обучения, при котором среднеквадратичное отклонение в обучающей и тестовой выборках составило 5 и 11 % соответственно. Меньшее количество эпох дает недопустимо большую погрешность, а увеличение количества эпох ведет к существенному замедлению обучения, а также может привести к переобучению нейронной сети.

Также было обнаружено, что максимальные значения погрешности достигаются при значениях 10 и 20 с. Эта тенденция сохраняется даже при выборе оптимального количества эпох обучения. Это обусловлено большим разбросом значений на этом интервале, что мешает нейронной сети выявить закономерность (рис. 4).

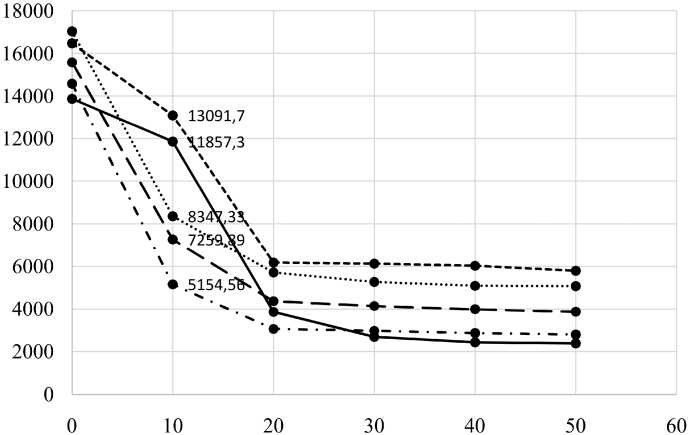
Рис. 4. Зависимость погрешности определения количества частиц в разных выборках от модельного времени, с

Возможно, эту проблему удалось бы решить за счет большего количества данных в обучающей выборке. Также это позволило бы уменьшить количество эпох, а значит сократить время на обучение нейронной сети.

Тем не менее, полученный результат дает значительно лучшее качество аппроксимации исходных данных и позволяет прогнозировать развитие процесса флокуляции при произвольном размере порции флокулянта, чем традиционные регрессионные модели или модель Смолуховского.