Прогнозная оценка численности населения самарской области на основе экономико-математического моделирования

Одним из методов прогнозирования, получивших наибольшее распространение, является экономико-математическое моделирование, которое и будет основной для расчетов в данной статье.

Понятие «численности населения», пожалуй, является одним из основополагающих показателей развития человечества, так как отражает его количественную характеристику. Стоит заметить, что на протяжении многих веков об этом никто всерьёз не задумывался; люди просто жили на родной им земле и мало-помалу осваивали всё новые и новые территории. Однако в последнее тысячелетие произошёл огромный скачок роста численности населения (примерно в 25 раз). Сейчас на планете проживает более 7 млрд. человек, и если в Европе численность населения достигла своего пика к концу прошлого века, то в развивающихся странах прирост населения каждый год увеличивается.

Что касается России, то здесь всё не так однозначно: с одной стороны, 146 млн. человек для такой большой по площади страны – это достаточно мало; с другой стороны, если учитывать, что большую часть страны составляют районы севера с весьма суровым климатом, сосредоточение 70% населения на европейской части России становится вполне логичным [1].

Если наиболее подробно рассматривать Самарскую область, как одного из наиболее типичных представителей упомянутой выше европейской части страны, необходимо прибегнуть к анализу статистической информации. Данные об основных характеристиках (к коим относится и численность населения) можно найти на официальном сайте Федеральной службы государственной статистики в разделе публикаций «Регионы России». В табл. 1 представлены данные о численности населения Самарской области за одиннадцать лет, рассчитаны абсолютный прирост, темп роста, темп прироста и абсолютное значение 1% прироста, что позволяет объективно оценить сложившуюся ситуацию.

Таблица 1

Численность населения Самарской области за 2003-2013 гг.

Год	Числ-ть населен ия, тыс. чел.	Абсолютный прирост, тыс. чел.		Темп роста, %		Темп прироста, %		Абс. значе ние 1% прир оста
		цепной	базисны й	цепной	базисны й	цепно й	базисны й
2004	3229,20
2005	3225,30	-3,90	-3,90	99,88	99,88	-0,12	-0,12	32,29
2006	3225,60	0,30	-3,60	100,01	99,89	0,01	-0,11	32,25
2007	3224,00	-1,60	-5,20	99,95	99,84	-0,05	-0,16	32,26
2008	3220,90	-3,10	-8,30	99,90	99,74	-0,10	-0,26	32,24
2009	3221,50	0,60	-7,70	100,02	99,76	0,02	-0,24	32,21
2010	3220,90	-0,60	-8,30	99,98	99,74	-0,02	-0,26	32,21
2011	3215,30	-5,60	-13,90	99,83	99,57	-0,17	-0,43	32,21
2012	3214,10	-1,20	-15,10	99,96	99,53	-0,04	-0,47	32,15
2013	3213,30	-0,80	-15,90	99,98	99,51	-0,02	-0,49	32,14
2014	3211,20	-2,10	-18,00	99,93	99,44	-0,07	-0,56	32,13

По анализу данных таблицы можно сделать вывод о том, что численность населения Самарской области за указанный период в основном имела отрицательную динамику.

Численность населения – один из наиболее значимых показателей развития региона, поэтому необходимо выяснить, как он будет изменяться в будущем, какие факторы на него могут влиять, и на основе полученной информации скорректировать будущие изменения. В качестве показателей, оказывающих влияние на численность населения Самарской области, были выбраны рождаемость и смертность населения с 2004 по 2014 годы [3]. Данные показатели отражены в таблице 2.

Таблица 2

Число родившихся и умерших на 1000 человек населения в Самарской области за 2003-2013 годы

Год	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014
Родившихся, чел.	9,8	10,1	9,7	10,1	10,7	11,4	11,5	11,6	11,5	12,1	12,3
Умерших, чел.	16,4	16,2	16,1	15,7	15,3	15,3	14,8	15,2	14,4	13,9	14,3

Анализ данных таблицы позволяет сделать вывод о том, что смертность в Самарской области в каждом году исследуемого периода выше, чем рождаемость. Данный факт имеет явно негативный характер, однако, по утверждению демографов, разрыв между смертностью и рождаемостью для данной области и для страны в целом в большей мере обусловлен низкой рождаемостью, чем высокой смертностью. Также можно отметить, что с каждым годом рождаемость увеличивается, а уровень смертности снижается, хоть и перекрывает рождаемость даже в отчетном году.

Предварительная обработка динамического ряда состоит в сглаживании ряда. Для точности и наглядности построения графика необходимо произвести сглаживание по пяти точкам, которое далее отображено в таблице 3.

Таблица 3

Сглаживание показателя по пяти точкам

Показате ль	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014
Населен ие Самарск ой области, тыс. чел.	3228, 6	3226, 8	3225, 0	3223, 5	3222, 6	3220, 5	3218, 5	3217, 0	3215, 0	3212, 8	3210, 7

Для определения наличия тренда временного ряда используется метод проверки разностей средних уровней. Динамический ряд разбивается на 2 примерно равные части и по каждой части находятся средние значения и исправленная дисперсия [2]. Данные расчеты отразим в табл. 4.

Таблица 4

Результаты расчетов средних значений показателей динамического ряда и исправленных дисперсий

Первая часть ряда (2004-2009)		Вторая часть ряда (20010-2014)
Среднее значение, ПЭ1	Исправленная дисперсия, S 2	Среднее значение, ПЭ2	Исправленная дисперсия,
3224,5	8,59	3214,8	9,85

После этих расчетов проверяется гипотеза о равенстве дисперсий двух совокупностей на основе F-критерия Фишера-Снедекора. Расчетное значение сравнивается с табличным критическим при уровне погрешности 5% и степенями свободы k1=5 и k2=4. Fрасч < Fтабл, следовательно, расхождение между дисперсиями случайно, то есть тренд существует. Проверяется окончательная гипотеза о наличии, которая производится с использованием t-критерия Стьюдента.

Расчетное значение t-критерия сравнивается с табличным при уровне значимости (а<0,05) и степенями свободы к = П 1 + п₂ — 2 . tpac4 > tтабл, следовательно, тренд существует. Расчетные значения обозначенных критериев представлены ниже в таблице 5.

Таблица 5

Расчетные значения критериев Фишера-Снедекора и Стьюдента

Критерий Фишера-Снедекора		Критерий Стьюдента
Fрасч	Fтабл	tрасч	tтабл
1,15	6,26	2,49	2,26

Модель выражается уравнением с определенной зависимостью между параметрами. Выявление характера такой зависимости возможно с помощью визуального метода.

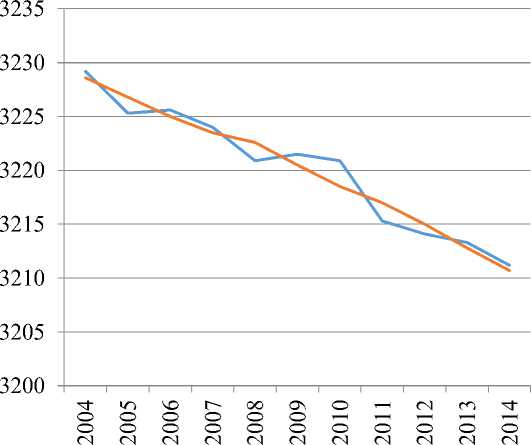
Исходный график

Сглаживание по 5 точкам

Рис.1. Динамика показателей численности населения Самарской области, тыс.чел.

Определение типа зависимости и расчет первых средних приростов:

Ut2=-1,8; Ut3=-1,65; Ut4=-1,2; Ut5=-1,5; Ut6=-2,05; Ut7=-1,75; Ut8=-1,75; Ut9=-2,1; Ut10=-2,15. Вычисленные значения примерно одинаковы, что подтверждает правильность вывода о линейной зависимости. Уравнение зависимости примет вид:

ЧН — a0 + a1t + a2x + a3z,                            (1)

где ЧН – численность населения по Самарской области;

• x – рождаемость в Самарской области;

• z – смертность в Самарской области;

a0, a1, a2, a3 – неизвестные параметры;

• t – вбирает в себя все неучтенные факторы и характеризуется как

время.

Неизвестные параметры a0,  a1,  a2, a3 вычисляются наименьших квадратов посредством системы линейных уравнений:

(£ ЧН — na0 + a1£t + a2£x + a3£z £ ЧН * t = a0 £ t + a1 £ t2 + a2 £ xt + a3 £ zt £ЧН * x — ao £ x + a^ £ x t + a2 £ x + a3 £ zx £ЧН * z = a0£ z + a1£ zt + a2£ zx + a3£ z2

35421=11a0+66a1+120,8a2+167,6a3

212333,4=66a0+506a1+754,5a2+979,3a3

388935,27=120,8a0+754,5a1+1335,36a2+1833,41a3

539733,21=167,6a0+979,3a1+1833,41a2+2560,42a3

методом

a0 =3228,88 a1=-1,88 a2= 0,39

a3=-0,11

Искомое уравнение зависимости примет следующий вид:

ЧН=3228,88-1,88t+0,39x-0,11z.                (3)

Произведем расчет средней относительной ошибки по формуле:

m = 1^1^*100                         (4)

m=0,04 - значение ошибки мало, что позволяет судить о надежности модели.

При прогнозировании численности населения Самарской области на 2015 и 2016 годы, предполагая, что рождаемость и смертность в 2015 будут составлять 12,92 и 13,62 чел. на 1000 человек населения соответственно, а в 2016 году 13,57 и 12,97 чел. соответственно, получаем в 2015 прогнозируемую численность населения в Самарской области 3209,86 тыс.чел., а в 2016 году 3208,31 тыс. чел.

Таким образом, малая величина ошибки в отклонениях между практическими и теоретическими значениями критериальной переменной свидетельствует о надежности найденной закономерности и возможности ее использования для решения практических задач.