Прогнозные математические модели качества печатных узлов космической аппаратуры

Автор: Шумских И.Ю., Тюлевин С.В., Пиганов М.Н.

Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc

Рубрика: Достижения физики, электроники и нанотехнологий

Статья в выпуске: 4-4 т.13, 2011 года.

Бесплатный доступ

Приведены результаты построения прогнозных моделей качества паяных соединений печатных узлов на основе припойных паст Indium. Для построения моделей были использованы регрессионный и программный комплекс «Прогнозирование 1.3». Рассмотрены три приема преобразования результатов обучающего эксперимента: нормирование и центрирование контролируемых параметров, нормирование по математическому ожиданию, нормирование по дисперсии. Проведено исследование и дана сравнительная оценка математических моделей.

Математическая модель, прогноз, паяные соединения, печатный узел, регрессия, обучение, эффективность прогнозирования

Короткий адрес: https://sciup.org/148200264

IDR: 148200264

Текст научной статьи Прогнозные математические модели качества печатных узлов космической аппаратуры

паяные соединения, печатный узел, регрессия, обу-

Одним из перспективных направлений в разработке эффективных и экономически приемлемых методов оценки качества и надежности РЭС и ЭРИ является индивидуальное прогнозирование их будущего состояния [1-5]. Наименьшие затраты времени при индивидуальном прогнозировании обеспечивают методы теории распознавания образов [3]. Если число информативных параметров превышает два, то целесообразно использовать метод регрессионных моделей (регрессионный метод) [6].

Методика построения моделей. Индивидуальное прогнозирование с использованием методов теории распознавания образов включает следующие основные этапы: обучающий эксперимент, обучение, экзамен и собственно прогнозирование. Процедура обучающего эксперимента для паяных соединений (ПС) на основе припой-ных паст Indium NC-SMQ92J рассмотрена в предыдущей работе. В ней для прогнозирования качества ПС было рекомендовано три информативных параметра: вязкость (Х1), клейкость (Х2) и кислотное число (Х3). Для построения прогнозных моделей проведем обучение и экзамен. Выберем регрессионный метод, т.к. число информативных параметров больше двух. В качестве прогнозируемого параметра будем использовать поверхностное сопротивление изоляции (Y).

Обучение заключалось в обработке результатов обучающего эксперимента в соответствии с выбранным оператором прогнозирования. Теоретические основы и математический аппарат для данного этапа описаны в [7]. Построение моделей проводилось с использованием программного комплекса «Прогнозирование 1.3» [8]. В процессе обработки результатов обучающего эксперимента

Таблица 1. Результаты обучающего эксперимента

Класс годности	Поверхностное сопротивление изоляции,10⁹Ом	Вязкость, Па∙с	Клейкость, г	Кислотное число, мг КОН
1	2,8	195	39	112
2	0,8	201	41	108
2	0,7	205	43	106
2	0,5	211	45	101
1	2,9	190	38	112
1	2,2	199	39	111
1	3,5	181	36	112
2	0,9	204	41	110
1	3,3	176	35	113
1	3,0	179	36	112
2	0,5	208	42	100
1	3,3	159	32	114
1	2,4	164	34	113
1	3,8	185	37	112
2	0,9	202	40	109
1	2,9	195	39	111
2	0,8	204	43	107
1	3,7	190	38	112
1	4,0	191	38	112
2	0,6	206	45	105
1	4,2	186	37	112
1	3,8	183	37	112
2	0,9	204	41	110
2	0,7	206	43	107
1	3,5	180	36	113
2	0,5	211	45	102
1	3,2	191	38	112
1	3,8	175	35	113
2	0,8	202	42	108
1	3,9	178	35	113
2	0,7	204	43	106
1	3,2	190	36	113
1	2,5	194	37	112
2	0,8	204	42	107
1	3,2	187	36	113
1	2,6	179	35	113
2	0,5	211	45	100
1	3,0	169	35	113
1	3,2	185	36	113
1	3,6	192	37	112
2	0,8	207	43	107
1	3,1	184	36	113
2	0,8	201	41	108
1	3,5	193	37	113
1	2,8	168	35	113
1	3,5	187	36	112
2	0,9	200	40	109
1	2,9	192	37	112
2	0,5	212	46	101
2	0,7	205	44	106

Таблица 2. Преобразованные данные по нормировке и центрированию

№ Y X1 X2 X3 Y Y* dY 1 0,4332 0,1891 0,0169 0,5669 2,8 2,4456 0,3544 2 -1,0921 0,6429 0,5806 -0,4638 0,8 1,6123 -0,8123 2 -1,1684 0,9455 1,1443 -0,9792 0,7 0,9310 -0,2310 2 -1,3209 1,3993 1,7080 -2,2675 0,5 0,0082 0,4919 1 0,5094 -0,1891 -0,2649 0,5669 2,9 2,6566 0,2434 1 -0,0244 0,4917 0,0169 0,3092 2,2 2,4099 -0,2099 1 0,9670 -0,8699 -0,8286 0,5669 3,5 3,0919 0,4081 2 -1,0158 0,8699 0,5806 0,0515 0,9 1,8314 -0,9314 1 0,8145 -1,2481 -1,1105 0,8246 3,3 3,3923 -0,0923 1 0,5857 -1,0211 -0,8286 0,5669 3 3,0651 -0,0651 2 -1,3209 1,1724 0,8625 -2,5252 0,5 0,7126 -0,2126 1 0,8145 -2,5339 -1,9560 1,0822 3,3 4,0878 -0,7878 1 0,1281 -2,1557 -1,3923 0,8246 2,4 3,5094 -1,1094 1 1,1958 -0,5673 -0,5468 0,5669 3,8 2,8676 0,9324 2 -1,0158 0,7186 0,2988 -0,2061 0,9 1,9932 -1,0932 1 0,5094 0,1891 0,0169 0,3092 2,9 2,3562 0,5438 2 -1,0921 0,8699 1,1443 -0,7215 0,8 1,0070 -0,2070 1 1,1196 -0,1891 -0,2649 0,5669 3,7 2,6566 1,0434 1 1,3483 -0,1135 -0,2649 0,5669 4 2,6700 1,3300 2 -1,2446 1,0211 1,7080 -1,2368 0,6 0,2988 0,3012 1 1,5009 -0,4917 -0,5468 0,5669 4,2 2,8810 1,3190 1 1,1958 -0,7186 -0,5468 0,5669 3,8 2,8407 0,9593 2 -1,0158 0,8699 0,5806 0,0515 0,9 1,8314 -0,9314 2 -1,1684 1,0211 1,1443 -0,7215 0,7 1,0338 -0,3338 1 0,9670 -0,9455 -0,8286 0,8246 3,5 3,1680 0,3320 2 -1,3209 1,3993 1,7080 -2,0099 0,5 0,0976 0,4024 1 0,7382 -0,1135 -0,2649 0,5669 3,2 2,6700 0,5300 1 1,1958 -1,3237 -1,1105 0,8246 3,8 3,3789 0,4211 2 -1,0921 0,7186 0,8625 -0,4638 0,8 1,3476 -0,5476 1 1,2721 -1,0968 -1,1105 0,8246 3,9 3,4192 0,4808 2 -1,1684 0,8699 1,1443 -0,9792 0,7 0,9175 -0,2175 1 0,7382 -0,1891 -0,8286 0,8246 3,2 3,3021 -0,1021 1 0,2044 0,1135 -0,5468 0,5669 2,5 2,9883 -0,4883 2 -1,0921 0,8699 0,8625 -0,7215 0,8 1,2850 -0,4850 1 0,7382 -0,4160 -0,8286 0,8246 3,2 3,2619 -0,0619 1 0,2807 -1,0211 -1,1105 0,8246 2,6 3,4326 -0,8326 2 -1,3209 1,3993 1,7080 -2,5252 0,5 -0,0813 0,5813 1 0,5857 -1,7775 -1,1105 0,8246 3 3,2984 -0,2984 1 0,7382 -0,5673 -0,8286 0,8246 3,2 3,2351 -0,0351 1 1,0433 -0,0378 -0,5468 0,5669 3,6 2,9615 0,6385 2 -1,0921 1,0968 1,1443 -0,7215 0,8 1,0472 -0,2472 1 0,6620 -0,6429 -0,8286 0,8246 3,1 3,2216 -0,1216 2 -1,0921 0,6429 0,5806 -0,4638 0,8 1,6123 -0,8123 1 0,9670 0,0378 -0,5468 0,8246 3,5 3,0643 0,4357 1 0,4332 -1,8532 -1,1105 0,8246 2,8 3,2850 -0,4850 1 0,9670 -0,4160 -0,8286 0,5669 3,5 3,1724 0,3276 2 -1,0158 0,5673 0,2988 -0,2061 0,9 1,9663 -1,0663 1 0,5094 -0,0378 -0,5468 0,5669 2,9 2,9615 -0,0615 2 -1,3209 1,4750 1,9899 -2,2675 0,5 -0,2565 0,7565 2 -1,1684 0,9455 1,4262 -0,9792 0,7 0,6529 0,0471 MO: -7,11E-17 -1,55E-17 6,17E-16 7,11E-16 2,232 2,232 5,53E-16 DIS: 1 1 1 1 1,7194 1,3229 0,3965 SKO: 1 1 1 1 1,3112 1,1502 0,6297 был сделан переход от оперирования со значениями информативных параметров к разностям этих значений и проведено нормирование и центрирование контролируемых информативных параметров, а также нормирование по математическому ожиданию и дисперсии. При установлении

граничного значения прогнозируемого параметра поверхностное сопротивление изоляции, равного 1∙109 Ом, выявлен фактический класс годности каждого экземпляра: годные – 1, не годные – 2 (табл. 1). В табл. 2 представлены преобразованные данные по нормировке и центрированию.

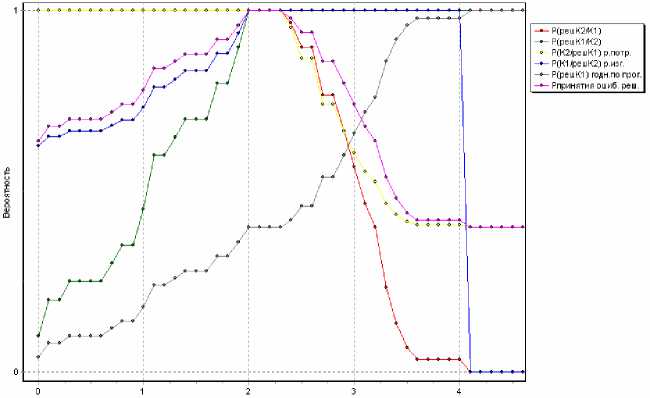
На рис. 1 приведена зависимость вероятностных характеристик от порога регрессионной функции П для первого приема преобразования данных. Из рисунка видно, что при П>4,1 риск изготовителя равен нулю. Минимальное значение риска потребителя равно 0,39 при П=4,1-4,7. Минимальное значение вероятности ошибки составляет 0,39 при П=4,15-4,7. В табл. 3 представлены преобразованные данные по нормировке математического ожидания (МО) признаков.

Порог параметра, П

Рис. 1. Влияние порога регрессионной функции на эффективность прогнозной модели при нормировке и центрировании

Таблица 3. Преобразованные данные по нормировке МО

№	Y	X1	X2	X3	Y	Y*	dY
1	2	3	4	5	6	7	8
1	1,2545	1,0130	1,0015	1,0200	2,8	5,8415	-3,0415
2	0,3584	1,0442	1,0529	0,9836	0,8	-3,2387	4,0387
2	0,3136	1,0649	1,1043	0,9654	0,7	-9,4236	10,1236
2	0,2240	1,0961	1,1556	0,9199	0,5	-20,0643	20,5643
1	1,2993	0,9870	0,9759	1,0200	2,9	7,0352	-4,1352
1	0,9857	1,0338	1,0015	1,0109	2,2	4,7323	-2,5323
1	1,5681	0,9403	0,9245	1,0200	3,5	9,5352	-6,0352
2	0,4032	1,0597	1,0529	1,0018	0,9	0,2206	0,6794
1	1,4785	0,9143	0,8988	1,0291	3,3	12,2893	-8,9893
1	1,3441	0,9299	0,9245	1,0200	3	9,3096	-6,3096
2	0,2240	1,0805	1,0786	0,9108	0,5	-16,6903	17,1903
1	1,4785	0,8260	0,8218	1,0383	3,3	17,2050	-13,9050
1	1,0753	0,8520	0,8731	1,0291	2,4	12,6933	-10,2933
1	1,7025	0,9610	0,9502	1,0200	3,8	8,2288	-4,4288
2	0,4032	1,0494	1,0272	0,9927	0,9	0,1921	0,7079
1	1,2993	1,0130	1,0015	1,0109	2,9	4,2811	-1,3811
2	0,3584	1,0597	1,1043	0,9745	0,8	-7,9760	8,7760
1	1,6577	0,9870	0,9759	1,0200	3,7	7,0352	-3,3352
1	1,7921	0,9922	0,9759	1,0200	4	7,1479	-3,1479
2	0,2688	1,0701	1,1556	0,9563	0,6	-14,3865	14,9865
1	1,8817	0,9662	0,9502	1,0200	4,2	8,3416	-4,1416
1	1,7025	0,9507	0,9502	1,0200	3,8	8,0032	-4,2032
2	0,4032	1,0597	1,0529	1,0018	0,9	0,2206	0,6794
2	0,3136	1,0701	1,1043	0,9745	0,7	-7,7504	8,4504
1	1,5681	0,9351	0,9245	1,0291	3,5	10,9829	-7,4829
2	0,2240	1,0961	1,1556	0,9290	0,5	-18,5039	19,0039
1	1,4337	0,9922	0,9759	1,0200	3,2	7,1479	-3,9479
1	1,7025	0,9091	0,8988	1,0291	3,8	12,1765	-8,3765
2	0,3584	1,0494	1,0786	0,9836	0,8	-4,8835	5,6835
1	1,7473	0,9247	0,8988	1,0291	3,9	12,5149	-8,6149
2	0,3136	1,0597	1,1043	0,9654	0,7	-9,5364	10,2364
1	1,4337	0,9870	0,9245	1,0291	3,2	12,1108	-8,9108
1	1,1201	1,0078	0,9502	1,0200	2,5	9,2439	-6,7439
2	0,3584	1,0597	1,0786	0,9745	0,8	-6,2184	7,0184
1	1,4337	0,9714	0,9245	1,0291	3,2	11,7724	-8,5724
1	1,1649	0,9299	0,8988	1,0291	2,6	12,6277	-10,0277
2	0,2240	1,0961	1,1556	0,9108	0,5	-21,6248	22,1248
1	1,3441	0,8779	0,8988	1,0291	3	11,4997	-8,4997
1	1,4337	0,9610	0,9245	1,0291	3,2	11,5468	-8,3468
1	1,6129	0,9974	0,9502	1,0200	3,6	9,0184	-5,4184

Продолжение таблицы 3
1	2	3	4	5	6	7	8
2	0,3584	1,0753	1,1043	0,9745	0,8	-7,6376	8,4376
1	1,3889	0,9558	0,9245	1,0291	3,1	11,4340	-8,3340
2	0,3584	1,0442	1,0529	0,9836	0,8	-3,2387	4,0387
1	1,5681	1,0026	0,9502	1,0291	3,5	10,6916	-7,1916
1	1,2545	0,8727	0,8988	1,0291	2,8	11,3869	-8,5869
1	1,5681	0,9714	0,9245	1,0200	3,5	10,2120	-6,7120
2	0,4032	1,0390	1,0272	0,9927	0,9	-0,0335	0,9335
1	1,2993	0,9974	0,9502	1,0200	2,9	9,0184	-6,1184
2	0,2240	1,1013	1,1813	0,9199	0,5	-21,7091	22,2091
2	0,3136	1,0649	1,1299	0,9654	0,7	-11,1812	11,8812
MO:	1	1	1	1	2,232	2,232	1,07E-15
DIS:	0,3451	0,0047	0,0083	0,0012	1,7194	114,6280	91,8665
SKO:	0,5875	0,0687	0,0911	0,0353	1,3112	10,7064	9,5847

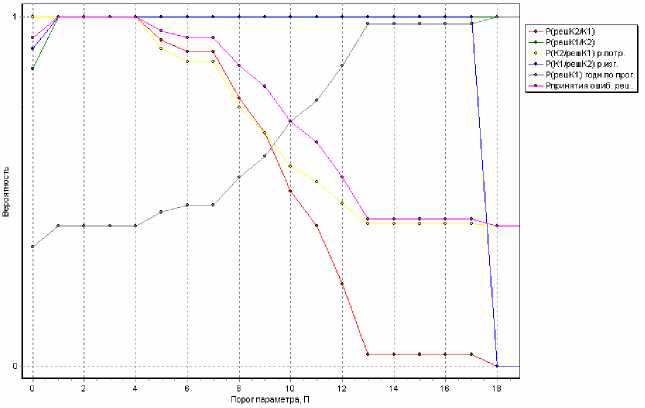
Рис. 2. Влияние порога регрессионной функции на эффективность прогнозной модели при нормировке

На рис. 2 приведена аналогичная зависи- при П=18-20, а риск изготовителя равен нулю при мость для второго приема преобразования данных. П>18. Вероятность ошибки при П=18-20 равна Как видно из данного рисунка минимальное значе- 0,39. В табл. 4 представлены преобразованные ние риска потребителя также равно 0,39, но уже данные по нормировке дисперсии признаков.

Таблица 4. Преобразованные данные по нормировке дисперсии

№	Y	X1	X2	X3	Y	Y*	dY
1	2	3	4	5	6	7	8
1	1,6285	1,1157	3,0982	7,4363	2,8	3,1314	-0,3314
2	0,4653	1,1500	3,2570	7,1707	0,8	1,3425	-0,5425
2	0,4071	1,1729	3,4159	7,0379	0,7	-0,1566	0,8566
2	0,2908	1,2072	3,5748	6,7060	0,5	-2,2234	2,7234
1	1,6867	1,0871	3,0187	7,4363	2,9	3,2043	-0,3043
1	1,2795	1,1385	3,0982	7,3699	2,2	3,3854	-1,1854
1	2,0356	1,0356	2,8598	7,4363	3,5	3,4829	0,0171
2	0,5235	1,1671	3,2570	7,3035	0,9	2,2971	-1,3971
1	1,9193	1,0070	2,7804	7,5027	3,3	3,8336	-0,5336
1	1,7448	1,0241	2,8598	7,4363	3	3,2170	-0,2170
2	0,2908	1,1900	3,3365	6,6396	0,5	-0,6873	1,1873
1	1,9193	0,9097	2,5421	7,5691	3,3	4,0640	-0,7640
1	1,3959	0,9383	2,7010	7,5027	2,4	2,9757	-0,5757
1	2,2101	1,0584	2,9393	7,4363	3,8	3,2771	0,5229
2	0,5235	1,1557	3,1776	7,2371	0,9	2,4909	-1,5909
1	1,6867	1,1157	3,0982	7,3699	2,9	2,8536	0,0464
2	0,4653	1,1671	3,4159	7,1043	0,8	-0,0117	0,8117
1	2,1520	1,0871	3,0187	7,4363	3,7	3,2043	0,4957

Продолжение таблицы 3
1	2	3	4	5	6	7	8
1	2,3264	1,0928	3,0187	7,4363	4	3,3372	0,6628
2	0,3490	1,1786	3,5748	6,9715	0,6	-1,7767	2,3767
1	2,4428	1,0642	2,9393	7,4363	4,2	3,4100	0,7900
1	2,2101	1,0470	2,9393	7,4363	3,8	3,0112	0,7888
2	0,5235	1,1671	3,2570	7,3035	0,9	2,2971	-1,3971
2	0,4071	1,1786	3,4159	7,1043	0,7	0,2542	0,4458
1	2,0356	1,0298	2,8598	7,5027	3,5	3,6278	-0,1278
2	0,2908	1,2072	3,5748	6,7724	0,5	-1,9455	2,4455
1	1,8612	1,0928	3,0187	7,4363	3,2	3,3372	-0,1372
1	2,2101	1,0012	2,7804	7,5027	3,8	3,7006	0,0994
2	0,4653	1,1557	3,3365	7,1707	0,8	0,7379	0,0621
1	2,2683	1,0184	2,7804	7,5027	3,9	4,0995	-0,1995
2	0,4071	1,1671	3,4159	7,0379	0,7	-0,2896	0,9896
1	1,8612	1,0871	2,8598	7,5027	3,2	4,9573	-1,7573
1	1,4540	1,1099	2,9393	7,4363	2,5	4,4737	-1,9737
2	0,4653	1,1671	3,3365	7,1043	0,8	0,7259	0,0741
1	1,8612	1,0699	2,8598	7,5027	3,2	4,5584	-1,3584
1	1,5122	1,0241	2,7804	7,5027	2,6	4,2324	-1,6324
2	0,2908	1,2072	3,5748	6,6396	0,5	-2,5013	3,0013
1	1,7448	0,9669	2,7804	7,5027	3	2,9029	0,0971
1	1,8612	1,0584	2,8598	7,5027	3,2	4,2925	-1,0925
1	2,0938	1,0985	2,9393	7,4363	3,6	4,2078	-0,6078
2	0,4653	1,1843	3,4159	7,1043	0,8	0,3872	0,4128
1	1,8030	1,0527	2,8598	7,5027	3,1	4,1596	-1,0596
2	0,4653	1,1500	3,2570	7,1707	0,8	1,3425	-0,5425
1	2,0356	1,1042	2,9393	7,5027	3,5	4,6186	-1,1186
1	1,6285	0,9612	2,7804	7,5027	2,8	2,7699	0,0301
1	2,0356	1,0699	2,8598	7,4363	3,5	4,2806	-0,7806
2	0,5235	1,1443	3,1776	7,2371	0,9	2,2250	-1,3250
1	1,6867	1,0985	2,9393	7,4363	2,9	4,2078	-1,3078
2	0,2908	1,2129	3,6542	6,7060	0,5	-2,8280	3,3280
2	0,4071	1,1729	3,4954	7,0379	0,7	-0,8942	1,5942
MO:	1,30E+00	1,10E+00	3,09E+00	7,29E+00	2,232	2,232	-3,18E-15
DIS:	0,5816	0,0057	0,0794	0,0664	1,7194	4,5931	1,5820
SKO:	0,7626	0,0756	0,2819	0,2577	1,3112	2,1431	1,2578

- для первого приема преобразования данных (нормирование и центрирование):

Y(Х)=0,6555+0,0134Х1 – 0,2780Х2+0,0894Х3;

- для второго приема преобразования данных (нормирование по математическому ожиданию):

Y(Х)= –122,3774+0,1127Х – 7576Х2+1,5604Х3;

- для третьего приема преобразования данных (нормирование по дисперсии):

Y(Х)=–-25,1492+0,1329Х1 – ,7376Х2+0,2778Х3

Экзамен. Экзамен, как правило, состоит в оценке ошибки прогнозирования, вероятности правильных решений, рисков потребителя и изготовителя [9]. В ряде случаев оценивают и проверяют на соответствие требованиям ряд других характеристик [10]. Проведем исследование и анализ полученных моделей. Для этого воспользуемся программным комплексом «Прогнозирование 1.3». На рис. 1 приведена зависимость вероятностных характеристик от порога регрессионной функции П для первого приема преобразования данных.

Выводы:

1. Построены прогнозные модели качества паяных соединений (ПС).
2. Проведено прогнозирование регрессионным методом качества паяных соединений используя все признаки паяльных паст. Было произведено нормирование и центрирование данных выборки, их нормировка по математическому ожиданию и дисперсии признаков. Наименьшую дисперсию ошибки имеет первый метод. Наиболее информативным оказался параметр Х3.

Список литературы Прогнозные математические модели качества печатных узлов космической аппаратуры

Чуев, Ю.В. Прогнозирование количественных характеристик процессов/Ю.В. Чуев, Ю.Б. Михайлов, В.И. Кузьмин. -М.: Сов. радио, 1975. 400 с.
Гаскаров, Д.В. Прогнозирование технического состояния и надежности радиоэлектронной аппаратуры/Д.В. Гаскаров, Т.А. Голинкевич, А.В. Мозгалевский. -М.: Сов. радио, 1974. 224 с.
Пиганов, М.Н. Прогнозирование надежности радиоэлектронных средств/М.Н. Пиганов, С.В. Тюлевин//Научно-технические ведомости СПбГПУ. Информатика. Телекоммуникации. Управление. 2009. №1 (72). С. 174-180.
Тюлевин, С.В. Структурная модель индивидуального прогнозирования параметров космической аппаратуры/С.В. Тюлевин, М.Н. Пиганов//Вестник Самарского государственного аэрокосмического университета. 2008. № 1. С. 92-96.
Пиганов, М.Н. Индивидуальное прогнозирование стабильности элементов микросборок/М.Н. Пиганов, О.В. Карпов//Надежность и качество: Труды международного симпозиума. -Пенза: ПГУ, 2001. С. 334-337.
Тюлевин, С.В. Структурная модель индивидуального прогнозирования параметров космической аппаратуры/С.В. Тюлевин, М.Н. Пиганов//Вестник Самарского государственного аэрокосмического университета. 2008. № 1. С. 92-96.
Пиганов, М.Н. Индивидуальное прогнозирование показателей качества элементов и компонентов микросборок/М.Н. Пиганов. -М.: Новые технологии, 2002. 267 с.
Пиганов, М.Н. Прогнозирование надежности радиоэлектронных средств/М.Н. Пиганов, С.В. Тюлевин//Перспективы развития телекоммуникационных систем и информационные технологии: Труды междун. конф. -СПб.: Изд-во Политехн. ун-та, 2008. С. 423-440.
Пиганов, М.Н. Индивидуальное прогнозирование показателей качества элементов микросборок/М.Н. Пиганов. -Самара: СГАУ, 1999. 160 с.
Пиганов, М.Н. Технологические основы обеспечения качества микросборок/М.Н. Пиганов. -Самара: СГАУ, 1999. 231 с.

Еще

Статья научная