Программа определения и анализа ассоциациированности видов в экологических сообществах

Важной 1 частью анализа качественных экологических данных является выявление видовых ассоциаций, обусловленных прямыми (трофические, топические, фориче-ские и др.) и косвенными (общность биото-пических условий, характер питания, защита от хищников) межвидовыми отношениями (Odum, Barrett, 1971). С этой целью было разработано несколько специализированных матричных индексов, для определения уровня значимости которых предлагается использовать одну из девяти рандо-мизационных процедур построения теоретического распределения индекса (Gotelli, 2000). Однако в экологических исследованиях задача определения видовых ассоциаций решается сравнительно редко из-за неочевидности математического аппарата и сложности его реализации.

Автором была разработана статистическая методика выделения положительных и отрицательных ассоциаций видов, позволяющая избежать использования матричных индексов и рандомизационной процедуры определения их уровня значимости. Для этого на бинарной матрице встречаемости видов в экологических пробах ис- пользуются дискретные гипергеометрическое или биномиальное распределения, дающие оценку вероятности наблюдаемой совместной встречаемости пар видов. Критическая область функции распределения (confidence intervals of distribution) позволяет принять одно из трех решений: пара видов отрицательно либо положительно ассоциирована или их совместная встречаемость в пробах носит случайный характер. В качестве альтернативы критической области возможно использование байесовского вывода (Bayesian inference), где в качестве оцениваемого параметра может быть взята любая равномерно распределенная наблюдаемая характеристика, например, общее число проб, а в качестве генеративной функции – функция вероятности дискретного распределения.

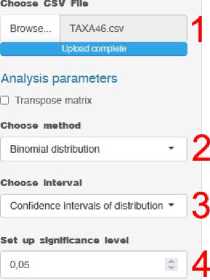
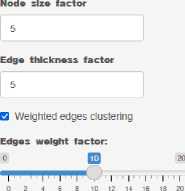
Предложенная методика реализована в виде web-приложения, размещенного на сервере Института биологии внутренних вод по адресу (рис. 1). Приложение написано на языке R в среде Shiny (Chang et al., 2023) и позволяет проанализировать бинарную пользовательскую матрицу формата «виды – пробы» с использованием двух дискретных распределений с заданной критической областью или с помощью байесовских доверительных интервалов (credible intervals of Bayesian inference). Исходная матрица может быть транспонирована для определения ассоциаций между пробами по видовому со- ставу или, другими словами, определения фаунистического сходства. Полученные результаты в виде списка ассоциированных видов или проб могут быть сохранены в формате CSV для дальнейшего анализа.

Species association analysis

® All 301 pairs

О 248 positively associated pairs

О 53 negatively associated pairs

Calculate

Method

i Download

Result

Graph Graph analysis

Search:

Graph parameters

S Species names abbreviations

Nodes position method

Kamada-Kawai (fixed)

Nodes clustering method

Multi-level optimization of modularity

Draw and analyze graph

entries

ChChi.sr chcn.sf 10 11 10 1.00000 0e+00     1 ChChLsr CoBer.sp 10 16 9 1.00000 0e+00     1 ChCri.sf CoBer.sp 11 16 10 1.00000 0e+00     1 ChEuk.gr EpBst.r. 21 36 19 1.00000 0e+00     1 ChRhe.f. EpBst.r. 28 36 23 1.00000 0e+00     1 ChRhe.f. TrHyd.p 28 30 21 1.00000 0e+O0     1 TrHyd.p EpBst.r. 30 36 26 1.00000 0e+00     1 chcrtsf EbEdr.sp 11 20 10 1.00000 ie-05      1 ChRhe.f. SiSim.sp 28 28 19 1.00000 1e-05      1 SiSimsp EpBst.r. 28 36 21 0.99999 2e-05      1 BiEug.a. BiHen. h. 14 14 9 1.00000 2e-05      1 ChChi.sr EbEdr.sp 10 20 9 1.00000 2e-05      1 CoEIm.an EpEpl.i. 13 15 9 1.00000 2e-05      1 StOdn.sp EbEdr.sp 10 20 9 1.00000 2e-05      1 Ollso.m. Ollso.n. 14 14 9 1.00000 2e-05      1 OIRrth OlLim.sp 25 27 17 1.00000 2e-05      1 EpCsn.b CeSph.sp 22 26 15 0.99999 3e-05      1 ChEuk.gr TrHyd.p 21 30 16 0.99999 3e-05      1 OlOph.s. OlSty.la 32 32 21 0.99999 3e-05      1 PoHyp.in DrDre.p. 10 16 8 1.00000 3e-05      1 pit

Рис. 1. Интерфейс web-приложения Species association analysis. Цифрами обозначены: 1 – загрузка пользовательского файла, 2 – выбор статистического распределения, 3 – выбор метода определения видовых ассоциаций, 4 – пороговый уровень значимости, 5 – выбор алгоритма расположения (layout) узлов графа, 6 – выбор алгоритма кластеризации узлов графа Fig. 1. Interface of the Species association analysis web application. The numbers indicate: 1 – loading a user file, 2 – choosing a statistical distribution, 3 – choosing a method for determining species associations, 4 – threshold level of significance, 5 – choosing an algorithm for the layout of graph nodes, 6 – choosing an algorithm for clustering graph nodes

Для визуализации результатов анализа с помощью пакета igraph (Csardi, Nepusz, 2006) приложение строит неориен-тируемый граф, где в качестве узлов представлены виды из списка ассоциированных, а в качестве ребер – выявленные ассоциации между ними. Размер маркера узла пропорционален частоте встречаемости вида, а толщина ребра пропорциональна силе свя- зи через настраиваемые коэффициенты (рис. 2).

Взаимное расположение узлов на графе может быть определено с помощью трех алгоритмов (выпадающий список 5 на рис. 1), одним из которых является метод многомерного шкалирования (MDS). Этот метод часто строит не оптимальный с визуальной точки зрения граф, но расположе- ние вершин в нем несет дополнительную информацию о представленных фаунистических комплексах. На рис. 2 в кластер I входят реофильные пресноводные виды, в кластер II – лимнофильные пресноводные, в кластер III – лимнофильные эвригалин-

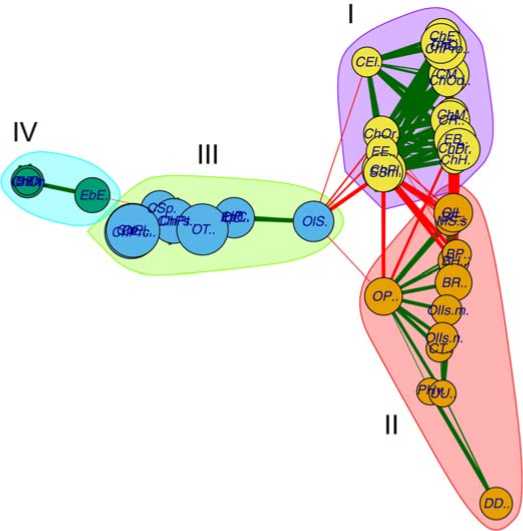
Рис. 2. Граф положительно ассоциированных видов макрозообентоса средних и малых рек бассейна Нижней Волги (Golovatyuk et al., in press). Выделение ассоциаций: биномиальное распределение с 5% верхней критической областью. Расположение вершин методом MDS Fig. 2. Graph of positively associated macrozoobenthos species of medium and small rivers of the Lower Volga basin [Golovatyuk et al. In press]. Identification of associations: binomial distribution with 5% upper critical region. Location of vertices using MDS method

ные, в кластер IV – лимнофильные гало- фильные виды. Таким образом, на графе по оси абсцисс расположен градиент солености воды, а по оси ординат – градиент скорости течения.

Группировка узлов в кластеры также осуществляется с помощью различных алгоритмов, использующих принцип максимизации модулярности графа (выпадающий список 6 на рис. 1). Отдельно можно выделить алгоритм Optimal community structure, добивающийся максимально возможной модулярности средствами целочисленного программирования, но имеющий экспоненциальную сложность (Brandes et al., 2008). Если в визуализацию включены отрицательно ассоциированные виды, задачей алгоритма кластеризации является максимизация отрицательных и минимизация положительных связей между кластерами. Эту задачу успешно решает доработанный алгоритм Affiinity propagation, корректно обрабатывающий отрицательные веса ребер (Traag, Bruggeman, 2008), тогда как остальные алгоритмы считают их нулевыми.

В приведенном рис. 2 кластеризация по- ложительно ассоциированных видов осуществлялась методом многоуровневой оптимизации модулярности (Muli-level optimization of modularity) (Blondel et al., 2008). Кроме указанных выше солености и скорости течения, распределенных по ортогональным осям графа, алгоритм кластеризации учел температуру воды и тип грунта, не имея о них явных данных. Так от кластера I к кластеру IV температура воды в летний период последовательно повышается с 16,9 °C до 27°C, а грунт меняется от гравийно-галечного через заиленный песок и глину до черного ила в кластере IV.

В web-приложении на вкладке «Graph analysis» выделенные кластеры анализируются по плотности связей и их средней силе в кластере. Интегральная характеристика, названная «общей силой связности» (total connectivity strength) объединяет относительное число и среднюю силу связей в кластере в единую нормированную характеристику, позволяющую сравнивать кластеры между собой.

Предложенная методика отличается простотой реализации (для проверки степени ассоциированности видов возможно использование MS Excel 2010+), а также устойчивостью и воспроизводимостью ре

СПИСОК