Программирование на языке Prolog интеллектуальных задач

Вводные замечания

Prolog – язык логического программирования. «Логическое программирование – это подход к программированию, при котором в качестве языка высокого уровня используется логика предикатов первого порядка в форме фраз Хорна. Логическое программирование дает возможность программисту описывать ситуацию при помощи формул логики предикатов, а затем для выполнения выводов из этих формул применить автоматический решатель задач» [2]. При этом основное внимание уделяется описанию логической структуры прикладной задачи.

Разработка языка Prolog началась в 1970 г. сотрудниками Эдинбургского университета Аланом Кулмероэ и Филиппом Расселом [там же]. Их целью было создание языка программирования, который мог бы делать логические выводы на основе заданного текста. Название Prolog является сокращением от Programming in logic. Основной вклад в развитие теории логического программирования внесла работа Р. Ковальского «Логика предикатов как язык программирования» [3]. В 1976 г. Ковальский и М. ван Эмден предложили два подхода к прочтению текстов логических программ – процедурный и декларативный. Оба этих подхода стали активно использоваться при написании программ на язык е Prolog.

Практика программирования с---------------------------------------------------------------------------------------------------------------\

Ланец Сергей Андреевич кандидат физико-математических наук, доцент кафедры вычислительной техники и компьютерной графики Дальневосточного государственного университета путей сообщений. Сфера научных интересов: математическое моделирование, математическая экономика, эконометрика, нейронные сети, системы искусственного интеллекта. Автор около 20 опубликованных научных работ.

В настоящее время существует большое количество различных, но довольно похожих между собой вариантов данного языка: SWI-Prolog, Тurbo Prolog, Quintus Prolog, CProlog, Prolog-2, Arity Prolog, Silogic Knowledge Workbench, Prolog-86, Prolog-D и др. Хотя единого стандарта языка Prolog не существует, версия, разработанная в Эдинбургском университете, стала наиболее широко используемой [2].

Prolog применяется при решении большого класса задач, связанных с разработкой систем искусственного интеллекта (экспертные системы, составление сложных расписаний, интеллектуальные игры, программы-переводчики). Он используется для обработки естественного языка и обладает большими возможностями, позволяющими обрабатывать информацию из баз данных.

В настоящее время Prolog продолжает развиваться и вбирает в себя новые современные технологии и концепции программирования.

В Дальневосточном государственном университете путей сообщений (г. Хабаровск) в рамках преподавания дисциплины «Системы искусственного интеллекта» рассматриваются решения различных интеллектуальных задач с использованием языка Prolog. Такими интересными задачами являются классические задачи о расстановке шахматных фигур на доске – задача о 8 ферзях и задача о 5 ферзях. Решение этих задач на Prolog помогает осваивать логику этого языка и развивает навыки решения интеллектуальных задач.

Задача о 8 ферзях

Задача о 8 ферзях состоит в отыскании такой расстановки восьми ферзей на шахматной доске размером 8х8, при которой ни один из ферзей не находится под боем другого.

Рассмотрим решение этой задачи, опирающееся на решение, приведенное в учебнике И. Братко [1].

Решение мы зададим как отношение:

решение( Поз), где Поз изображает позицию, в которой ферзи не бьют друг друга.

Представим позицию в виде списка из 8 элементов, каждый из которых соответствует одному из ферзей. Каждое поле доски можно описать с помощью пары координат Х и Y,

Программирование на Прологе интеллектуальных задач целых чисел от 1 до 8. В программе мы будем записывать такую пару в виде двоичного списка [X|Y]. Тогда задача сводится к нахождению списка вида

[[X1|Y1], ..., [X8|Y8]]

Поскольку мы знаем, что во избежание нападений все ферзи должны находиться на разных вертикалях, мы можем ограничить перебор в виде шаблона:

[[1|Y1], [2|Y2], [3|Y3], [4|Y4], [5|Y5], [6|Y6], [7|Y7], [8|Y8]]

Тогда отношение решение можно сформулировать, рассмотрев два случая [1]:

«1. Список ферзей пуст. Пустой список является решением, так как нападений в этом случае нет.

• 2.    Список ферзей не пуст. Представим его так:

[[X|Y] | Остальные ]

В этом случае первый ферзь на поле [X|Y], а остальные – на полях в списке Остальные . Необходимо соблюдение следующих условий:

• (1)    Ферзи в списке Остальные не бьют друг друга, то есть список Остальные сам должен быть решением.

• (2)    Х и Y должны быть целыми числами от 1 до 8.

• (3)    Ферзь на поле [X|Y] не должен бить ферзей из списка Остальные » [1].

Чтобы задать первое условие, воспользуемся самим отношением решение . Второе условие: Y принадлежит списку [1, 2, 3, 4, 5, 6, 7, 8] , о координате Х можно не беспокоиться, поскольку список-решение должен соответствовать шаблону, у которого Х-ко-ординаты уже заданы и различны. Третье условие можно обеспечить с помощью нового отношения небьет . Все это можно записать на Prolog так:

решение([X|Y] | Остальные] ) :- решение( Остальные), принадлежит (Y, [1, 2, 3, 4, 5, 6, 7, 8]), небьет([X|Y], Остальные).

Определим отношение небьет : « небьет( Ф, Фспис) как два случая [1]:

• (1)    Если список Фспис пуст, то отношение выполнено (некого бить).

• (2)    Если Фспис не пуст, то он имеет вид [Ф1 | Фспис1]

и должны также выполняться два условия:

• (а)    ферзь на поле Ф не бьет ферзя на поле Ф1 и

• (b)    ферзь на поле Ф не бьет ферзей из списка Фспис1 .

Условие, чтобы ферзь на некотором поле не бил другое поле, довольно простое: эти поля должны находиться на разных вертикалях, горизонталях и диагоналях. Наш шаблон решения гарантирует, что все ферзи находятся на разных вертикалях, поэтому остается обеспечить, чтобы

• •    Y-координаты были различны и

• •    ферзи находились на разных диагоналях, то есть расстояние между полями по оси Х не должно равняться расстоянию между ними по оси Y».

На рисунке 1 приведена программа для решения задачи.

?- шаблон (S), решение( S).

Практика программирования решение ([]).

решение ([[X|Y] | Остальные’]) :-решение(Остальные’), принадлежит (Y, [1, 2, 3, 4, 5, 6, 7, 8]), небьет ([X|Y], Остальные’).

небьет (, [ ]).

небьет ([X|Y] ,[[X1|Y1] | Остальные] ) :-

Y =\= Y1,

• Y1-Y =\= X1-X ,

• Y1-Y =\= X-X1,

Небьет ([X|Y], Остальные).

принадлежит (X, [X | L]).

принадлежит (X, [Y | L] ) :- принадлежит (X, L).

шаблон ([[1|Y1], [2|Y2], [3|Y3], [4|Y4], [5|Y5], [6|Y6], [7|Y7], [8|Y8]])

Рис. 1. Программа для задачи о восьми ферзях

После запуска программы она будет генерировать решения в таком виде:

S=[[1|4],[2|2],[3|7],[4|3],[5|6],[6|8],[7|5],[8|1]]

S=[[1|5],[2|2],[3|4],[4|7],[5|3],[6|8],[7|6],[8|1]]

S=[[1|3],[2|5],[3|2],[4|8],[5|6],[6|4],[7|7],[8|1]]

Всего 92 решения задачи.

Таким образом, мы продекларировали только общие условия решения, и программа сама отыскала решение.

Задача о 5 ферзях

Задача состоит в отыскании такой расстановки пяти ферзей на пустой шахматной доске 8х8, при которой ни один из ферзей не находится под боем другого, но все клетки шахматной доски были бы биты ими. 5 ферзей – это минимальное количество ферзей, при которых бьется все поле. Решение этой задачи опирается на технику рассмотренной выше задачи о 8 ферзях.

Рассмотрим сначала частные решения. Одним из частных решений задачи является размещение ферзей в первых пяти горизонталях и вертикалях так, чтобы они не били друг друга (рис. 2), но стояли бы на диагоналях, пробивающих правый верхний прямоугольник 6<=X<=8 ; 6<=Y <=8 (серые клетки).

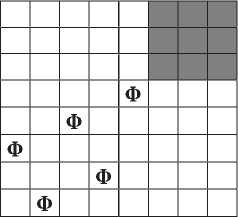
Рис. 2. Решение задачи о 5 ферзях в первом нижнем пятиугольнике

Программирование на Прологе интеллектуальных задач

Это достигается изменением области принадлежности Y:

принадлежит (Y, [1, 2, 3, 4, 5]).

И изменением шаблона:

шаблон([[1|Y1], [2|Y2], [3|Y3], [4|Y4], [5|Y5]]).

Они также не должны бить друг друга, но должны пробивать через диагонали правый верхний сектор, то есть ячейки 6<=X<=8 ; 6<=Y <=8.

Диагонали, идущие вверх, задаются соотношением U = X – Y, диагонали, идущие вниз, задаются как V = X + Y (рис. 3).

u = x - y z7

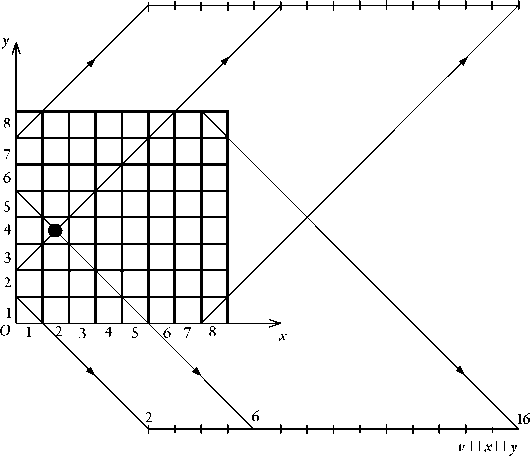
Рис. 3. Связь между вертикалями, горизонталями и диагоналями

Помеченное поле имеет следующие координаты:

x = 2, у = 4, u = 2 – 4 = –2, v = 2 + 4 = 6.

Тогда диагонали, идущие вверх, U = X – Y, пробивающие верхний сектор, то есть ячейки: 6<=X<=8 ; 6<=Y <=8, принадлежат списку [–2,–1,0,1,2].

На Prolog это задается так:

U is X – Y, принадлежит (U, [-2,-1,0,1,2]).

И тогда с учетом этого модифицируется отношение решение . Все остальное остается неизменным (рис. 4):

Практика программирования решение ([ ]).

решение ([[X|Y] | Остальные]):- решение( Остальные), принадлежит (Y, [1, 2, 3, 4, 5]),

U is X – Y, принадлежит (U, [-2,-1,0,1,2]), небьет ([X|Y] | Остальные). небьет (, [ ]).

небьет ([X|Y] , [[X1|Y1] | Остальные]) :- Y =\= Y1,

Y1-Y =\= X1-X , Y1-Y =\= X-X1, небьет([X|Y] , Остальные). принадлежит (X, [X | L]). принадлежит (X, [Y | L]) :- принадлежит( X, L). шаблон ([[1|Y1], [2|Y2], [3|Y3], [4|Y4], [5|Y5]]). ?- шаблон( S), решение( S).

Рис. 4. Программа для задачи о 5 ферзях

Данная программа находит 4 допустимых решения для ферзей в первых пяти вертикалях и горизонталях:

S=[[1|1],[2|4],[3|2],[4|5],[5|3]]

S=[[1|1],[2|3],[3|5],[4|2],[5|4]]

S=[[1|3],[2|1],[3|4],[4|2],[5|5]]

S=[[1|2],[2|4],[3|1],[4|3],[5|5]]

Изменяя области допустимости X и Y, а также области допустимости диагоналей, несложно получить другие частные решения. При этом мы получаем частные решения задачи с компактным положением ферзей в соседних вертикалях и диагоналях.

Например, мы можем задать область изменения X c 4 по 8 значение через шаблон: шаблон ([4|Y1], [5|Y2], [[6|Y3], [7|Y4], [8|Y5]]).

Y координату оставить прежней: принадлежит (Y, [1, 2, 3, 4, 5]), а диагонали в этом случае задать как: U is X + Y, принадлежит (U, [7,8,9,10,11]) Тогда мы получим компактное решение при X c 4 по 8 и Y c 1 по 5.

Общее решение

Если мы хотим найти общее решение задачи, не привязанное к какой-либо конкретной области доски, то нам надо ввести отношение, которое бы проверяло, все ли поля шахматной доски находятся под боем наших ферзей.

Для этого введем отношение доска ( ) как список всех полей шахматной доски: доска ([[1|1],[1|2],[1|3],[1|4],[1|5],[1|6],[1|7],[1|8], [2|1],[2|2],[2|3],[2|4],[2|5],[2|6],[2|7],[2|8], [3|1],[3|2],[3|3],[3|4],[3|5],[3|6],[3|7],[3|8], [4|1],[4|2],[4|3],[4|4],[4|5],[4|6],[4|7],[4|8], [5|1],[5|2],[5|3],[5|4],[5|5],[5|6],[5|7],[5|8], [6|1],[6|2],[6|3],[6|4],[6|5],[6|6],[6|7],[6|8], [7|1],[7|2],[7|3],[7|4],[7|5],[7|6],[7|7],[7|8], [8|1],[8|2],[8|3],[8|4],[8|5],[8|6],[8|7],[8|8]]).

Программирование на Прологе интеллектуальных задач

Далее будем удалять из нашей доски все клетки, которые находятся под боем ферзя на позиции [X|Y] . Для этого нам надо исключить все горизонтали, вертикали и диагонали для этого ферзя. И так для всех ферзей из списка Решение . Если в результате исключения список небитых клеток останется пустым, то это и будет решением задачи.

Для этого вводим отношение разность (L1, L2, L) двух списков L1 и L2, которое находит список L, равный вычету из L1 элементов, входящих в L2, то есть удаляются элементы, принадлежащие одновременно L1 и L2:

разность ([], _, []).

разность ([X | L1], L2, L):- принадлежит (X, L2), !, разность (L1, L2, L).

разность ([X | L1], L2, [X | L]):- разность (L1, L2, L).

Вводим рекуррентную функцию диаг_удалить (X,Y,n,D,L), удаляющую из множества D поля, стоящие на диагоналях, битые ферзем на позиции [X|Y]. При этом множество L будет результатом этого исключения.

диаг_удалить(X,Y,1,D,L) :- Y2 is 1-X+Y,

Y3 is X+Y-1, разность(D,[[1|Y2],[1|Y3]],L).

диаг_удалить(X,Y,n,D,L) :- n >0, 9> n,

Y2 is n-X+Y, Y3 is X+Y-n, разность(D,[[n|Y2],[n|Y3]],L2), m is n-1, диаг_удалить(X,Y,m,L2,L).

Вводим общую рекуррентную функцию Свободные(Doska,Решение,Не_Би-тые) , которая последовательно перебирает ферзей на позиции [X|Y] из множества Решение и вычитает из доски Doska диагонали (диаг_удалить(X,Y,8, Doska ,L0)), вертикали [[X|1], ..., [[X|8]] и горизонтали [[1|Y], …, [[8|Y]]. Результатом является множество позиций Не_Битые, которые не бьются ферзями из списка Решение. Нас интересует ситуация, при которой это множество будет пустым.

Свободные([],Решение,[]).

Свободные(Doska,Решение,Не_Битые) :-

Решение <>[],

[[X|Y] | Остальные]) = Решение, диаг_удалить(X,Y,8,Doska,L0), разность(L0,[[X|1],[[X|2],[[X|3],[[X|4],[[X|5],[[X|6],[[X|7],[[X|8]], L1), разность(L1,[[1|Y],[[2|Y],[[3|Y],[[4|Y],[[5|Y],[[6|Y],[[7|Y],[[8|Y]], L), Свободные(L,Остальные, Не_Битые).

Практика программирования

Шаблон решения задаем в общем виде из 5 позиций ферзей:

шаблон ([[X1’|Y1’], [X2’|Y2’], [X3’|Y3’], [X4’|Y4’], [X5’|Y5’]]).

Собираем введенные функции в одну общую функцию с целью избежать печати при каждом решении всех полей доски:

решение_общее( S):- доска( Doska),

НЕ_битые(Doska,S,Битые),

Битые = [].

И далее вызываем решение задачи:

? шаблон (S), решение( S), решение_общее( S).

Еще некоторое дополнение делается в функцию небьет([X|Y], [[X1|Y1] | Остальные]). Добавляется условие, что

X1 > X , для упорядочения Х координаты и исключения перестановок одного и того же решения. В противном случае программа будет выдавать одинаковые решения, переставляя одни и те же позиции в разные места списка Решение и считая их разными решениями.

Реализация программы в версии SWI Prolog будет выглядеть следующим образом:

belong( X, [X | _] ).

belong( X, [_| L] ) :- belong( X, L).

delta( [], _, []).

delta( [X | L1], L2, L):- belong( X, L2), !, delta( L1, L2, L).

delta( [X | L1], L2, [X | L]) :- delta( L1, L2, L).

desk([[1|1],[1|2],[1|3],[1|4],[1|5],[1|6],[1|7],[1|8],

[2|1],[2|2],[2|3],[2|4],[2|5],[2|6],[2|7],[2|8],

[3|1],[3|2],[3|3],[3|4],[3|5],[3|6],[3|7],[3|8],

[4|1],[4|2],[4|3],[4|4],[4|5],[4|6],[4|7],[4|8],

[5|1],[5|2],[5|3],[5|4],[5|5],[5|6],[5|7],[5|8],

[6|1],[6|2],[6|3],[6|4],[6|5],[6|6],[6|7],[6|8],

[7|1],[7|2],[7|3],[7|4],[7|5],[7|6],[7|7],[7|8], [8|1],[8|2],[8|3],[8|4],[8|5],[8|6],[8|7],[8|8]]).

solution([]).

solution( [[X|Y] |Rest] ) :- solution(Rest), belong(Y,[1, 2, 3, 4, 5 ,6 ,7, 8]), belong(X,[1, 2, 3, 4, 5 ,6 ,7, 8]), not_beat( [X|Y],Rest).

not_beat( _,[]).

not_beat( [X|Y] ,[[X1|Y1] |Rest] ) :- Y =\= Y1,

X1 > X,

K is Y1 -Y,

L is X1 -X, M is X -X1,

K=\= L, K=\= M ,

Программирование на Прологе интеллектуальных задач not_beat([X|Y],Rest).

diag_delete(X,Y,1,D,L) :- Y2 is 1-X+Y,

Y3 is X+Y-1 , delta(D,[[1|Y2],[1|Y3]],L). diag_delete(X,Y,N,D,L) :- N >0, 9 > N , Y2 is N-X+Y ,

Y3 is X+Y-N, N2 is N - 1, delta(D,[[N|Y2],[N|Y3]],L2), diag_delete(X,Y,N2,L2,L).

free([],_,[]) .

free(D,[],D) .

free(Doska,Solve,Free_cells) :- [[X|Y] | Rest]= Solve , diag_delete(X,Y,8,Doska,L0), delta(L0,[[X|1],[X|2],[X|3],[X|4],[X|5],[X|6],[X|7],[X|8]], L1), delta(L1,[[1|Y],[2|Y],[3|Y],[4|Y],[5|Y],[6|Y],[7|Y],[8|Y]], L), free(L, Rest,Free_cells).

shablon( [[X1|Y1], [X2|Y2], [X3|Y3], [X4|Y4], [X5|Y5]]).

general_solution( S):-shablon(S),solution(S), desk(Doska), free(Doska,S,Free_cells), Free_cells = [].

?-general_solution( S).

Программа генерирует решения:

• 1.    S=[[1|6],[2|2],[5|7],[6|3],[7|1]]

• 2.    S=[[1|5],[2|2],[4|7],[6|4],[7|1]]

• 3.    S=[[1|4],[2|2],[4|6],[6|5],[7|1]]

• 4.    S=[[1|6],[2|2],[5|7],[6|5],[7|1]]

• 5.    S=[[2|2],[3|6],[5|7],[6|5],[7|1]]

Всего она выдает 728 решений задачи. И уже из первых решений видно, что они лежат не обязательно в соседних вертикалях и горизонталях.

Таким образом, мы построили общее решение задачи, задавая только общие правила поиска решения сформулированной задачи. Действуя по этим правилам, Prolog сам ищет ее решение. В этом суть его логической и декларативной природы.