Программная реализация движения Parrot Ar.Drone 2.0. по пользовательской траектории

• •    Через порт 5554 квадрокоптера по протоколу UDP происходит инициализация канала связи для передачи по нему навигационных данных(статус работы, высота и скорость полета, направление и другое).

• •    С портов 5559 и 5555 дрона по протоколу TCP происходит передача конфигураций и видеопотока с одной из камер соответственно.

• •    Управление осуществляется через UDP-порт 5556. На него передаются так называемые AT-команды, в которых и заложены непосредственные инструкции для квадрокоптера.

Каждая AT-команда представляет собой строку, оканчивающуюся символом конца строки и имеющую следующую конструкцию:

AT*[имя команды]=[порядковый номер][параметр 1, параметр 2…]

Ниже приведены названия команд, используемых в данной работе и их назначение.

• •    REF - базовые действия: взлет, посадка, аварийное выключение и перезапуск. Параметры: число, соответствующее конкретному действию.

• •    PCMD - передвижение дрона во время полета. Параметры: служебный флаг, крен, тангаж, рыскание, газ.

• •    FTRIM - сообщает дрону о том, что тот находится в горизонтальном положении, для его ориентации в пространстве во время дальнейшего полета. Параметры: нет.

Требуется следить за порядковыми номерами при передаче команд. Дрон обработает инструкцию только в том случае, если номер новой команды больше номера предыдущей.

Была разработана программа на С/С++, позволяющая отправить дрон в полет по нарисованной пользователем траектории. Цикл работы программы продемонстрирован на UML-диаграммe(рис.2).

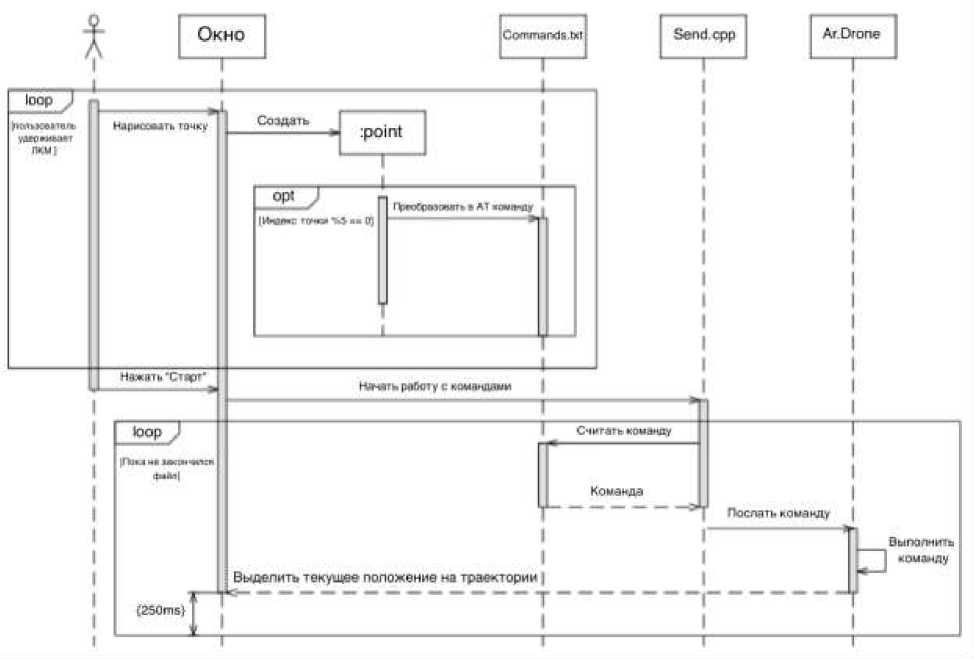
Рис. 2. UML-диаграмма работы программы.

Для передачи AT-команд используются сокеты. Сокет открывается при инициализации объекта класса квадрокоптера. Для каждой команды предусмотрен отдельный метод, использующий ранее открытый сокет для передачи пакета.

Значения большинства параметров задаются с помощью IEEE-754 – стандарта, описывающего формат представления чисел с плавающей точкой.

В программе предусмотрены следующие действия с квадракоптером: Взлет:

Формат AT-команды: AT*REF= [порядковый номер],290718208.

290718208 – число, соответствующее взлету в команде REF.

Дрон поднимается на 1 метр над поверхностью. Для предотвращения конфликтов с последующими командами задается задержка программы на 7 секунд.

Листинг открытия сокета и метода взлета приведены ниже, а их алгоритм описан на рис. 3. Остальные методы реализованы схожим образом: class Drone{ public:

int i;

struct sockaddr_in receiver_addr;

int sock_fd;

char droneBuf[50];

Drone() { i = 1;

sock_fd = socket(AF_INET, SOCK_DGRAM, IPPROTO_UDP); receiver_addr.sin_family = AF_INET;

if (inet_aton( "192.168.1.1", &receiver_addr.sin_addr ) == 0) { close(sock_fd);

return;

} receiver_addr.sin_port = htons( PORT );

} void droneTakeOff() { sprintf(droneBuf,"AT*REF=%u,290718208\r",i++);

sendto(sock_fd, droneBuf, 50, 0,(struct sockaddr*)&receiver_addr, sizeof(receiver_addr));

std::cout << "away from land" << std::endl;

sleep(7);

}

// …

}

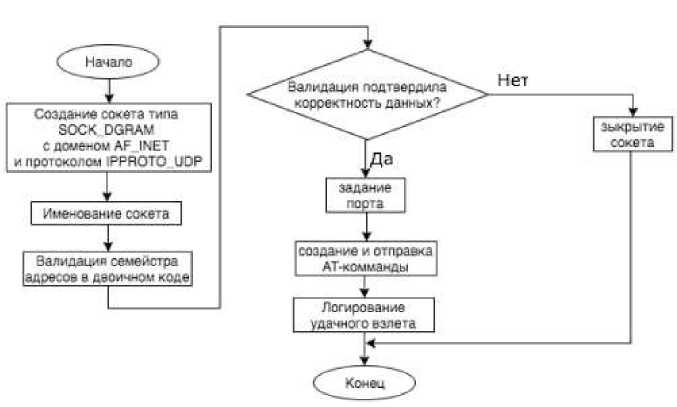
Рис. 3. Алгоритм открытия сокета и взлета.

Калибровка:

Формат АТ-комманды: AT*FTRIM=[порядковый номер].

Вызывается перед взлетом для правильной ориентации дрона в пространстве.

Посадка:

Формат АТ-команды: AT*REF= [порядковый номер],290717696.

290717696 – число, соответствующее посадке в команде REF.

Движение вперед:

Формат AT-команды:   AT*PCMD=[порядковый номер],1,0,-

1082130432,0,0.

Число -1082130432 соответствует исходному числу -1, что означает, что выставлен минимальный тангаж и дрон полетит вперед в горизонтальной плоскости. Служебный флаг установлен в 1, как и для всех действий, связанных с движением. Значения крена, рысканья и газа установлены в 0. Перед обращением к дрону вычисляется количество необходимых вызовов АТ-команды.

Повороты влево и вправо:

Форматы АТ-команд:

Поворот влево: AT*PCMD=[порядковый номер],1,0,0,0,-1090519040

Поворот вправо: AT*PCMD=[порядковый номер],1,0,0,0, 1056964608

Числа -1090519040 и 1056964608 соответствуют -0,5 и 0,5, т.е. команды поворота влево и вправо отличаются только значениями рыскания. Данные числа определяют угол поворота в 15 градусов. Значение тангажа, крена и газа установлены в 0.

На вход модулю, отвечающему за обработку координат, принятых от клиентского приложения, подаются координаты в таком виде: сначала количество координат, которые нужно обработать, затем сами координаты (первая по X, вторая по Y). После записи всех координат в массив struct point { data_t x;

data_t y;

};

typedef point point_t;

point_t* arr_crd = new point_t[qty_crd];

for (int pos = 0; pos < qty_crd; pos++) { std::cin >> arr_crd[pos].x >> arr_crd[pos].y;

} происходит взлет квадрокоптера с помощью функции droneTakeOff() из класса Drone.

Обработка координат. Как только дрон взлетел, все его дальнейшие перемещения будут описаны в двух координатных осях – ОХ и OY. Для работы с осями следует назначить дрону, после того как он взлетит, начальное значение координат и начальный основной вектор движения. Основной вектор движения – это направленный отрезок, находящийся под углом α относительно положительной полуоси абцисс единичной окружности. Для обозначения на плоскости вектора в данной работе достаточно знать только угл α , им и будем обозначать основной вектор движения. Однако вектор будет обозначен не всеми значениями угла α, а только кратными 15-ти. Данная погрешность допустима в рамках целей использования квадрокоптера.

Следовательно, обозначение вектора лежит в диапазоне [0, 15, 30, … , 330, 345, 360], где крайние, включенные в диапазон значения обозначают один и тот же вектор.

Начальные значения могут быть выбраны любыми, так как вся дальнейшая работа будет связана исключительно с их разностями (дельтами). Для удобства были выбраны координаты (0, 0) и основной вектор движения – ось координат OY.

Для корректной обработки каждой координаты нужно посчитать два измерения:

• 1.    Как изменится основной вектор движения дрона относительно прошлой координаты.

• 2.    Насколько дрон нужно переместить вперед в пространстве.

Изменение основного вектора движения дрона. Рассмотрим функцию:

void turn(int curent_drone_vector, int need_drone_vector, drone Ardrone) { int delta_angle = need_drone_vector - curent_drone_ vector;

Ardrone.droneRotateRight(pos);

}

Где curent_drone_vector – обозначение текущего вектора основного движения дрона, need_drone_vector – нужный вектор, delta_angle – угл, на который нужно повернуть дрон, чтобы изменить его основной вектор движения с текущего на нужный, droneRotateRight(х) – функция из класса Drone,   которая поворачивает дрон на х градусов направо, droneRotateLeft(х) – налево.

В функции turn() обрабатывается 5 событий:

• 1.    Если delta_angle > 0 и delta_angle <= 180, то поворачиваем направо на delta_angle градусов.

• 2.    Если delta_angle > 180, то поворачиваем налево на 360 -

• abs(delta_angle), где abs(х) – функция взятия модуля от х.

• 3.    Если delta_angle < 0 и delta_angle >= -180, то поворачиваем налево на abs( delta_angle).

• 4.    Если delta_angle < -180, то поворачиваем направо на 360 -abs( delta_angle ).

• 5.    Если curent_drone_vector = need_drone_vector , то не поворачиваем никуда.

Перемещение дрона вперед в пространстве. Существуют “простые” и “сложные” случаи. Под “простыми” подразумевается, что delta_x = 0 или delta_y = 0 , где delta_x – разность между текущей и следующей координатой дрона по оси ОХ, delta_y – по OY.

Рассмотрим 4 “простых” случая:

• 1.    Если delta_x == 0 и delta_y > 0, то вызываем функции

• 2.    Если delta_x == 0 и delta_y < 0, то turn(curent_drone_angle, 180 , Ardrone) и Ardrone.droneForward(abs( delta_y )).

• 3.    Если delta_x > 0 и delta_y == 0, то turn(curent_drone_angle, 90 , Ardrone) и Ardrone.droneForward( delta_x ).

• 4.    Если delta_x < 0 и delta_y == 0, то turn(curent_drone_angle, 270 , Ardrone) и Ardrone.droneForward(abs( delta_x) ).

turn(curent_drone_angle,          0 ,         Ardrone)         и

Ardrone.droneForward( delta_y ), где droneForward(х) - функция из класса Drone , которая двигает дрон на x единиц вперед.

Для рассмотрения “сложных” случаев понадобится функция, которая находит текущее положение вектора - find_drone_vector(int opposite_leg, int adjacent_leg). opposite_leg – противолежащий катет треугольника, образованного соединением текущей координаты со следующей и достраиванием delta_x и delta_y. adjacent_leg – прилежащий катет этого же треугольника. В зависимости от ситуации прилижащим катетом будет либо delta_x, либо delta_y, это же касается и противолежащего катета. Рассмотрим код функции:

int Find_drone_vector(int opposite_leg, int adjacent_leg) { double angle = asin(abs(opposite_leg) / sqrt(adjacent_leg * adjacent_leg + opposite_leg * opposite_leg));     // теорема пифагора angle = 180 * angle / pi;                     // перевод из радиан int integer_angle = angle / 15;                 // целая часть return (integer_angle + 1) * 15;

}

Рассмотрим 4 “сложных” случая:

• 1.    Если delta_x > 0 и delta_y > 0, то

• 2.    Если delta_x > 0 и delta_y < 0, то

• 3.    Если delta_x < 0 и delta_y < 0, то turn(curent_drone_angle, Find_drone_vector( delta_x , delta_y) + 180 , Ardrone); int f = sqrt(delta_y * delta_y + delta_x * delta_x);

• 4.    Если delta_x < 0 и delta_y > 0, то turn(curent_drone_angle, Find_drone_vector( delta_y , delta_x) + 270 , Ardrone); int f = sqrt(delta_y * delta_y + delta_x * delta_x);

turn(curent_drone_angle, Find_drone_vector( delta_x , delta_y), Ardrone);

int f = sqrt(delta_y * delta_y + delta_x * delta_x);      //Теорема пифагора

Ardrone.droneForward(f);

turn(curent_drone_angle, Find_drone_vector( delta_y , delta_x) + 90 , Ardrone); int f = sqrt(delta_y * delta_y + delta_x * delta_x);

Ardrone.droneForward(f);

Ardrone.droneForward(f);

Ardrone.droneForward(f);

Рассмотрим пример. Допустим, начальные координаты дрона указаны как (1, 3) (Рис. 4). Начальное обозначение основного вектора движения – 0.

Перваю смену координат (1,3) -> (2,3) описывает “простой” случай №3: Поворачиваем дрон на 90 градусов направо и двигаемся вперед на delta_x = 1.

Вторую смему координат (2,3) -> (3,1) описывает “сложный” случай №2: Find_drone_vector() вернет 75. Следовательно нужное обозначение вектора = 75 + 90 = 165. Функция turn() вызывается со следующими параметрами – turn(90, 165, Ardrone), что означает поворот направо на 75 градусов.

Далее двигаемся вперед на sqrt((-2) * (-2) + 1 * 1)

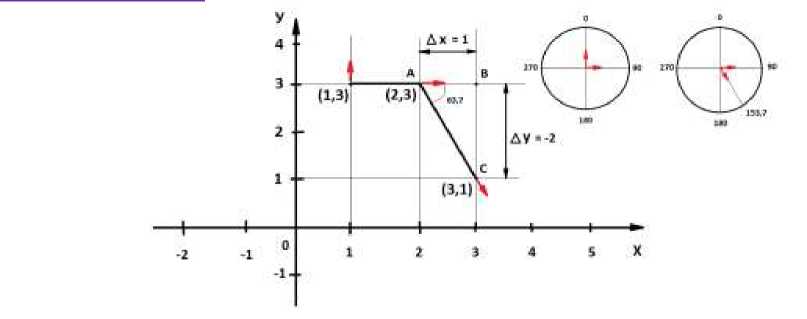
Рис. 4. Траектория движения дрона.

Взаимодействие с пользователем. Для создания интерфейса пользователя(Рис. 5) в качестве среды разработки был выбран Qt Designer. Библиотека Qt в числе прочих содержит множество графических элементов, удобных с точки зрения как разработки, так и эксплуатации программы.

Особенностью Qt является использование системы сигналов и слотов, что находит наибольшее применение именно в графических интерфейсах. Данный подход подразумевает, что компоненты приложения посылают некоторую информацию о событиях(сигналы) и могут принимать и обрабатывать сигналы от других компонентов с помощью своих методов, помеченных как слоты.

С точка зрения пользователя, взаимодействие с дроном выглядит следующим образом:

• 1.    Пользователь нажимает ЛКМ и, не отпуская ее, рисует произвольную линию.

• 2.    Пользователь отпускает ЛКМ.

• 3.    Пользователь нажимает кнопку “Start”.

• 4.    Дрон поднимается в воздух и начинает движение по линии от первой нарисованной точки.

• 5.    Каждый раз, когда дрон пролетает небольшой участок линии, соответствующая точка помечается красным, а ее координаты выводятся в текстовое поле рядом с полем для рисования.

• 6.    Пролетев всю  траекторию, дрон опускается  на землю.

Пользователь может очистить поле для рисования с помощью кнопки “Clear” или отправить дрон по уже пройденной траектории.

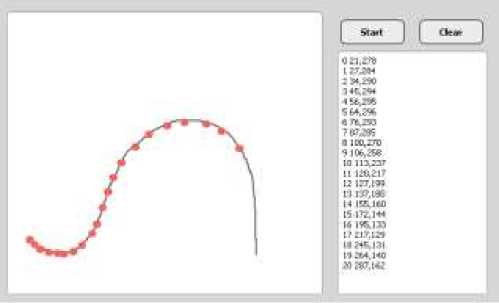
Рис.5. Интерфейс пользователя.

Основной объект в интерфейсе – поле для рисования – создан на основе класса QGraphicsScene. Контейнером для данного поля является объект класса QGraphicsView.

Для определения актуальных размеров графической сцены при запуске программы и изменении размеров окна устанавливается таймер(объект QTimer) на 100 миллисекунд. Задержка необходима, так как непосредственно в момент события изменения размеров окна(resizeEvent) ширина и высота еще не принимают новых значений.

Для осуществления процесса рисования переопределены два события QGraphicsScene: mousePressEvent(событие нажатия ЛКМ) и mouseMoveEvent(событие, сообщающее о том, что мышь сдвинута при зажатой ЛКМ).

При нажатии ЛКМ перехватываются координаты точки, в которой пользователь нажал на кнопку, и вокруг них отрисовывается круг диаметром 2 пикселя. Координаты сохраняются в переменную previous_point. При движении мыши считываются координаты следующей точки, и проводится линия толщиной 2 пикселя между новой точкой и точкой с координатами из previous_point. В previousPoint записываются новые координаты. Данные действия повторяются, пока пользователь не закончит рисование.

Когда дрон достигает очередной точки из массива points, вызывается пользовательское событие pointReachEvent. Соответствующий слот pointReached обеспечивает уведомление пользователя о проделанном пути с помощью выделения достигнутой точки красным(рисуется красный круг диаметром 10 пикселей).

Рядом с полем для рисования находится текстовое поле(объект QTextView), в которое при возникновении pointReachEvent записываются координаты достигнутой точки.

Вывод. Представленная программа ориентирована на эксплуатацию в развлекательных целях, однако может быть полезна и в других областях. С помощью данной программы можно организовать предсказуемое взаимодействие между несколькими квадракоптерами, получить контроль над дроном в условиях плохой видимости(если местность заранее хорошо известна) и другое. Применение программы ограничено фантазией конечного пользователя.