Программная реализация математической модели кинетостатического расчета плоских рычажных механизмов

Глобальная компьютеризация предопределила доминирующее положение аналитических методов исследования механизмов [1–10]. В результате этого кинетостатический анализ механизмов с помощью пакетов прикладных программ является важной частью научной и практической деятельности инженеров и конструкторов. Поэтому программная реализация математических моделей кинетостатического расчета механизмов представляет практический интерес. В качестве языка программирования был выбран Турбо Паскаль фирмы Borland.

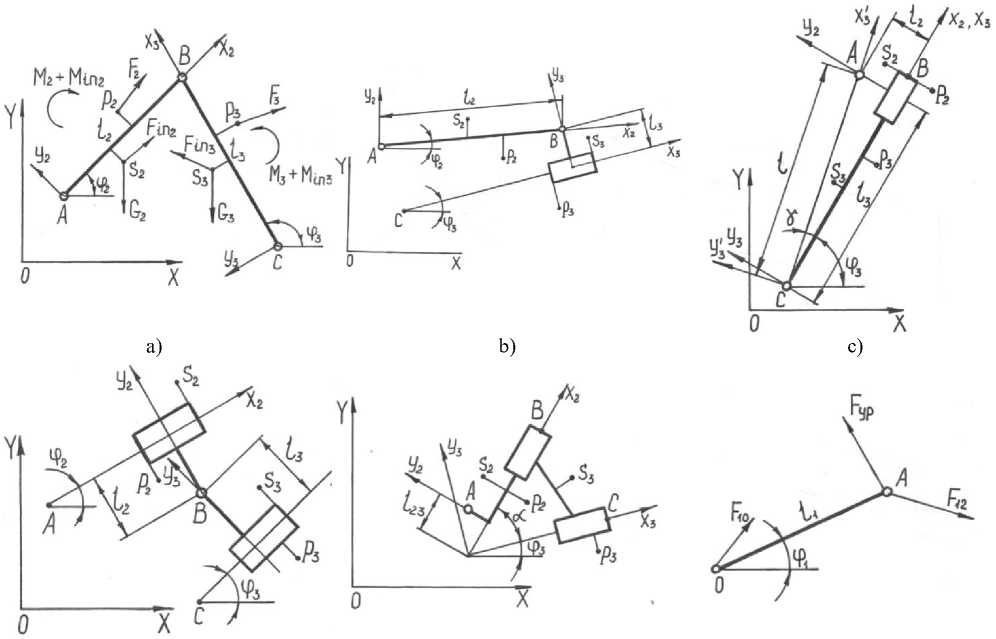
В работе [1] получена математическая модель с процедурами расчета силовых характеристик плоских рычажных механизмов, имеющих в своем составе кроме начального звена хотя бы одну двух поводковую группу Ассура. Расчетные схемы показаны на рисунке 1.

На рисунке 1 приняты следующие обозначения: F 12 - сила, действующая на начальное звено от группы Ассура; F 10 – сила, действующая на начальной звено от стойки; F ур – уравновешивающая сила; l 1 , l 2 , l 3 - длины начального, второго и третьего звеньев; F in2 , M in2 ,F in3 , M in3 – сила инерции и момент от сил инерции на втором и третьем звеньях, соответственно; F 2 , M 2 ,F 3 , M 3 - внешние сила и момент, действующие на втором и третьем звеньях, соответственно; φ 1 , φ 2 ,φ 3 - углы наклона к оси абсцисс начального, второго и третьего звеньев, соответственно; s 2 , s 3 , p 2 , p 3 – центры масс и точки приложения сил соответствующих звеньев.

d)

e)

f)

Рисунок 1. Расчетные схемы двух поводковых групп Ассура: a – первого вида; b – второго вида; c – третьего вида; d – четвертого вида; e – пятого вида; f – ведущее звено

• Figure 1.    Settlement schemes of two flood groups of Assur: a – first look; b – second look; c – third look; d – fourth look; e – fifth look; f – leading link

По результатам работы [1] разработаны компьютерные процедуры, вычисляющие усилия в кинематических парах в группах Ассура и уравновешивающую силу на начальном звене. Перед применением соответствующих вычислительных процедур необходимо знать все внешние силы и моменты, действующие на группу Ассура, а также определить силы инерции и моменты сил инерции. Для их определения, прежде всего, необходимо воспользоваться программным модулем DIADA [2,3], в котором находятся процедуры, вычисляющие кинематические характеристики групп Ассура. Определив таким образом ускорения центров масс звеньев и угловые ускорения звеньев, можно получить информацию о величинах и направлениях сил инерции и моментов сил инерции.

Сам процесс вычислений и построений положений механизма можно представить следующим образом. Организуется цикл, в котором вычисляется положение начального звена механизма. Затем вычисляются положения остальных звеньев механизма путем обращения к соответствующим процедурам модуля DIADA по группам Ассура [2, 3]. Используя графический режим компьютера, выводим на дисплей положение механизма. Вычисляем силы инерции и моменты от сил инерции. Обращаясь к соответствующим процедурам модуля KNTST, вычисляем все усилия в кинематических парах и уравновешивающую силу на начальном звене. В каждой кинематической паре строим силы и их направления при помощи простейших графических процедур. Величины этих сил и их направления выводятся в специальном окне с текстовым режимом. В работе приводятся листинги модуля KNTST и тестовой программы MyTеst, являющейся примером использования вычислительных возможностей разработанного модуля KNTST.

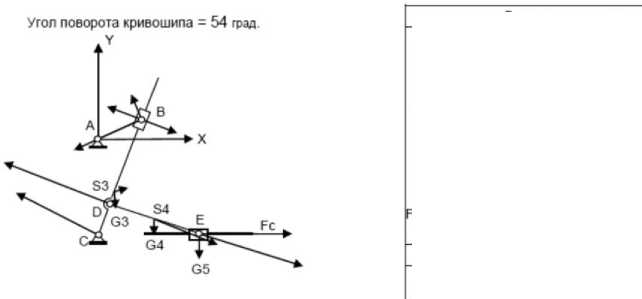
В качестве проверки вычислений процедурами модуля в программе приводится пример вычисления уравновешивающей силы по методу Жуковского (рычаг Жуковского). На рисунке 2 представлен пример работы программы MyTеst.

Фрагмент листинга программы примера расчета механизма1

ProgramMyTest;

{Силовой расчет механизма}

Uses Crt, Graph, Diada, GDiada, Kntst

F_GrText;

Label

Start;

Const g=9.81; n = 360;

writeln('Fin5=', Fin5:12:6, 'Угол =':11>alfafin5*180/pi:5:2);

SetWindow(41,26,80,28,2,'Сила сопротивления', true, false, false);

Writeln('Fc=', Fc:12:6);

ch: = readkey;

if ch = #27 then exit;

if i ≠ n then ClearDevice;

if fi3 < fi3min then begin fi3min: = fi3; ifi3min: = i end;

if fi3 > fi3max then begin fi3max: = fi3; ifi3max: = i end;

end;

if readkey = #27 then exit else goto start;

GraphWriteOff;

FreeMem (p, FileSize(f));

CloseGraph;

writeln('fi3min=', fi3min*180/pi:10:6

ifi3min= ', ifi3min);

writeln('fi3max=', fi3max*180/pi:10:6

ifi3max= ' ifi3max);

readkey;

End. {Main} if ch = #27 then exit else goto start End.

Выход из программы - Esc

Расчетные данные

F50=   98 560347        УГОЛ= 270.00 Нх5=   0.00000 F45=  1159.606853        УГОЛ= 342 75 F43"  1231.704974         УГОЛ= 159.17 F30=  970.691007        УГОП= 153.98 F32=  400.430211        УГОЛ= 159.21 НхЗ=   0.00000 F21=  400.430211        УГОЛ= 159.21 F10=  284.204048        Угол= 204.00 Fyp=   282.005825        Угол= 114.00 Рур1=   282 0 05825        Рычаг Жуковского

Силы инерции и моменты

Fin3=   96.967168        УГОЛ= 10.18 Момент от сил инерции= -16.629837 Fin4=   43.945234        Угол= 5.22 Момент от сил инерции= - 0.201592 Нп5=  10 7 945234       УГОЛ= 360.00

Сила сопротивления

Fc= 1000 00000

Рисунок 2. Пример работы программы MyTest

• Figure 2.    Example of work of the program MyTest

Использование библиотечных процедур модуля KNTST, позволяет сравнительно просто организовать имитацию движения механизма, рассчитать реакции в кинематических парах, вычислить уравновешивающую силу и построить план сил в каждом положении механизма. Если необходимо значения силовых характеристик можно вывести на дисплей. Такой подход обеспечивает эффективность при проведении кинетостатического расчета механизма на основе технического задания.