Программная реализация метода Гаусса-Жордана для решения систем уравнений
Автор: Григоренко В.Е., Цейтлина Н.Е., Игрунова С.В.
Журнал: Экономика и социум @ekonomika-socium
Статья в выпуске: 5-1 (18), 2015 года.
Бесплатный доступ
В данной статье описана программа, решающая квадратные системы линейных алгебраических уравнений методом Гаусса - Жордана.
Программная реализация, метод гаусса - жордана, система линейных алгебраических уравнений, матрицы, линейная алгебра
Короткий адрес: https://sciup.org/140114395
IDR: 140114395
Текст научной статьи Программная реализация метода Гаусса-Жордана для решения систем уравнений
Решение систем квадратных уравнений бывает затруднительно, в отдельных случаях такие системы можно решить, используя способы подстановки или сложения. Объектом исследования данной работы являются квадратные системы линейных уравнений, решение предлагается выполнить методом Гаусса – Жордана [1].
В данной работе представлено описание процесса разработки приложения в среде Microsoft Visual Studio 2010 [2] для поставленной задачи, программа выполнена как приложение Windows Forms [3].
Рассмотрим основные функции, применяемые при разработке. Основной функцией является button1_Click, вызываемая при нажатии на “OK”. В ней определяются основные изменения внешнего вида программы, связанные с расчетами. Вызываются функции form или typing в зависимости от выбранного варианта заполнения матрицы коэффициентов. После вызова одной из функций заполнения значений коэффициентов и столбца свободных членов, вызывается функция show, а за ней функция vector.
В функции form происходит заполнение матрицы случайными числами. Функция typing заполняет двумерный массив значениями, введенными с клавиатуры. Функция clear очищает обе таблицы от имеющихся значений. Функция show выводит на экран значения коэффициентов и столбца свободных членов. Заголовочной ячейке последнего столбца присваивается значение “Столбец свободных членов”, верхней левой заголовочной ячейке присваивается значение “Коэффициенты”, в оставшихся заголовочных ячейках строк и столбцов выводятся их порядковые номера, начиная с единицы, в самих ячейках таблицы отображаются соответствующие значения двумерного массива, передаваемого как параметр.
Функция vector осуществляет расчет корней системы уравнений и выводит их на экран. В ней вызывается функция gauss, рассчитывающая корни системы уравнений. Затем выводится нумерация столбцов с единицы в заголовочных ячейках, в самой строке выводятся значения массива корней системы. В теле функции gauss вызывается функция triangular, затем вызывается функция upend, затем снова вызывается функция triangular, далее вызывается функция one_for_diagonal, последней вызывается функция calculate_result.
Функция triangular выполняет приведение матрицы к треугольному виду. Данный метод реализован с помощью программного кода:
private: void triangular(double** arr, int x)
{ double a;
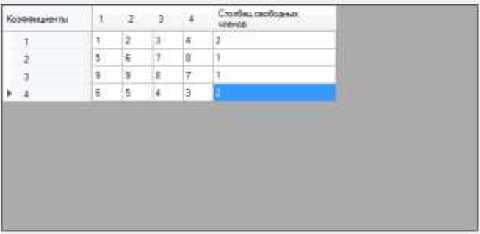
for(int i=0; i for(int m=i+1; m { a=(-1)*arr[m][i]/arr[i][i]; for(int j=0; j { arr[m][j]+=arr[i][j]*a; } }} Функция upend переворачивает сверху вниз все строки матрицы, а затем меняет порядок всех столбцов, наоборот, за исключением последнего столбца – столбца свободных членов. В ее теле вызывается функция equating, присваивающая значения одной матрицы другой, затем вызывается функция upend_strokes, переворачивающая строки, далее снова вызывается функция equating, далее вызывается функция upend_columns, переворачивающая столбцы. Функция one_for_diagonal производит деление всех элементов каждой строки на значение элемента, находящегося в данной строке на главной диагонали. Функция calculate_result присваивает значения столбца свободных членов одномерному массиву, также передаваемому как параметр. Так как изменялся порядок столбцов, то значения последнего столбца двумерного массива присваиваются, начиная с последнего. Пользователь не должен изменять значения коэффициентов и столбца свободных членов при заполнении случайными числами, должна быть возможность ввода значений при заполнении вручную. Для этого также должны быть написаны специальные функции. Для проверки вводимого значения для события окончания ввода значения следует написать функцию, которая при вводе в ячейку таблицы значения, не являющегося числом, вызывается сообщение об ошибке и значение изменяется на нуль. Результаты работы программы: Рисунок 1 – Результат работы программы при заполнении случайными числами £ “*411 Хэдм Гци С**Ч»рв11** Mtpmo Очаоиш О ярмэмма* Вии Рисунок 2 – Результат работы программы в том случае, когда система несовместна Практическая значимость полученных результатов заключается в возможности получения универсальной программы для решения квадратных систем линейных алгебраических уравнений, имея только начальные значения коэффициентов уравнения, начальные значения свободных членов, а также количество переменных, значения которых необходимо найти. Разработанная программа освобождает пользователя от необходимости вручную проводить расчеты. Учитывая, что значения, используемые как коэффициенты и свободные члены могут быть неудобны для использования в расчетах, но необходимы для получения верного результата, данная программа имеет практическую значимость. Пути дальнейшего совершенствования программы: получение более подробной справки по программе, не выходя из приложения; возможность просмотра точного решения системы уравнений, при необходимости; более детальная обработка исключительных ситуаций.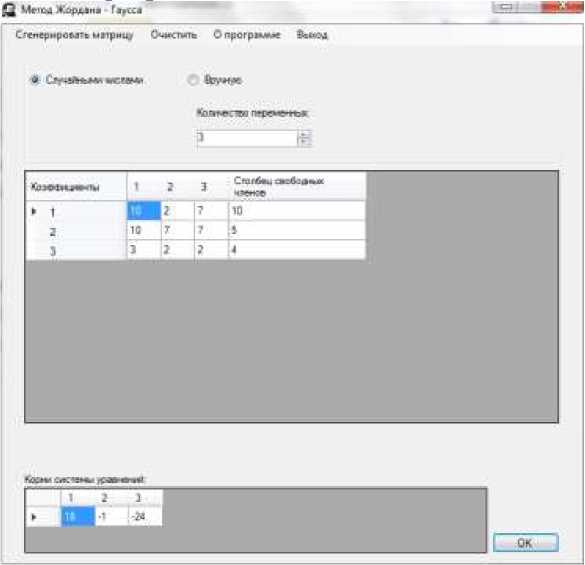



Список литературы Программная реализация метода Гаусса-Жордана для решения систем уравнений
- Системы линейных алгебраических уравнений | mathhelpplanet.com -Режим доступа http://mathhelpplanet.com/static.php?p=sistemy-linyeinykh-algebraicheskikh-uravnenii, свободный.
- Visual Studio 2010 | msdn.microsoft.com -Режим доступа https://msdn.microsoft.com/en-us/library/dd831853(v=vs.100).aspx, свободный.
- Windows Forms | msdn.microsoft.com -Режим доступа https://msdn.microsoft.com/ru-ru/library/dd30h2yb(v=vs.110).aspx, свободный.


