Программная реализация нахождения периметра и площади фигуры с помощью аппроксимации
Автор: Бабенко Александр Андреевич, Бабенко Анастасия Александровна
Журнал: Форум молодых ученых @forum-nauka
Статья в выпуске: 7 (59), 2021 года.
Бесплатный доступ
В статье реализована программа нахождения периметра и площади с использованием аппроксимации. Для аппроксимации заданной фигуры был использован алгоритм Дугласа-Пекера.
Аппроксимация, алгоритм дугласа-пекера, формула площади гаусса, с++
Короткий адрес: https://sciup.org/140288820
IDR: 140288820
Текст научной статьи Программная реализация нахождения периметра и площади фигуры с помощью аппроксимации
Для аппроксимации заданной фигуры был использован алгоритм Дугласа-Пекера. Алгоритм Дугласа-Пекера — это алгоритм, позволяющий уменьшить число точек кривой, аппроксимированной большей серией точек. Суть алгоритма состоит в том, чтобы по данной ломаной, аппроксимирующей кривую, построить ломаную с меньшим числом точек. Алгоритм определяет расхождение, которое вычисляется по максимальному расстоянию между исходной и упрощённой кривыми. Упрощенная кривая состоит из подмножества точек, которые определяются из исходной кривой. Для нахождения периметра фигура разбивалась на отрезки, и вычислялись их длины с помощью расстояния Евклида между двумя точками. Существующие множество методов нахождения площади, но для конкретной задачи будут использоваться два следующих метода: формула площади Гаусса и нахождение площади по подобию многоугольников. Для написания программы была выбрана среда программирования Visual Studio 2019 C++, основанная на языке программирования C++. Данная среда выгодно отличается эффективностью и надежностью
Программная реализация нахождения периметра и площади с использованием аппроксимации:
-
1 .Нахождения максимального расстояния
double mag = pow(pow(dx, 2.0) + pow(dy, 2.0), 0.5);
double pvdot = dx * pvx + dy * pvy; double dsx = pvdot * dx;
double dsy = pvdot * dy;//Вычесть его из pv double ax = pvx - dsx; double ay = pvy - dsy; return pow(pow(ax, 2.0) + pow(ay, 2.0), 0.5); } double dmax = 0.0;
size_t index = 0;
for (size_t i = 1; i < end; i++) { double d = calculateDistance(pointList[i], pointList[0], pointList[end]);
if (d > dmax) { index = i; dmax = d;} }
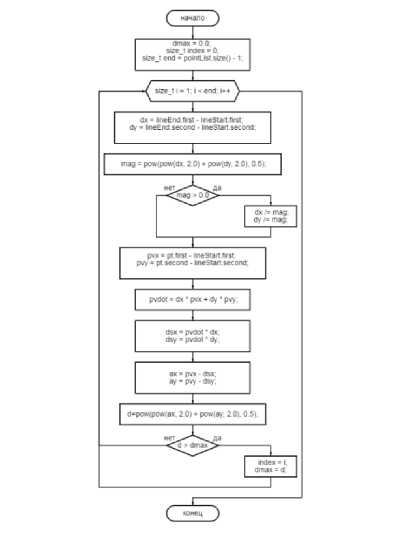
Рисунок 1 - Блок схема нахождения максимального расстояния
2. Алгоритм аппроксимации методом Дугласа-Пекера
Листинг кода на C++ алгоритма Дугласа-Пекера:
if (dmax > epsilon) {
//Если максимальное расстояние больше ε, упростить кривую vector
mainAlgorithm(firstLine, epsilon, recResults1); mainAlgorithm(lastLine, epsilon, recResults2);
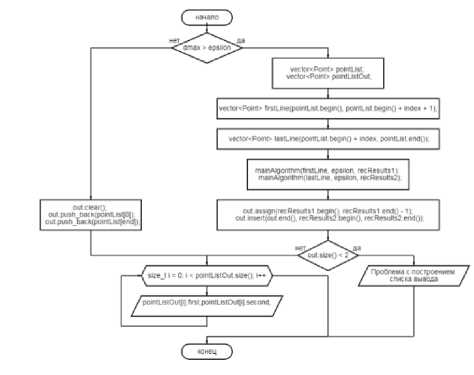
Рисунок 2 - Блок схема алгоритма Дугласа-Пекера
3. Нахождение я периметра и площади
P1 += sqrt(pow((pointList1[i + 1].first - pointList1[i].first), 2.0) + pow((pointList1[i + 1].second - pointList1[i].second), 2.0));
S1 += 0.5 * abs(pointList1[i].first * pointList1[i + 1].second - pointList1[i + 1].first * pointList1[i].second);} else{
P1 += sqrt(pow((pointList1[0].first - pointList1[i].first), 2.0) + pow((pointList1[0].second -pointList1[i].second), 2.0));
S1 += 0.5 * abs(pointList1[i].first * pointList1[0].second - pointList1[0].first *
P2 += sqrt(pow((pointListOut[i + 1].first - pointListOut[i].first), 2.0) + pow((pointListOut[i + 1].second - pointListOut[i].second), 2.0));} else{
P2 += sqrt(pow((pointListOut[0].first - pointListOut[i].first), 2.0) + pow((pointListOut[0].second - pointListOut[i].second), 2.0));}}
S2 = S1 * pow(P2,2.0) / pow(P1,2.0);
cout « "Периметр P1 = " « P1 « endl;
cout « "Периметр P2 = " « P2 « endl;
cout « "Площадь S1 = " « S1 « endl;
cout « "Площадь S2 = " « S2 « endl;
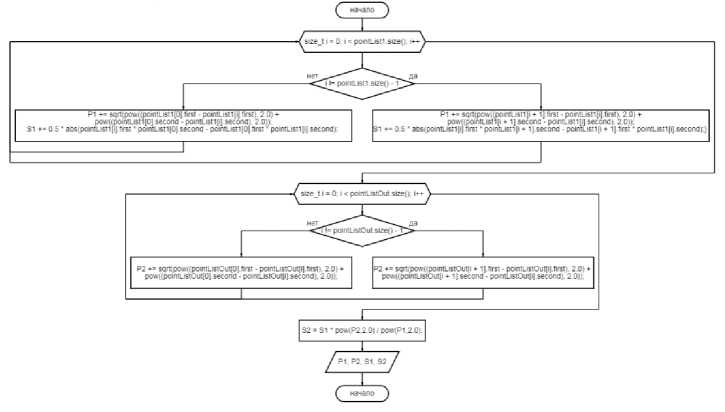
Рисунок 3 - Блок нахождения периметра и площади Тестирование алгоритма Дугласа-Пекера
Фигура для аппроксимации представлена на рис. 4.
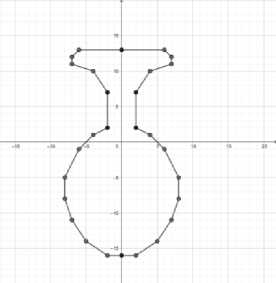
Рис. 4. Входное изображение
Периметр и площадь фигуры при ε=0,5, рис.5.
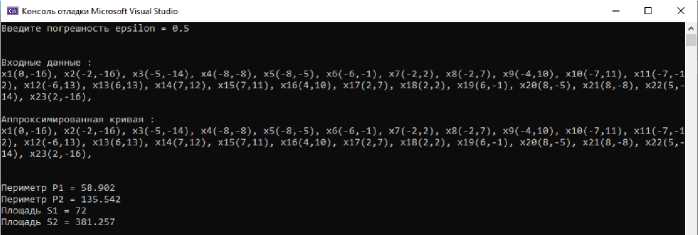
Рисунок 5 - Периметр и площадь фигуры при ε=0,5
Периметр и площадь фигуры при ε=2, рис.6.
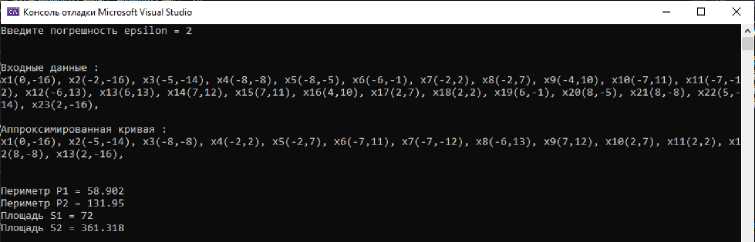
Рисунок 6 - Периметр и площадь фигуры при ε=2
Фигура после аппроксимации с ε=0,5 представлена на рис. 23.
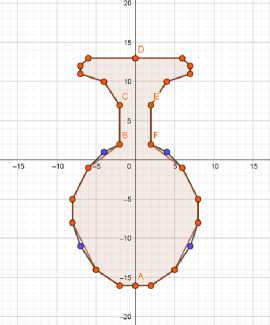
Список литературы Программная реализация нахождения периметра и площади фигуры с помощью аппроксимации
- Дейтел Х.М. Как программировать на С++: Пятое издание / Х.М. Дейтел, - С.Пб. ООО "Бином-Пресс", 2011. - 1456 с.
- Понарин Я.П. Элементарная геометрия. Том 1. Планиметрия, преобразования плоскости / Я.П. Понарин, - М.: МЦНМО, 2004. - 312 с.
- Семина Е.В. Основы алгоритмизации и структурного программирования на C++: учебно-методическое пособие / Е.В. Семина, А.В. Артемов, - Орел, 2014. - 48 с.


