Программная реализация нечеткой логики с лингвистическими переменными

Zagibin N., Ulyanov S. Software implementation of fuzzy logic with linguistic variables. System Analysis in Science and Education, 2021;(1):45–57(In Russ). Available from:

Сегодня развитие технологии в области имитирования процессов интеллектуальной деятельности головного мозга человека достигло невиданных возможностей. Распознавание лиц, обработка больших данных, создание роботов с системой обучения и адаптации к реальности, интеллектуальное управление процессами производства и систем автоматического регулирования – это лишь малый список достижений результатов эволюции научной деятельности в области интеллектуальных технологий. Помимо всего прочего данные технологии позволяют убрать из систем управления человеческий фактор и медленную скорость адаптации в меняющихся, а также критических ситуациях. Это в большей мере играет роль в управлении такими объектами как атомные электростанции или системы управления космическими аппаратами. Тем не менее мы можем видеть, как в повседневную жизнь вместе с умной техникой происходит внедрение интеллектуальной технологии, которая позволяет оптимизировать повседневные процессы и достигать поставленные цели за меньшее время несмотря на непредвиденные ситуации.

«Интеллектуализацию» в представленной технологии представляют множество вычислений, состоящих в общем виде из: мягких вычисления; эволюционного программирования; генетических алгоритмов и алгоритмов оптимизации типа иммунных алгоритмов; алгоритмов оптимизации на основе поведенческих реакций и обмена информацией активных агентов (самоорганизация целенаправленного и оптимального поведения в условиях «толпы»); квантовых генетических алгоритмов для глобальной оптимизации; квантовых нейронных сетей обучения и мн. др. [1]. В большинстве случаев для реализации автоматического управления прибегают к использованию ПИД (пропорционально интегрально-дифференциального) регулятора. Данная система управления составляет нижний (исполнительный) уровень с обратной связью в иерархии системы интеллектуального управления. В обычной системе с ПИД регулированием коэффициенты самого регулятора динамически не изменяются и не корректируются под внешние возмущения, их задают статически при создании системы. Для гибкой работы данной системы управления применяют нечеткий регулятор (НР) базирующийся на работе нечетких систем с нечеткой логикой (рис. 1) [2]. Данная логика позволяет приблизиться к модели процесса размышления человека при помощи лингвистических переменных и сделать соответствующие выводы на основании функций принадлежности в рассматриваемом классе понятий. Это позволит внедрить даже субъективные знания об объекте управления, которые впоследствии обработки вывода нечеткой логики обратятся в четкие значения для регулирования объектом управления.

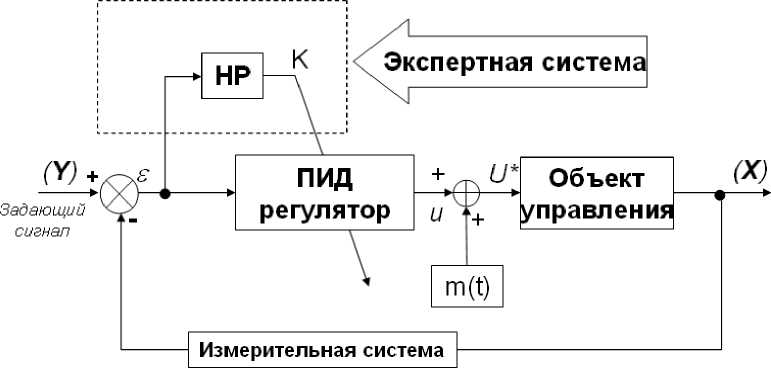
Рис. 1. Структура ИСУ первого поколения [1]

1.    Актуальность

Потребность в сохранении ресурсов и извлечении большей экономической выгоды от использования и производства продукции сейчас как никогда раньше стоит перед человечеством в 21 веке. Еще в годы промышленной революции в большинстве случаев человеческий труд заменялся на машинный, сокращая время на производство. С приходом прогресса в электронной промышленности стало упрощаться и управление машин, где человек посредством заданных алгоритмов планировал их действие. Но сложность систем управления вместе со сложностью агрегатов возросла и как следствие в большинстве случаев стало невозможно описать динамическую модель объекта, откуда начали возникать непредвиденные ситуации управления и аварии. Для решения описанной проблемы достижения в непредвиденных ситуациях цели управления, адаптации в реальных условиях и самообучению применяется интеллектуальная система управления. Помимо управления данная система также позволяет снизить расход полезных ресурсов на исполнительном уровне. Как итог применения такой системы позволило добиться высокого уровня управления и экономической выгоды в отличии от их классических аналогов.

Для создания базы интеллектуальной систем управления (ИСУ), а также реализаций логических заключений имитируемые человеческое мышление (как пример нечеткое человеческое суждение «да нет, наверное») необходимы нечеткие системы. Нечеткие системы позволяют формировать базу нечетких логических заключений (базу знаний), используемую для обработки ввода и формирования управляющих (выходных) значений (как например управление ПИД-регулятором), как самой интеллектуальной системе, так и человеку эксперту, реализующему заданные принципы управления объектом [2]. В этом смысле нечеткий регулятор в интеллектуальном управлении является базовым элементом, в котором существует множество правил вывода объединённых в базу знаний, которая в последствии самоадаптируется за счет надстроечных элементов ИСУ для работы объекта управления (ОУ) в непредвиденных условиях. Но все это невозможно было бы представить без нечеткой логики, которая манипулирует нечеткими множествами сформированные в лингвистических переменных.

Программная реализация в виде подключаемой библиотеки позволит разработчикам создать свою базу знания нечеткой логики или нечеткие логические конструкции из нечетких множеств для проектов, направленных на моделирование человеческого умозаключения или разработки ИСУ.

2. Теоретическое представление лингвистической переменной и нечеткой логики

Лингвистическая переменная

Основой лингвистической переменной является нечеткое множество (понятие, введенное Л. Заде).

Определение [1]: нечеткое множество ( a fuzzy set )

Пусть X есть некоторое универсальное множество (универсум). Тогда нечеткое множество А в X определяется как упорядоченное множество пар

Л = {(х, jU(x))|x 6 X}, где ^ (x) е [0,1] называется функцией принадлежности (ФП) элемента х к нечеткому множеству А.

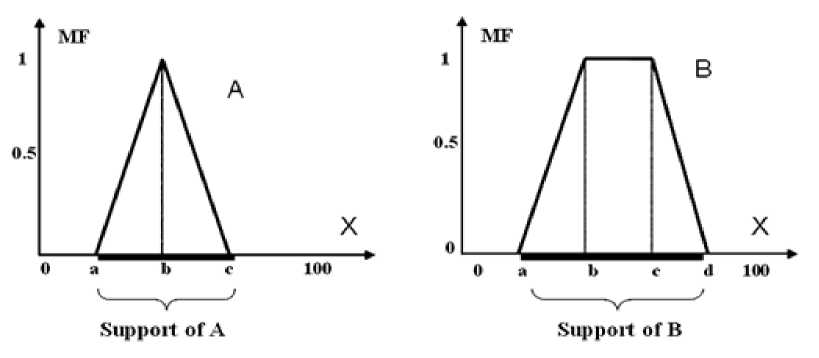
Рис. 2. Примеры нечетких множеств [1]

Определение [1]: лингвистическая переменная (ЛП) представляет собой следующую пятерку (X , T ( X ), X , G , М^ , где X — имя переменной, T ( X ) — терм-множество, задающее множество значений ЛП, являющихся языковыми выражениями (синтагмами), X - универсум, G - синтаксическое правило, используя которое мы можем формировать синтагмы A,B ,... е T ( X ) , M — семантическое правило, используя которое каждой синтагме A е T ( X ) приписывается ее значение, являющееся нечетким множеством в универсуме X .

Приближенно можно сказать, что набор нечетких множеств, определенных на заданном универсуме X и принадлежащих логически к одному и тому же классу, является лингвистической переменной.

Нечеткие логические операции

Определение [1]: нечеткая конъюнкция ( Fuzzy conjunction или fuzzy AND ).

Значение истинности нечеткой конъюнкции A л B определяется следующим образом:

ВамАХ = тт^х),!^)), где ^ (x), ^ (x) - значения истинности нечетких предикатов А, В соответственно.

Определение [1]: нечеткая дизъюнкция ( Fuzzy disjunction или fuzzy OR ). Значение истинности нечеткой конъюнкции A v B определяется следующим образом:

ЦаувЮ = тах(цА(х),цв(х)), где ^ (x), ^ (x) - значения истинности нечетких предикатов А, В соответственно.

Определение [1]: нечеткое отрицание ( Fuzzy negation ). Значение истинности нечеткого отрицания A определяется следующим образом:

Н-А(х) = 1 -ЦаМ, где ^ (x) - значение истинности нечеткого предиката А.

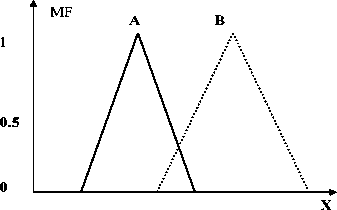
_MF        A OR B

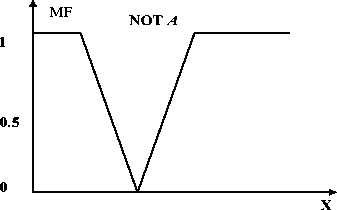
MF

X

0.5

A AND B

X

Рис. 3. Примеры нечетких операций над нечеткими множествами [1]

Нечеткая логика

Нечеткая логика базируется на выше приведённых логических операциях, построения правил и вывода из них .

Определение [1]: нечеткая импликация или нечеткое правило (Fuzzy implication или a fuzzy rule) представляет собой следующее выражение:

ЕСЛИ x есть A , ТО y есть B , где Α и Β – лингвистические переменные, определенные нечеткими множествами на универсумах Χ и Υ соответственно. В символьной форме запись имеет следующий вид: R =A →B .

Часть «ЕСЛИ» ( х есть Α ) называется антецедентом ( the antecedent ) или посылкой. Часть «ТО» ( y есть B ) называется следствием ( consequence ) или заключением.

Определение [1]: Нечеткая импликация (Fuzzy implication). Значение истинности нечеткой импликации A → B определяется следующим образом:

Ца^в (х) = Ца (х) л Цв (х) , где л есть операция нечеткой конъюнкции (fuzzy AND operation) и ^ (x), ^ (x) - значения истинности нечетких предикатов A, B соответственно.

Нечеткий вывод, основанный на правиле max- min композиции

Такого типа вывод строится как «усечение» следствия от минимума из максимумов нечеткой конъюнкции посылок.

Рассмотрим следующий нечеткий вывод [1]:

Посылка 1 ( нечеткий вход): x есть A ′

Нечеткое правило: ЕСЛИ x есть A , ТО y есть B

Нечеткое заключение: y есть B ′

Формула называется max-min композицией (max-min composition).

Цв'(У) = таатт^хШх.у) ] = ^л'ЮЛдяСг,)/) ].

X

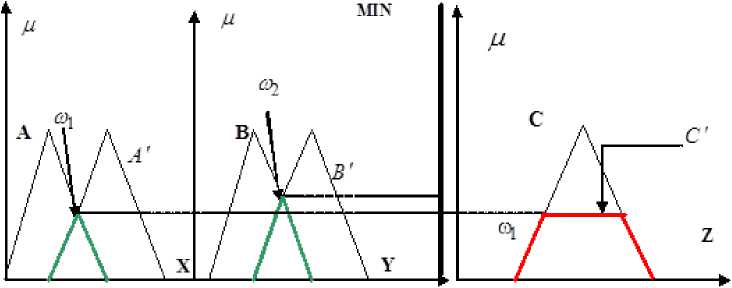
Рис. 4. Графическая интерпретация схемы нечеткого вывода на основе max-min композиции [1]

Нечеткая Модель Мамдани

В общем виде, четкое выходное значение в нечеткой модели Мамдани вычисляется по следующей формуле и вычисляется как дизъюнкция «усечений» следствий, построенных от минимального значения функции пригодности посылок правил:

f(xi.

^х4 )

Й=1У'ПМ,СгР $Мх.)

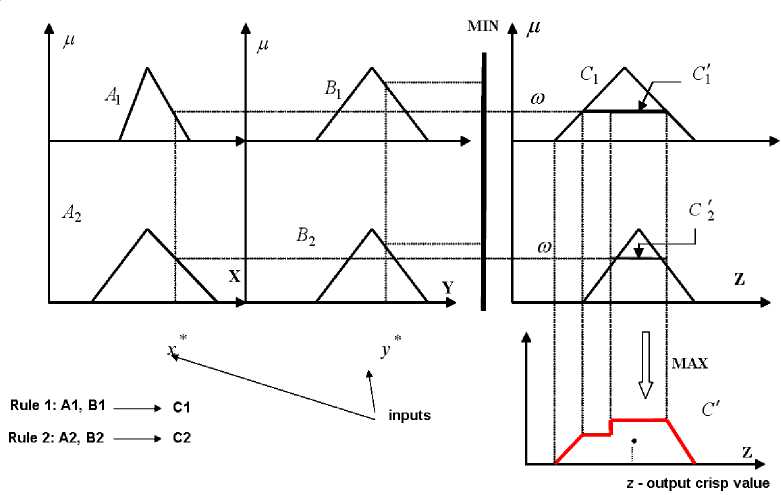
Рис. 5. Графическое представление нечеткого вывода в Мамдани модели [1]

Нечеткая Модель Сугено

В модели Сугено вывод определяется функцией от входных значений, где каждому правилу в соответствии ставится функция принимающая входные переменные и результатом модели считается сумма произведений данных функций, умноженных на минимальные значения функции пригодности посылок от выходных значений (активация правила) поделенная на сумму всех активаций правил.

^(^ 1 ,^ 2 ,

, ^— n )

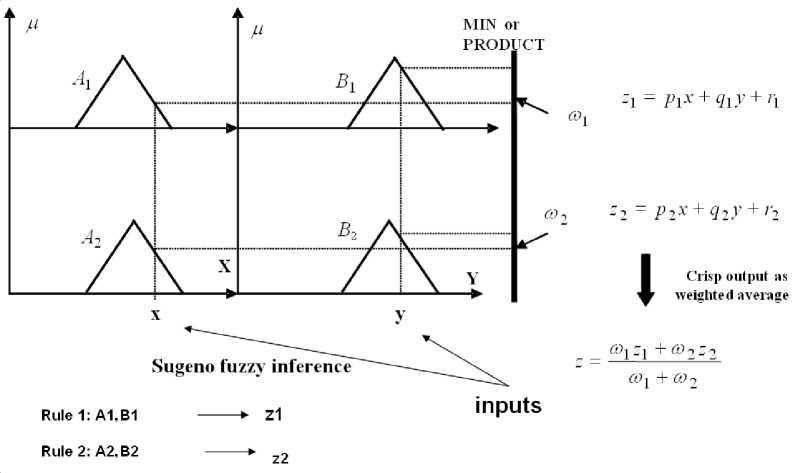
Рис. 6. Графическое представление нечеткого вывода в Сугено модели [1]

Нечеткая Модель Цукамото

В отличии от вышеперечисленных моделей нечеткого вывода в модели Цукамото используются следствии правил в виде монотонно убывающей или монотонно возрастающей функции пригодности нечеткого множества из которых находят значения аргумента данной функции по минимуму значения функции пригодности посылок (активация правил) и суммируя перемножения этих найденных двух значений делят на сумму активаций правил.

F(x1,

Лп)

5{'1Z-n?-1#<},(xl) Е^ПМ^)

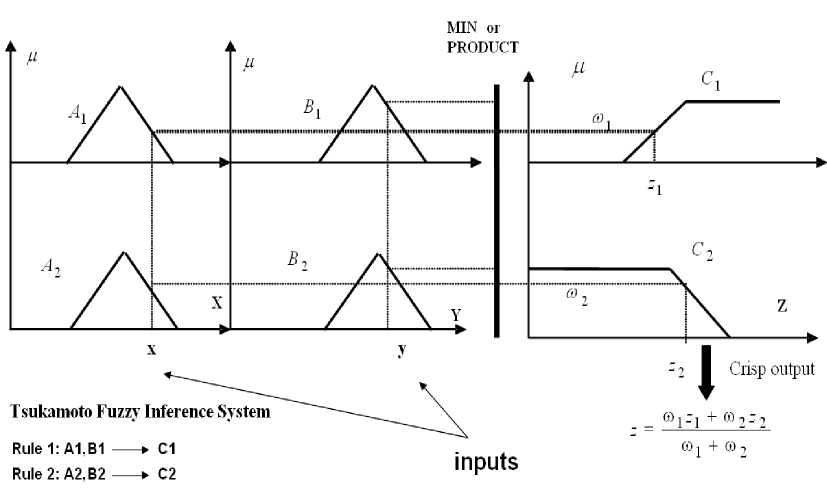
Рис. 7. Графическое представление нечеткого вывода в Цукамото модели [1]

3.    Программная реализация лингвистических переменных и нечеткой логики

Программная реализация представляет собой два класса: Linguistic_variable и Fuzzy_inference (рис. 8), написанных на языке программирования C++ .

Linguistic_variable – это класс создающий объекты лингвистических переменных, в основе которого лежит контейнер нечетких множеств fuzzy_set с их синтагмами (наименованиями). Его методы составляют основу нечетких логических операций (нечеткая конъюнкция, нечеткая дизъюнкция и нечеткое отрицание), добавление по точкам отрезков нечетких множеств и «отрисовку» данных множеств на элементе chart WindowsForm .

Fuzzy_inference – класс нечеткого вывода наследуемый от класса Linguistic_variable , реализующий в себе методы нечеткого вывода, основанный на правиле max-min композиции, нечеткие модели Мамдани, Сугено и Цукамото.

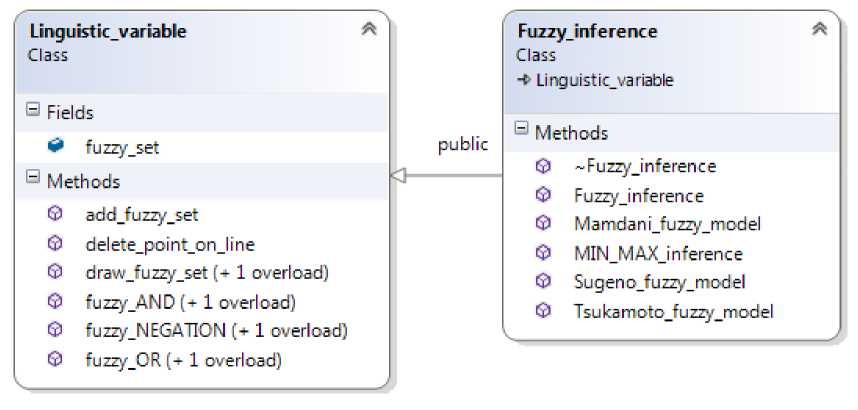
Рис. 8. Классы, составляющие нечеткую систему

Linguistic_variable fuzzy_set в программой реализации представляет собой стандартный контейнер: map>, где ключом представляется одно из терм множеств (наименование нечеткого множества) лингвистической переменной, а ключом внутреннего map является значение x из заданного набора нечеткого множества A в области универсального множества X. Значение ключа внутреннего map представляет функция пригодности ^ (x) е [0,1].

Чтобы не добавлять в нечеткое множество по одной точке в методе add_fuzzy_set можно указать наименование множества и указать необходимые точки:

Ling_var.add_fuzzy_set (" young ", { { 0, 1 }, { 40, 1 }, { 60, 0 } });

Для наглядного отображения на диаграмме потребуется всего лишь в методе draw_fuzzy_set перечислить интересующие наименования нечетких множеств:

Ling_var.draw_fuzzy_set ( chart1 , { " young ", " old ", " old2 " });

fuzzy_AND принимает только два аргумента указывающих на множества и строит новое нечеткое множество на основе их нечеткой конъюнкции за счет вычисления пересечения прямых от двух точек и сравнения точки одного множества с её значением функции прямой от двух точек другого множества (рис. 9).

fuzzy_OR принимает также только два аргумента указывающих на множества и строит новое нечеткое множество на основе их нечеткой дизъюнкции за счет вычисления пересечения прямых от двух точек и сравнения точки одного множества с её значением функции прямой от двух точек другого множества (рис. 9).

fuzzy_OR принимает один аргумент указывающий на множество и строит новое нечеткое множество на основе нечеткого отрицания за счет вычитания из единицы функции принадлежности каждого аргумента нечеткого множества (рис. 9).

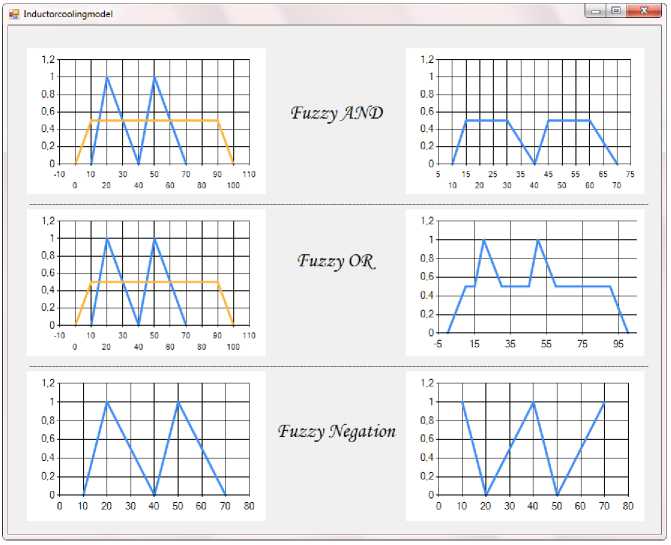
Рис. 9. Результаты нечетких логических операций

Fuzzy_inference

Чтобы использовать нечеткие логические операции и создавать собственные контейнеры для результатов было использовано наследование от класса Linguistic_variable. Здесь в аргументах функций используются двухмерные конструкции инициализаций правил где в обязательном порядке (кроме модели Cугено) необходимо чтобы количество «входных данных» было на 1 меньше количества перечисляемых посылок со следствием (т.к. они объединены). Как например вызов функции нечеткой модели Мамдани:

A_inference.Mamdani_fuzzy_model ({28,      38},      {{& Ling_var.fuzzy_set [" young "],

&Ling_var.fuzzy_set[" old "],    &Ling_var.fuzzy_set[" old2 "]},    {&Ling_var.fuzzy_set[" old3 "],

&Ling_var.fuzzy_set[" old4 "], &Ling_var.fuzzy_set[" old5 "] } });

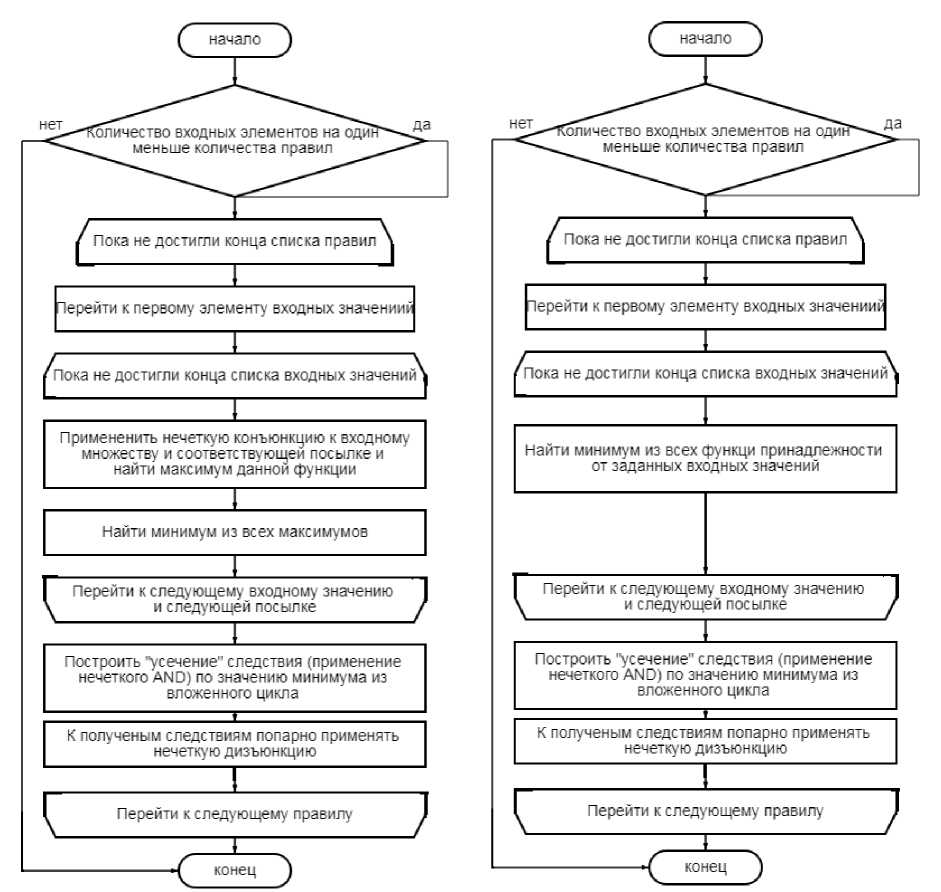
MIN_MAX_inference – вывод max-min композиции реализует следующий алгоритм вывода, изображенный на рис. 10 .

В модели Мамдани ( Mamdani_fuzzy_model ) входными данными являются значения x универсального множества лингвистической переменной. Алгоритм вывода приведен выше на рис. 10.

юличество входных элементов на оди! меньше количества правил начало начало

^«-■'■пСоличество входных элементов на оди1 меньше количества правил

Пока не достигли конца списка входных значений

Примененить нечеткую конъюнкцию к входному множеству и соответствующей посылке и " найти максимум данной функции

Перейти к следующему входному значению и следующей посылке

Перейти к следующему правилу

Пока не достигли конца списка правил

Пока не достигли конца списка входных значений

Перейти к следующему входному значению и следующей посылке

Перейти к следующему правилу

^ конец нет конец

Построить "усечение" следствия (применение нечеткого AND) по значению минимума из вложенного цикла

*                           ---------

К полученым следствиям попарно применять нечеткую дизъюнкцию

Построить "усечение" следствия (применение нечеткого AND) по значению минимума из вложенного цикла

t

К полученым следствиям попарно применять нечеткую дизъюнкцию

Найти минимум из всех функци принадлежности от заданных входных значений

Найти минимум из всех максимумов

Перейти к первому элементу входных значении^

Пока не достигли конца списка правил

Перейти к первому элементу входных значениий

Рис. 10. Алгоритм вывода max-min композиции(слева) и алгоритм модели Мамдани (справа)

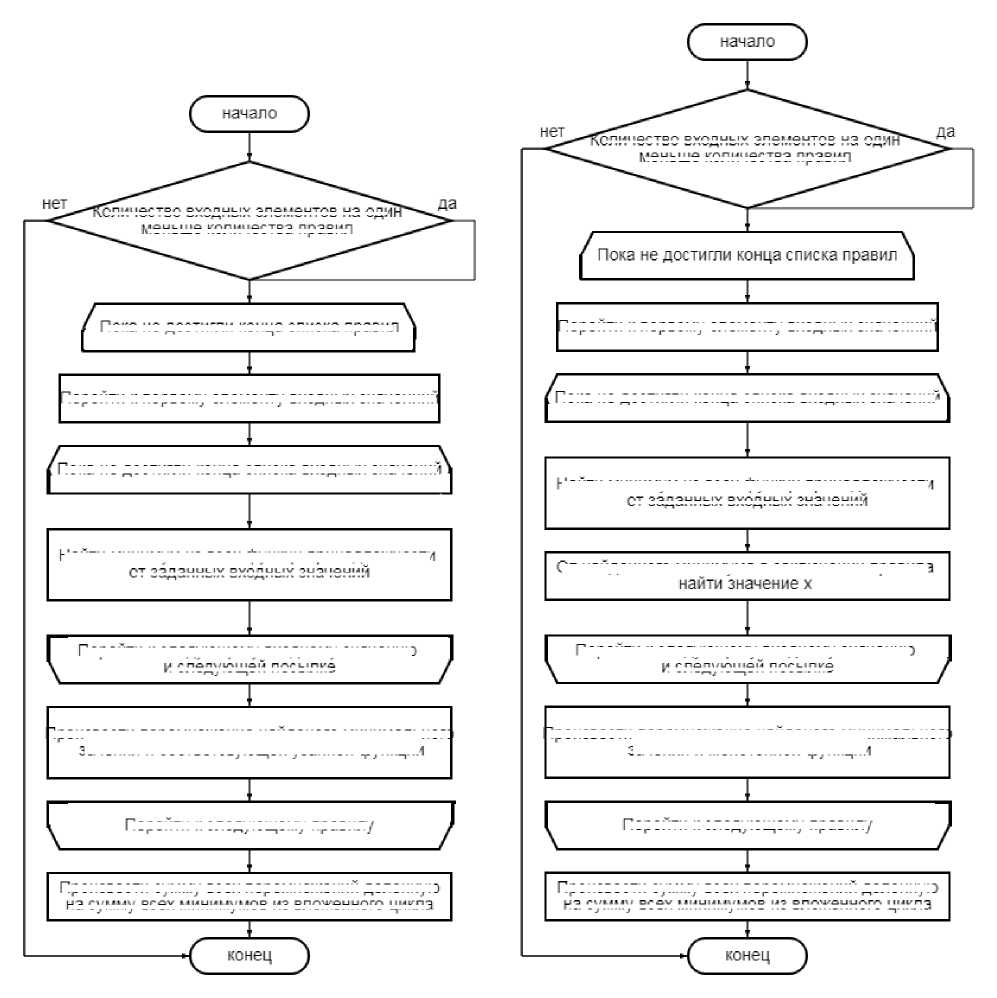
В модели Сугено ( Sugeno_fuzzy_model ) в качестве вывода используются сопоставленные в соответствие с правилами заданные функции, поэтому алгоритм теперь накапливает за циклические проходы сумму произведения минимальных значений на соответствующую функцию после чего в конце производится деление на сумму всех минимальных значений, где следующий алгоритм на рис. 11 отображает это.

В модели Цукамото ( TsukamotoJuzzymodel ) вместо двух первых моделей вывода используется монотонно возрастающая или монотонно убывающая функция пригодности в качестве следствия поэтому её алгоритм приобретает следующий вид (рис. 11).

пока не достигли конца списка правил

Произвести перемножение наиденого минимальной зачения и монотонной функции на сумму всех минимумов из вложенного цикла на сумму всех минимумов из вложенного цикла оличество входных элементов на оди меньше количества правил оличество входных элементов на оди меньше количества правил

Рис. 11. Алгоритм модели Сугено (слева) и алгоритм модели Цукамото (справа)

Перейти к первому элементу входных значении^

Перейти к первому элементу входных значении^

Пока не достигли конца списка входных значении

Наити минимум из всех функци принадлежности

от заданных входных значении

Перейти к следующему входному значению

и следующей посылке

Троизвести перемножение наиденого минимальное зачения и соответсвующей узанной функции

Перейти к следующему правилу

Произвести сумму всех перемножении деленную

Пока не достигли конца списка входных значении

Наити минимум из всех функци принадлежности

от заданных входных значении

От найденного минимума в заключении правила

Перейти к следующему входному значению

и следующей посылке

Перейти к следующему правилу

Произвести сумму всех перемножении деленную

Заключение

Без интеллектуальных технологий невозможно было бы представить развитие робототехники, систем автоматического управления и искусственного интеллекта применяемые в многочисленных отраслях общества, все это дает качественно новый подход к проектированию и созданию экономически привлекательных инструментов для управления процессами производства, техническими комплексами и машинами рационально перераспределяя и используя полезные ресурсы. Для реализации такого рода технологий необходимы средства, поддерживающие построение фундаментальных знаний об управляемом объекте. Таким образом в качестве начального базиса в области разработки интеллектуальных систем управления были разработаны классы поддерживающие нечеткие вычисления и нечеткую логику с помощью которых впоследствии можно проектировать базы знаний, гарантирующие достижения поставленных целей управления.