Программно-реализованная имитационная модель массового обслуживания общего вида

Математические методы теории массового обслуживания обеспечивают возможность решения многочисленных задач расчета характеристик качества функционирования различных компонент компьютерных сетей. Сюда входят оценки вероятностно-временных характеристик узлов коммутации и маршрутизации; анализ производительности локальных сетей и сетей с множественным доступом; анализ буферной памяти узлов и методов локального и глобального управления потоками; расчета потерь и загрузки линий связи.

В данной работе узел сети представлен в виде m -канальной системы массового обслуживания (СМО) GI / G / m / k как без ограничений на длину очереди, так и с потерями. Разработан алгоритм работы имитационной модели такой СМО на основе дискретно-событийного подхода (списков событий), приведены расчеты её основных характеристик в зависимости от загрузки, коэффициентов вариаций распределений входного потока и времени обслуживания.

Структура программной системы

За основу при разработке данной программной системы взята логика построения программы имитации одноканальной СМО M / M /1 [1]. При этом кардинально переработана как сама программа, так и вся ее логика с целью имитации произвольных входных потоков и произвольного закона времени обслуживания. Кроме того, система имеет равнодоступные каналы с возможными ограничениями на длину очереди. Вместо пуассоновского входного потока и экспоненциального закона времени обслуживания разрабо-

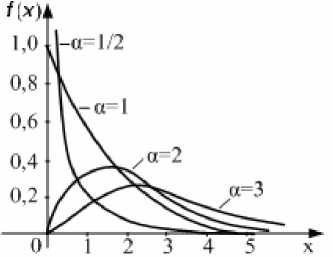
Рис. 1. Графики функции плотности гамма-распределения танная программа генерирует входной поток и времена обслуживания по гамма-распределению. Как известно, в зависимости от параметров распределения α и β , коэффициент вариации гамма-распределения может быть как больше, так и меньше либо равен 1. Поэтому данный закон распределения является достаточно широким. Плотность гамма-распределения описывается функцией

f (^x) = <

р - ^а x

α -1 - x / β e

0,

Г (а)

x > 0;

x < 0,

с числовыми характеристиками М ( Х ) = α·β; D ( Х ) = α β². Путем варьирования параметров α и β можно получать произвольные распределения на уровне их двух первых моментов. На рис. 1 приведены графики функции плотности в зависимости от ее параметров.

очередью длина очереди взята максимально возможной, чтобы избежать ее переполнения. Если в очереди еще есть место, время поступления требования помещается в конце очереди.

Схемы алгоритмов поступления и ухода требований изображены на рис. 2 и рис. 3, соответственно. Если устройство свободно на момент поступления требования, то задержка требования в очереди будет равна 0, что, тем не менее, считается задержкой, и число задержек требований увеличивается на 1. Устройство переводится в состояние занятости, а в списке событий планируется время ухода по окончании обслуживания поступившего требования.

Если после ухода требования очередь остается пустой, устройство переходит в состояние незанятости, а учет ухода требований отменяется, поскольку следующим событием должно быть поступление.

Саму программу удобно собирать из блоков нескольких подпрограмм. Это помогает сделать более понятной ее логику и взаимодействие компонентов. Кроме основной программы, программа моделирования включает подпрограммы для инициализации, синхронизации, генерирования отчетов и случайных величин, имеющих гамма-распределение.

В первую очередь генерируется время очередного поступления заявки в систему и помещается в список событий. Все списки событий создаются согласно схемам алгоритмов поступления и ухода требований, приведенным ниже на рис. 2-3. Затем проверяется занятость устройства. Когда устройство занято, число требований в очереди увеличивается на 1, и мы проверяем, заполнена ли память, выделенная для хранения очереди. Если очередь уже заполнена, генерируется сообщение об отказе на обслуживание, и текущее требование теряется. В случае СМО с бесконечной

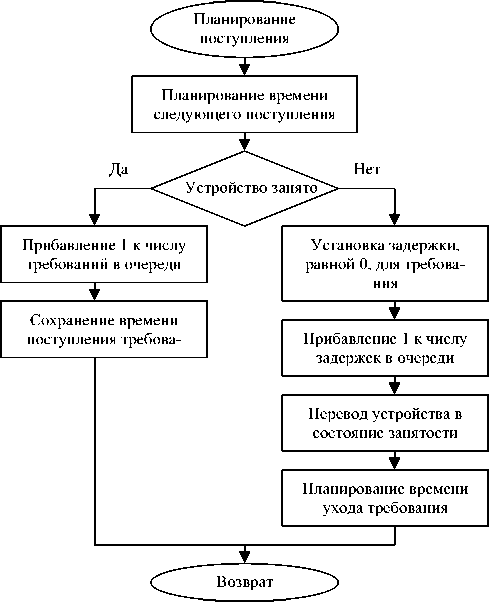
Рис. 2. Схема алгоритма поступления требования в СМО

Если же после ухода в очереди остается еще одно или несколько требований, первое в очереди требование оставляет очередь и переходит на обслуживание. При этом длина очереди уменьшается на 1, а продолжительность задержки этого требования вычисляется и регистрируется соответствующим статистическим счетчиком. Число задержек в очереди увеличивается на 1, и плани- руется время ухода требования, перешедшего на обслуживание. После этого оставшиеся в очереди требования (если таковые имеются) передвигаются на одно место вперед.

Событие ухода

Очередь свободна

Вычитание 1 из числа требований в очереди

Перевод устройства в состояние незанятости

Удаление события ухода с рассмотрения

Вычисление продолжительности задержки и сбор статистики

Прибавление 1 к числу задержек в очереди

Планирование времени ухода для требования

Перемещение каждого требования в очереди на одно место вперед

Рис. 3. Схема алгоритма ухода требования в СМО с бесконечной очередью

Когда очередь имеет конечную длину, то есть в случае СМО с потерями, при поступлении требования на обслуживание добавляется проверка на переполнение очереди. Если очередь уже заполнена, требование отклоняется и фиксируется время его отклонения, после чего планируется время следующего события. Число отклоненных требований увеличивается на 1. При этом схема поступления требований изменится так, как показано на рис. 4.

Входными данными для моделирования являются значения загрузки ρ и коэффициентов вариаций входного потока сλ и времени обслуживания сμ . Для проведения экспериментов в целях верификации программы эти параметры варьировались в широком диапазоне: ρ = [0,1; 0,3; 0,5; 0,7; 0,9], сх = сц = [0,1; 0,5; 1; 2; 5]. При этом для уменьшения числа варьируемых параметров время обслуживания положено равным 1 (нормированное время обслуживания), то есть μ = 1. Для генерации случайных интервалов времени для входного потока и времени обслуживания используем генератор гамма-распределения, алгоритм которого описан ниже. Для этого параметры этого распределения надо согласовать с входными параметрами потоков р, с^, Сц.

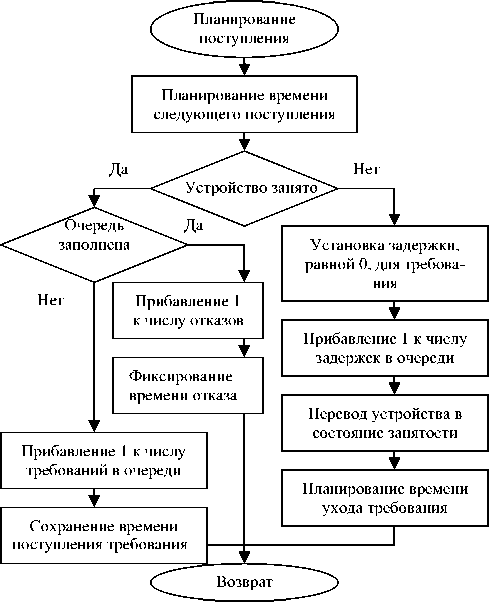
Рис. 4. Схема алгоритма поступления требования в СМО с конечной очередью с потерями

С учетом равенств (1) для данной модели полу-αоβо чим ρ =      , где αо и βо

αпβп распределения для случайного времени обслуживания, α п , β п – параметры гамма-распределения для случайного времени поступления. С учетом 2

того, что а = 1 / c ,где с -коэффициентвариации, μ = 1 и ρ = [0,1;0,3;0,5;0,7;0,9], получим значения параметров α и β гамма-распределения, то есть распределения времен поступления и обслуживания требований: а о = ап = [100;4;1;0,25;0,04], для распределения времени поступления р п = 1/(а п X п), для распределения времени обслуживания βO = 1 / αO.

Таким образом, все входные параметры для моделирования определены. Сам процесс моделирования начинается с вызова основной программы инициализации. В начальный момент времени обслуживающие приборы свободны (переменные состояния модели установлены в исходную позицию 0). Для значений времени поступления и обслуживания генерируются случайные значения и помещаются в отдельные одномерные массивы (изначально они пустые).

После завершения инициализации управление передается основной программе, которая вызывает синхронизирующую программу для определения первоочередного события из списка.

Для начала это будет программа поступления, которая выполнит обработку поступления первого требования и определит время поступления очередного требования. При этом изменяются состояние системы со свободного на занятый, статистические счетчики и модельное время. Затем управление передается программе ухода требования и выполняются аналогичные действия.

Алгоритм работы генератора гамма-распределения

Таким образом, случайные времена поступления требований и их обслуживания имеют гамма-распределение. Теперь перейдем к алгоритму работы генератора гамма-распределения [1]. За-метим,чтопрификсированном X ~ gamma(a,P) для любого в > 0 можно получить X' = P X , так что достаточно воспользоваться следующим алгоритмом для моделирования величин из распределения gamma (a,1) [1]. Сначала рассмотрим случай, когда параметр 0 < α < 1. Заранее определим b = (e + a) / e .

• 1.    Генерируем U 1 ~ U (0,1), где U означает равномерный закон и пусть P = bU ₁ . Если P > 1 , переходим к шагу 3. В противном случае переходим к шагу 2.

• 2.    Допускаем Y = P ¹ / ^a, , генерируем U 2 ~ U (0,1). Если U 2 < e ^{- Y} , возвращаем X = Y . В противном случае возвращаемся к шагу 1.

• 3.    Допускаем Y = - ln[(b - P)/ a] ,генерируем U 2 ~ U (0,1). Если U 2 <  Y ^{a 1} , возвращаем X = Y . В противном случае возвращаемся к шагу 1.

Для случая α > 1 сначала определим константы a = V2a -1 , b = a - In 4, q = a + 1/ a , 6 = 4,5 , d = 1 + ln0 . Далее

• 1.    Генерируем U ₁ и U ₂ как независимые и одинаково распределенные случайные величины с распределением U (0,1).

• 2.    Допускаем V = a ln[U 1 /(1 - U 1 )], Y = ae V Z = U 12 U 2 и W = b + qV - Y .

• 3.    Если W + d - 0Z >  0 , возвращаем X = Y .

• 4.    Если W ≥ ln Z , возвращаем X = Y . В противном случае переходим к шагу 1.

В противном случае переходим к шагу 4.

Здесь шаг 3 – это добавленная предварительная проверка, в случае прохождения которой можно избежать вычисления логарифма на шаге 4 [1].

Для случая α = 1 моделируем экспоненциальное распределение.

РезультатыэкспериментовдляСМО с бесконечной очередью

Верификация программной системы проводилась путем сравнения основных характеристик СМО с известными результатами теории массового обслуживания, а также с результатами двумерной диффузионной аппроксимации процессов функционирования СМО [2-3]. В таблице 1 приведены результаты работы программы по среднему количеству требований в СМО с бесконечной очередью в зависимости от загрузки ρ (рассмотрены случаи малой, средней и большой загруз-

Таблица 1. Среднее количество требований в СМО с бесконечной очередью в зависимости от загрузки, коэффициентов вариации входного потока и потока обслуживания

ρ	с λ     с μ	0,1	0,5	1	2	5
0,1	0,1	0,100\0,100	0,101\0,101	0,105\0,105	0,114\0,117	0,198\0,211
	0,5	0,111\0,111	0,111\0,111	0,131\0,115	0,140\0,117	0,205\0,220
	1	0,111\0,111	0,111\0,112	0,112\0,115	0,147\0,125	0,231\0,232
	2	0,115\0,118	0,122\0,122	0,134\0,133	0,160\0,171	0,368\0,360
	5	0,416\0,421	0,471\0,394	0,601\0,431	0,608\0,586	1,092\1,076
0,5	0,1	0,501\0,506	0,529\0,534	0,591\0,671	1,284\1,344	6,403\6,429
	0,5	0,531\0,534	0,576\0,576	0,737\0,737	1,459\1,446	6,598\6,607
	1	0,560\0,670	0,791\0,741	0,991\0,945	1,719\1,714	7,125\6,934
	2	1,704\1,748	0,713\1,704	1,569\1,911	2,121\2,764	9,627\8,145
	5	9,879\11,449	10,606\11,421	11,205\11,633	13,337\12,535	18,999\17,945
0,9	0,1	0,903\0,964	1,964\1,913	4,848\4,848	13,127\16,798	103,896\100,819
	0,5	2,045\1,996	2,745\2,925	6,659\5,886	22,713\17,831	104,146\102,213
	1	5,132\5,145	7,548\6,110	9,013\9,096	27,762\21,062	107,890\105,380
	2	17,64\18,135	19,958\19,036	20,983\22,112	39,097\34,153	111,876\118,207
	5	111,04\111,13	112,92\112,00	114,09\115,12	125,36\127,55	214,09\212,60

Таблица 2. Среднее значение между заявками в выходном потоке в зависимости от загрузки и коэффициента вариации времени обслуживании для СМО M/G/1

ρ	с с λ      μ	0,1	0,5	1	2	5
0,1	1	10,101	10,101	10,101	10,101	10,101
0,5	1	2,013	2,013	2,013	2,013	2,013
0,9	1	1,119	1,119	1,119	1,119	1,119

Таблица 3. Дисперсия выходного потока в зависимости от загрузки и коэффициента вариации потока обслуживания для СМО M/G/1

ρ	с λ      с μ	0,1	0,5	1	2	5
0,1	1	100,068	101,075	103,075	103,075	104,003
0,5	1	3,861	4,053	4,054	4,013	4,070
0,9	1	1,236	1,236	1,239	1,242	1,257

Таблица 4. Вероятность потери P _отк и среднего времени задержки W в зависимости от длины очереди

m 0,1 1 2 2 о,1 0,0004/0,112 0,003/0,149 0,0035/0,255 0,5 0,0306/0,452 0,0677/0,803 0,0983/2,557 0,9 0,0917/2,086 0,1366/3,710 0,1906/7,371 5 0,1 0,0000/0,112 0,0000/0,149 0,0000/0,255 0,5 0,0004/0,343 0,0011/0,888 0,0073/2,356 0,9 0,0017/3,381 0,0064/6,502 0,0337/17,542 10 0,1 0,0000/0,112 0,0000/0,149 0,0000/0,252 0,5 0,0002/0,401 0,0002/0,890 0,0006/2,411 0,9 0,0016/4,176 0,0062/8,122 0,0096/20,606 ки) и коэффициентов вариации входного потока сλ и времени обслуживания сμ . В таблицах 2 и 3 приведены значения среднего и дисперсии времени выходного потока в зависимости от тех же параметров. В таблице 1 через дробь указаны результаты, полученные в результате двумерного диффузионного приближения СМО [2-3].

Анализ полученных результатов сравнением с известными результатами для систем M / M / 1 и M / G / 1 показывает, что они хорошо согласуются. Относительную погрешность в 5-6% вполне можно отнести к статистической погрешности имитационного моделирования.

РезультатыэкспериментовдляСМОс конечной очередью и потерями

В качестве результатов программы для СМО с конечной очередью приведены значения вероятности потери требований P _отк в зависимости от размера буфера m , загрузки ρ и коэффициента вариации времени обслуживания с _μ и среднее время ожидания W в зависимости от тех же па-

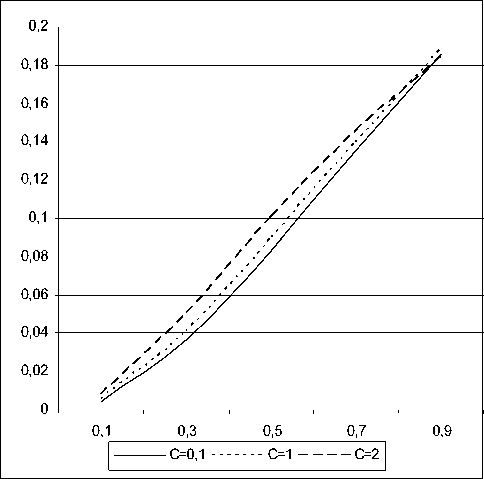
Рис. 5. Зависимость вероятности потери Pотк от загрузки ρ для различных значений сμ для m = 2

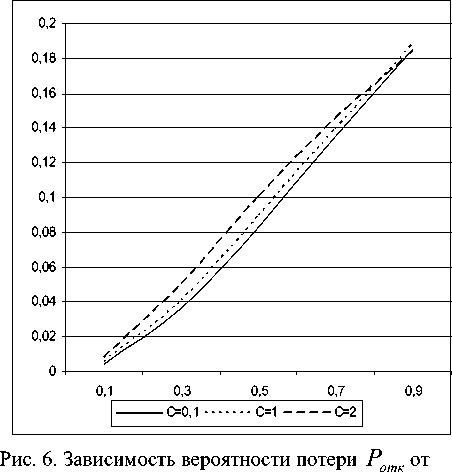
загрузки ρ для различных значений с _μ для m = 10

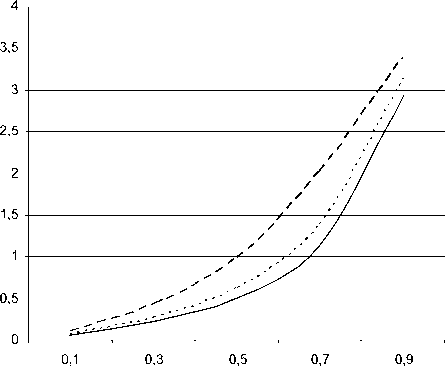
С=0,1        С=1        С=2

Рис. 7. Зависимость среднего времени ожидания

W от загрузки ρ для различных значений с _μ для m=10.

раметров для СМО M / G / m , для которой эти результаты известны. В таблице 4 указаны значения P _отк и через дробь значения W .

Сравнение полученных в этом разделе результатов, с результатами формулы потерь Эрланга, также доказывает адекватность полученной модели.

Заключение

• 1.    Теоретически обоснованы алгоритмы функционирования многоканальной СМО с бесконечной очередью и с конечной очередью с возможными потерями требований.

• 2.    На основе данных алгоритмов разработана программная система расчета характеристик таких СМО. Программная система реализована на универсальном языке C ++ по переключательной схеме: «0», если СМО с бесконечной очередью; «1», если СМО с конечной очередью и с потерями. В первом случае входными параметрами являются: количество каналов системы;интенсивность и коэффициент вариации входного потока; интенсивность и коэффициент вариации времени обслуживания. Во втором случае входными параметрами, кроме вышеперечисленных, являются также размеры буферов каналов.

• 3.    Проведенные эксперименты на программной системе для широкого диапазона

• 4.    Разработанные алгоритмы и программная система могут быть использованы в качестве математической модели функционирования активного оборудования компьютерных и телекоммуникационных сетей при широком диапазоне изменения параметров трафика.

Выходными параметрами в обоих случаях являются основные характеристики СМО.

изменения параметров потоков и полученные при этом результаты подтверждают правильность логики построения программы, а также адекватность разработанной имитационной модели массового обслуживания.