Программное обеспечение для анализа волновых движений в моментных средах на многопроцессорных вычислительных системах

Моментная теория упругости Коссера [1; 2] служит для описания деформации материалов с микроструктурой: композитов, гранулированных, порошкообразных, микроразрушенных и микрополярных сред. В отличие от обычной теории упругости в ней неявно присутствует малый параметр среды – характерный размер частиц микроструктуры, поэтому при численном решении задач расчеты необходимо выполнять на сетках, размер ячеек которых меньше этого параметра. При решении динамических задач в пространственной постановке эффективными оказываются параллельные алгоритмы, поскольку они позволяют распределять вычислительную нагрузку между большим числом узлов кластера, что дает возможность существенно измельчать расчетные сетки, повышая тем самым точность численного решения.

Математическая модель. В модели моментной среды, кроме поступательного движения, которое характеризуется вектором скорости v , рассматриваются независимые повороты частиц с вектором угловой скорости щ, и наряду с тензором напряжений у, компоненты которого несимметричны, вводится несимметричный тензор моментных напряжений m . Полную систему уравнений модели образуют уравнения движения, кинематические соотношения и обобщенный закон линейной теории упругости:

Λ ^&= ∇ v + ω, M ^&= ∇ ω,             (1)

σ=λ(δ:Λ)δ+2μΛs+2αΛa, m=β(δ:M)δ+2γMs+2εMa, где р - плотность среды; g - вектор массовых сил; q - вектор моментов; Л и M- равные нулю в естественном (ненапряженном) состоянии среды тензоры деформаций и кривизны; j – инерционный параметр, равный произведению момента инерции частицы относительно оси, проходящей через ее центр тяжести, на число частиц в единице объема; 5 - символ Кронекера; X, ц, a, Р, у и £ -коэффициенты упругости для изотропного материала. В (1) также используются общепринятые обозначения и операции тензорного анализа: двоеточие означает двойную свертку, точка над символом – производную по времени, звездочка – транспонирование, верхними индексами s и a отмечены симметричная и антисимметричная составляющие тензоров. С антисимметричной составляющей, где это необходимо, отождествляется соответствующий ей вектор, в частности в уравнения вращательного движения входит вектор тензора о a = (о - о ) / 2 . Для оценки линейного параметра микроструктуры материала справедлива формула r=5j(2ρ) , основанная на модельном представлении о среде как о плотной упаковке ансамбля шарообразных частиц одинакового радиуса.

В пространственном случае система уравнений (1) включает 24 уравнения относительно 24 неизвестных функций. Можно переписать ее в матричной форме [3]:

AU = B^X U ,1 + B ² U , ₂ + B ³ U ,3 + QU + G , (2) где U – вектор-функция, составленная из компонент векторов скорости и угловой скорости, несимметричных тензоров напряжений и моментных напряжений. В декартовой системе координат U принимает вид

U =( v ₁, v ₂, v ₃, σ₁₁, σ₂₂,

σ33, σ23, σ32, σ31, σ13, σ12, σ21,

ω₁, ω₂, ω₃, m ₁₁, m ₂₂, m ₃₃, m ₂₃, m ₃₂, m ₃₁, m ₁₃, m ₁₂, m ₂₁).

В вектор G входят массовые силы и моменты. Матрицы-коэффициенты A , B ¹, B ² и B ³ симметричны, а матрица Q антисимметрична. Матрица A положительно определена, если выполняются условия, ограничивающие допустимые значения параметров среды:

3Z + 2ц, ц, а > 0, 3в + 2y, y, £ > 0.

При выполнении этих условий потенциальная энергия упругой деформации представляет собой положительную квадратичную форму, а система уравнений (2) является гиперболической по Фридрихсу.

Для гиперболической системы корректно поставлена краевая задача с начальными данными и диссипативными граничными условиями [4; 5], выполнение которых для любых двух векторов-функций U и Û в точках границы обеспечивает выполнение неравенства

( U - U ) ( n 1 B 1 + n ₂ B ² + n ₃ B ³ ) ( U - U ) < 0.

К диссипативным, в частности, относятся условия в напряжениях, которые формулируются в рамках модели моментной среды следующим образом:

• ^о ik n i = P k , m ik n i = q k,

где n – вектор внешней нормали; p и q – заданные на границе векторы внешних усилий и моментов (сумми- рование производится по повторяющимся индексам), а также условия в скоростях: v = vq, ю = ю0.

Вычислительная технология. Для проведения численного исследования краевых задач для системы (2) разработан параллельный вычислительный алгоритм, основанный на методе двуциклического расщепления по пространственным переменным [3]. Полученные в результате этого расщепления одномерные системы решаются с помощью явной монотонной ENO-схемы с предельной реконструкцией решения.

Алгоритм реализован в виде комплекса программ на языке Fortran-90 с использованием библиотеки MPI ( Message Passing Interface ) по технологии SPMD ( Single Program – Multiple Data ). Распараллеливание выполнено на основе блочного разбиения области решения задачи. Программный комплекс позволяет проводить расчеты распространения волн, вызванных внешними механическими воздействиями, в массиве среды, составленном из произвольного числа разнородных блоков с криволинейными границами. Внутренние границы раздела блоков считаются согласованными, что в общем случае достигается с помощью фиктивного разбиения расчетной области. На внешних границах допускается постановка основных типов краевых условий в напряжениях и скоростях, а также неотражающих условий, моделирующих беспрепятственное прохождение волн. Универсальность программ обеспечивается за счет специальной упаковки переменных, используемых на каждом из вычислительных узлов кластера, в одномерные массивы большой размерности.

Необходимые для расчета исходные данные должны представляться в виде текстовых файлов, организованных по типу реляционных таблиц. Один из таких файлов содержит механические параметры материалов в блоках, другой – условия нагружения, в третьем хранится информация о блочной структуре массива: количество слоев по переменной x ₁, количество полос в слое по переменной x ₂ и количество блоков в полосе по переменной x ₃, координаты вершин блоков, а также идентификационные номера материалов и пространственные размерности сеток. Расчетные сетки, вообще говоря, не стыкующиеся на межблочных границах, в простейшем варианте строятся с помощью кубических эрмитовых сплайнов. Склейка решений на границах раздела выполняется специальной процедурой, в которой решение на измельченной сетке, получаемой пересечением граничных ячеек соседних блоков, находится с помощью уравнений на характеристиках, а затем переносится на исходные сетки методом осреднения.

Каждый из узлов кластера при выполнении программы-препроцессора упаковывает исходные данные в двоичный файл прямого доступа – файл вещественных чисел, в который поблочно записываются параметры материала, часть сетки, приходящаяся на этот узел, и начальные значения решения, и файл целых чисел, содержащий соответствующие им адреса (указатели) – порядковые номера первых элементов. Вещественные файлы такой же структуры в дальнейшем будут создаваться основной программой для организации контрольных точек при счете и для последующего анализа полученных результатов. Суммарный размер таких файлов может значитель- но превышать объем оперативной памяти отдельного процессора.

Каждый процессор при старте основной программы считывает целочисленный файл и соответствующий ему вещественный файл. Далее целочисленный массив (образ целочисленного файла) редуцируется, т. е. параметры сетки и указатели принимают в нем индивидуальные значения для данного узла. Распределение расчетной области между процессорами производится по принципу равномерной загрузки: если размерность сетки какого-либо блока больше средней размерности в расчете на один узел кластера, то этот блок обслуживается несколькими узлами, и наоборот, один и тот же узел обслуживает несколько блоков, если их суммарная размерность не превосходит среднюю размерность.

Для примера рассмотрим расчетную область в виде куба для двухслойной разнородной среды (слои разделены между собой поверхностью типа гиперболического параболоида), разбитую на 8 криволинейных блоков, с грубой разностной сеткой, построенной в каждом из блоков автономно (рис. 1, а ), а также выделенную четверть расчетной области (два блока) (рис. 1, б ) с учетом симметрии задачи, равномерно распределенной программой-препроцессором между 72 процессорами: 4³ = 64 процессора обслуживают верхний блок и 2³= 8 – нижний.

Основная программа на каждом узле кластера выполняется одни и те же вычисления, которые сводятся к взаимно согласованной поэтапной реализации метода расщепления по пространственным переменным на каждом шаге по времени. Исключение составляют процессоры, производящие помимо этого еще и склейку решений на внутренних границах. Условия склейки реализуются по следующей схеме. Процессоры, обслуживающие приграничные блоки (блоки, расположенные по обе стороны от границы раздела), передают необходимую информацию одному из процессоров, который производит расчет всей границы в целом и рассылает результаты в обратном направлении. Из соображений минимизации количества пересылок используются различные варианты разбиений расчетной области: 1D, 2D или 3D. Если разделяющая блоки граница лежит внутри области, обслуживаемой одним процессором, то такая склейка выполняется автономно.

При решении одномерных систем уравнений в блоке используется обычная технология законтурных ячеек (рис. 2): каждый процессор сначала обменивается с соседними процессорами граничными значениями своих данных, а затем пересчитывает искомые величины в соответствии с разностной схемой и с учетом данных, полученных от соседних процессов. Обмен данными осуществляется с помощью функции Sendrecv библиотеки MPI. Для минимизации времени счета объем блока передаваемых данных (и, следовательно, число передач) варьируется путем совместного решения определенного количества одномерных систем.

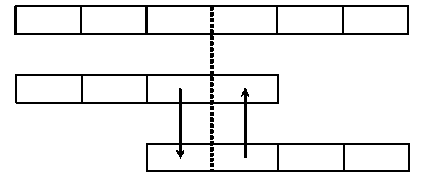
Рис. 2. Схема обмена между процессорами с законтурными ячейками

Процедуру сжатия файлов, содержащих результаты счета, выполняет программа-постпроцессор, поскольку размер таких файлов может быть очень большим и для их транспортировки по сети потребуются значительные ресурсы. Графический вывод результатов осуществляется с помощью специальных программ, предназначенных для обычного персонального компьютера.

Алгоритм сжатия файлов. Идея сжатия файлов числовых данных для компактного хранения и передачи решения заимствована в методе разделения переменных, в соответствии с которым заданная скалярная функция u , зависящая от вектора x = ( x ₁, x ₂, ..., x_n ), разлагается в бесконечный ряд. Элементы этого ряда представляют собой произведения одномерных функций:

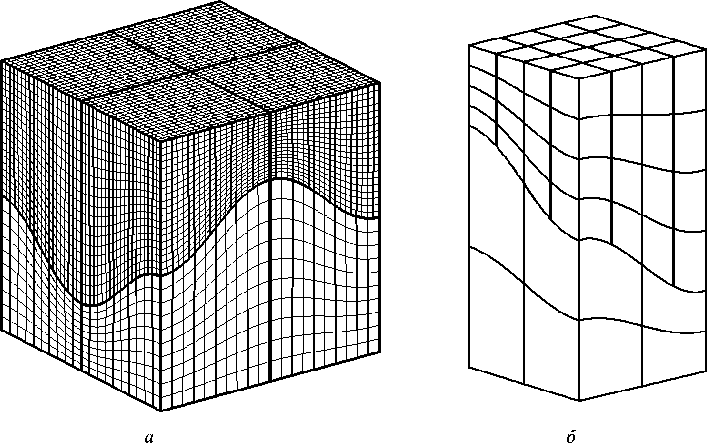
Рис. 1. Сетка и четверть расчетной области с разбиением на процессы

го u (%) = 2 X k Xk 4 (X) Xk ,2( x 2) K Xk ’ n (Xn ) .

k = 1

Дискретный аналог ряда с разделенными переменными выглядит следующим образом:

и = У X, X k ,1 X k > ² X k , n .        и)

i 1 i 2 k i n    i—i ^k 1     i 2         i n               ⁽⁾

k = 1

Обычно в методе разделения переменных базисные фун- khuh X⁶² , ..., X k-n являются собственными функциями некоторого дифференциального оператора. В данном случае они определяются из соображений наилучшего приближения и . При вычислении первого слагаемого ряда решается задача условной минимизации квадратичной функции

M1 M 2

2 2 к 2 (u,.2Ki„ -XX;Xi2 кXn )2(4)

4 = 1 i 2 =1 in =12

относительно переменных X, X 1 , ^X i 2 , • K, X in • При этом предполагается, что выполнены следующие условия нормировки:

M1    . , M 2, ,

2 (X*)2 = 2 (X2)2 = i'1 = 1               i 2 = 1

M n

= к = 2 ( X- )² = 1.

in in = 1

Точка минимума (4) удовлетворяет системе уравнений, которая может быть получена с учетом условий нормировки методом множителей Лагранжа:

M 1 M 2   M n

X =у УкУ и,, , X ¹ X ² к Xⁿ Z—iZ—1 Z—i i 1 i 2 ^K i n i 1 i 2 i n i '1 = 1 i 2 = 1 i n = 1

X k = i_k

M1 Mk-1 Mk+1   Mn у к У  у к у и    X1 к Xk-1 Xk+1.

^     ^    Z-^     Z-i  i 1 1 2 ^к in i 1       Ik - 1 Ik + 1

i 1 = 1     i k - 1 = 1 i k + 1 = 1     i n = 1

.

M k

^M 1    M k - 1 M k + 1    M

"" k — 1 X^ + 1 i k - 1    i k + 1

мом вычисления наибольшего собственного значения и соответствующего собственного вектора симметричной неотрицательно определенной матрицы, полученной степенным методом Люстерника.

Описанный выше алгоритм сжатия и вопросы сходимости итерационного процесса и ряда (3) с разделенны- ми переменными в двумерном случае детально исследованы в [6-8], где показано, что скорость сходимости ряда (3) определяется гладкостью аппроксимируемой функции и. Однако для n независимых переменных эти вопро- сы еще далеки от своего полного решения.

В качестве примера, иллюстрирующего работоспособность алгоритма сжатия, на рис. 3 приведено графическое изображение исходного файла данных, моделирующего сферическую ударную волну на с етке из 50 x 50 x 50 ячеек (слева), и результата сжатия (справа). Были вычислены 7 членов ряда. Коэффициент сжатия файла -1/120. Относительная погрешность, характеризующая потерянную информацию, равна 1,5 %.

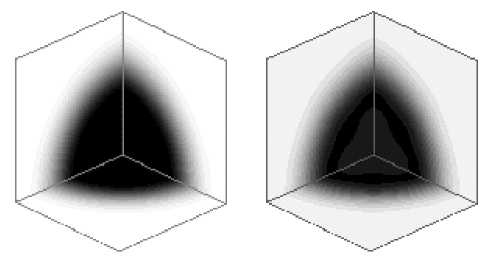
Рис. 3. Сферическая ударная волна и результат сжатия

Также приведем исходную картину и результат сжатия файла для функции

и ( X 1 , X 2 , X з ) =

_ ^{- k (} r ^- r 0 ^{) 2 /} r ²    2_ 2    2    2.

• — e            ( r — X 1 + x 2 + x з ),

описывающей локализацию решения на сфере радиуса r ₀ (рис. 4). Здесь безразмерный параметр локализации k = 20, а радиус сферы равен наибольшей диагонали параллелепипеда. В данном случае число членов ряда равно 12, относительная погрешность вычислений - 2,2 %, коэффициент сжатия - 1/70. Число членов ряда, необходимое для достижения заданной погрешности, растет с увеличением степени локализации, т. е. коэффициента k . Таким образом, рассматриваемый алгоритм сжатия при наличии локализаций решения в весьма узких областях становится малоэффективным.

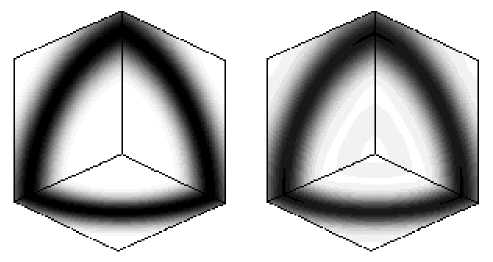
Рис. 4. Локализация решения на сфере и результат сжатия

Проведенная серия расчетов показала, что итерационный процесс на основе формул (5) и (6) является экономичным в том смысле, что требуемое для заданной точности число итераций метода последовательных приближений практически не зависит от размерности дискретной задачи.