Программное обеспечение компьютерного сепаратора для очистки зерна

Компьютерный сепаратор предназначен для очистки и сортировки зерновых культур, таких как пшеница, овес, ячмень и рожь, а также может быть использован для очистки других зернобобовых и масличных культур (рис. 1). Послеуборочная очистка и сортировка зерна являются одними из важных операций в производстве зерна, а имеющаяся в сельскохозяйственном производстве зерноочистительная техника морально устарела. Назрела необходимость разработки принципиально нового оборудования, основанного на новых технологиях. Компьютерный сепаратор способен в реальном режиме времени определять геометрические параметры любого зерна, цвет и наличие дефектов в зерне. При определении геометрических параметров зерна определяются длина, ширина, толщина и форма контура зерна. Для анализа формы поверхности зерна в системе заложена возможность восстановления видимой части поверхности зерна. На основании полученных данных производить удаление тех зерен, которые не соответствуют предъявляемым критериям. Удаление зерна производится с помощью вакуумного отсоса в специальную емкость. Сепаратор позволяет подсчитать количество зерен, их средние геометрические размеры и вести статистическую обработку данных. Компьютерный сепаратор также может быть использован на семенных станциях, где требуется небольшая производительность.

Аппаратная часть компьютерного сепаратора

В аппаратную часть компьютерного сепаратора (рис. 2) входят ленточный транспортер с приводом 3, система сортировки зерна 7, система технического зрения (СТЗ) 4, система подачи и приема зерна 1 и компьютер. Ленточный транспортер с приводом позволяет перемещать зерна по транспортерной ленте с разной скоростью в зависимости от количества зерна, находящегося на нем. Изменение скорости перемещения ленты обусловлено быстродействием сортировки зерна системы и СТЗ. Транспортерная лента должна быть черного цвета, что позволит легко выделить на нем зерна, т.е. произвести сегментацию на цифровом изображении. Система сортировки зерна (рис 3) состоит из рамы сортировочного узла с двумя направляющими, по которой перпендикулярно транспортерной ленте перемещается каретка со всасывающей головкой. Для перемещения каретки и точного позиционирования всасывающей головки применяется шаговый двигатель с блоком управления. Всасывающая головка системы сортировки связана через гибкий шланг с вакуумным электроклапаном, который срабатывает, когда необходимо удалить из транспортерной ленты посторонние примеси или зерна, не удовлетворяющие предъявляемым требованиям, в специальный накопитель. Система технического зрения предназначена для получения оцифрованного видеопотока. Из видеопотока можно выделить отдельные цифровые изображения, по которым определяются геометрические параметры каждого зерна (длина, ширина, толщина и форма контура зерна), цвет и наличие дефектов в зерне. В систему технического зрения входят две видеокамеры, лампа для освещения сцены на транспортерной ленте и плата оцифровки в случае применения аналоговой видеокамеры. Современные цифровые камеры позволяют передавать видеосигнал на прямую без платы оцифровки через стандартный интерфейс компьютера IEEE1394 (FireWire, i-Link) или USB2. Из двух видеокамер первая устанавливается над транспортерной лентой так, чтобы оптическая ось объектива видеокамеры была бы перпендикулярна плоскости транспортерной ленты. С помощью этой камеры определяются длина, ширина и форма контура каждого зерна. Вторая видеокамера устанавливается под углом к плоскости транспортерной ленты для определения толщины зерна. Система подачи подает зерно из бункера на транспортерную ленту. При этом подача должна производиться таким образом, чтобы зерна на транспортерной ленте размещались в один слой, это связано с тем, что при выделении границ зерна на цифровом изображении не должно быть наложения одного зерна на другое, так как это может привести к неправильному определению геометрических характеристик зерна. Отсортированное зерно по транспортерной ленте попадает в приемный бункер.

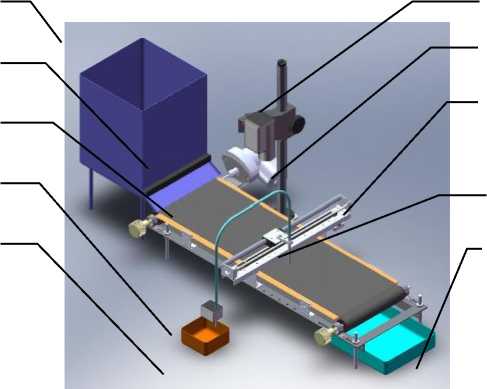
Рис.2. Устройство компьютерного сепаратора

Рис.3. Система сортировки зерна

Устройство компьютерного сепаратора

Компьютерный сепаратор состоит из аппаратной части и программного обеспечения.

Программное обеспечение компьютерного сепаратора

Программное обеспечение состоит из следующих разделов: модуль захвата цифровых изображений из видеопотока, калибровка системы технического зрения, предварительная обработка, определение порога бинаризации и бинаризация, сегментация, определение границ зерен, определение геометрических параметров зерен, определение цвета зерна и наличия дефектов зерна, управление системой сортировки зерна – удаление дефектных зерен и примесей, определение количества зерен и средних значений геометрических размеров зерен, статистическая обработка данных.

Захват цифровых изображений из видеопотока

Изображение зерен на транспортерной ленте в оцифрованном виде передается с видеокамер на компьютер через интерфейс компьютера FireWire (IEEE1394). Для получения отдельных цифровых изображений с видеопотока используется библиотека Microsoft Video for Windows SDK (AVICAP32.DLL), которая позволяет открыть видеоустройство для захвата видео, сохранять отдельные кадры с устройства, как файлы в формате *BMP на диск, а также записывать видеопоток в файл *.AVI (со звуком, но без предварительного просмотра).

Калибровка системы технического зрения

Точность определения геометрических параметров зерна зависит от калибровки системы технического зрения. При калибровке СТЗ необходимо решить две задачи - определение внешних и внутренних параметров видеокамер.

Определение внешних параметров камеры сводится к определению положения камеры в системе координат предметного пространства и углов поворота камеры в этой системе. При установлении внутренних параметров видеокамеры решаются следующие задачи: определение точки пересечения оптической оси с плоскостью изображения, определение расстояния от оптического центра объектива до плоскости изображения, определение коэффициентов перевода между единицами измерения на плоскости изображения и в предметном пространстве, а также решение задачи уменьшения искажений, внесенных оптической системой камеры. В предложенной нами методике калибровки камеры используется математический аппарат проективной геометрии, определение параметров камеры осуществляется с помощью правильного шестиугольника, расположенного на плоскости транспортера. Углы поворота системы координат камеры относительно системы координат предметного пространства обозначим следующим образом - угол тангажа - ψ , курса - χ (рысканья) и крена - ϕ (рис. 4). Предметная ортогональная система координат будет задана осями x,y,z, а ортогональная система координат изображения будет задана осями u,v,e. Шестиугольник P 1 ,P 2 ,P 3 ,P 4 ,P 5 ,P 6 пусть располагается в координатной плоскости Λ , инцидентной осям координат x и y, которую будем называть предметной плоскостью. Пусть сторона (P 1 P 2 ) параллельна оси 0x. Изображение шестиугольника P 1 ',P 2 ',P 3 ',P 4 ',P 5 ',P 6 ' располагается в картинной плоскости Π . Центр проецирования (оптический центр объектива) пусть располагается в точке S, а ось объектива пусть совпадает с осью e системы координат изображения. Две другие оси u и v системы координат изображения расположены в картинной плоскости Π и направлены параллельно границам кадра p и g соответственно. Точкой N' обозначим основание перпендикуляра, опущенного из точки S на картинную плоскость Π . Точка N' является началом системы координат изображения камеры и, одновременно, точкой пересечения оптической оси объектива с плоскостью изображения камеры. Расстояние между точками S и N' является расстоянием от центра проецирования S до картинной плоскости, обозначим его через d. Причем, надо заметить, картинная плоскость Π на рисунке 4 показана расположенной между центром проецирования S и предметной плоскостью Λ , хотя реально она не располагается перед центром проецирования. Буквой m обозначим коэффициент преобразования между единицами измерения на изображении и предметной системы координат. Точкой N обозначим точку пересечения оси e с предметной плоскостью. Расстояние между точками N' и N обозначим через l .

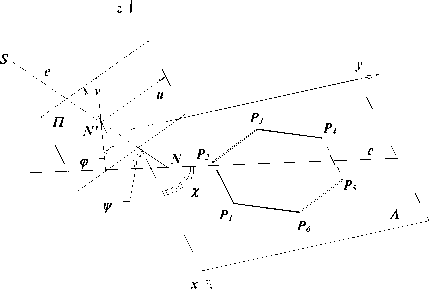
Рис. 4. Углы поворота системы координат камеры относительно системы координат предметного пространства

Определение точки пересечения оптической оси объектива камеры с плоскостью изображения

В процессе калибровки камеры необходимо знать положение точки пересечения оптической оси объектива камеры с плоскостью изображения N'. При решении этой задачи нами предлагается использовать возможность изменения фокусного расстояния объектива камеры. Для реализации этого метода плоский объект прямоугольной формы, окрашенный в белый цвет, закрепляется на черном планшете.

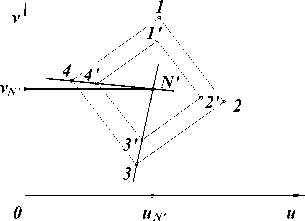
Рис. 5 Определение точки пересечения оптической оси объектива камеры с плоскостью изображения

Планшет ориентируется таким образом, чтобы оптическая ось камеры была бы перпендикулярной по отношению к планшету. Необходимо сфотографировать этот объект при различных значениях фокусного расстояния. По полученным снимкам производится выделение контура этого объекта на цифровых изображениях (рис. 5) и определяются угловые точки на объекте (1,2,3 и 4). Если построить прямые, проходящие через соответствующие угловые точки, то эти прямые пересекутся в одной точке N'. Эта точка и будет точкой пересечения оптической оси объектива камеры с плоскостью изображения, и координаты этой точки должны быть неизменными при любых значениях фокусного расстояния объектива камеры.

Проведя серии экспериментов, можно достаточно точно рассчитать координаты точки N' (u _N ' ,v_N) в системе координат изображения.

В случае, когда используется камера без трансфокатора, можно эксперименты проводить на установке, позволяющей перемещать камеру вдоль оптической оси объектива камеры . После определения точки пересечения оптической оси объектива камеры с плоскостью изображения следующим шагом является определение расстояния от центра проецирования (оптического центра) до плоскости изображения и определение коэффициента преобразования между единицами измерения на плоскости изображения и предметной системе координат.

Определение расстояния от центра проецирования до плоскости изображения и коэффициента преобразования

Для определения величины d - расстояния от центра проецирования S до плоскости изображения Π и коэффициента преобразования m между единицами измерения в картинной плоскости и предметной системе координат введем некоторые допущения: пусть известен угол тангажа V , а угол рысканья х равен нулю. Для решения этой задачи используется правильный шестиугольник, положение которого заранее известно в предметной системе координат. Данную задачу предлагается решать в два этапа:

• -    на первом этапе определяются точки пересечения трех проецирующих прямых с предметной плоскостью. Положение этих прямых обусловлено инцидентностью оптическому центру и трем точкам N^K/, K₂'. Точка N’ является точкой пересечения оптической оси с плоскостью изображения. Точки Ki’ и К₂’ располагаются на прямой, проходящей через точку N' перпендикулярно оси абсцисс картинной плоскости, которая в данном случае параллельна линии горизонта. Эти точки располагаются на одинаковом расстоянии от точки N' по обе стороны от нее;

• -    на втором этапе определяются параметры - коэффициент преобразования m и расстояние от центра проецирования до плоскости изображения d .

Приведем ход решения задач по каждому этапу.

Первый этап. Определить точку N можно воспользовавшись тем, что при центральном проецировании соблюдается равенство сложных отношений четырех точек, расположенных на соответственных прямых, инцидентных плоскости изображения Π и предметной плоскости Λ . Для этого в плоскости Π введем прямую а’ и соответствующую ей прямую, расположенную в плоскости Л a . Прямая а’ проходит через точку N' и одну из вершин шестиугольника P' 2 (рис. 6). Этих точек для построения соответственной прямой а недостаточно, так как проекция точки N в плоскости Λ неизвестна, а точке P 2 ' соответствует точка P 2 из условий проецирования. Поэтому в плоскости Π введем еще одну точку Т 1 ', которая получается в результате пересечения прямой а' с одной из сторон шестиугольника. За сторону шестиугольника можно принять сторону P 5 'P 6 ', т.е. T 1 '=(N'P 2 ') I (P 5 'P 6 '). Чтобы найти соответственную ей точку T 1 , воспользуемся равенством сложных отношений четырех точек:

(P'PJT!)

(JPT*PT. (P 5 t )*(P 6 T)

k-(P'P'T'T') - 651) ’ 6 5 1 2/   (P PT’)

Зная расчетную величину к и исходя из равенства сложных отношений четырех точек (P 6 'P 5 'T 1 'T 2 ')=(P 6 P 5 T 1 T 2 ), можно записать равенство, справедливое для предметной плоскости

_К = ( РРТТ) = ^(P 6 ^P 5 ^T 1 ) = ^(P 6 ^T 1 )*^(P 5 ^T 2 )

6 5 1 V    (P 6 P 5 T 2 )     (P 5 t )*(P 6 T 2 )

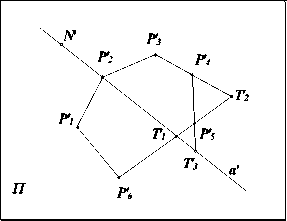
Рис. 6. Задание вспомогательных точек T 1 ',T 2 ' и T 3 ' в плоскости Π

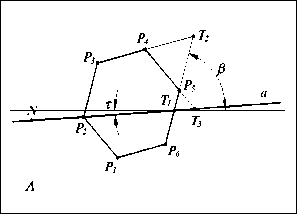
Рис. 7. Определение координаты точки N в предметной системе координат

После нахождения точки T 1 найдены только две соответственные точки на прямых а' и а. Для установления полного проективного соответствия между этими прямыми необходимо определить еще пару соответственных точек T 3 ' и T 3 .

n=(NP'T'T') = (N ^{PT) n (NP}2^{T T}3⁾ (N' P₂ T)

(N' T₁ )*(P *₂ T¹’) (P₂' T₁ )*(NT 3₃ )

Установив проективное соответствие между точками прямых а' и а, можно определить положение точки N, исходя из равенства сложного отношения четырех точек

( np2 tt)

= n = ( NP 2 T 1 T 3 ) =

(NP 2 T 1 ) (NP 2 Т з )

(NT )*(P 2 T 3 ) (P 2 T 1 )*(NT ’ )

Помимо координаты точки N, для дальнейших расчетов, необходимо определить расстояние от точки N до прямой r (рис 8), прямой, являющейся линией пересечения картинной и предметной плоскостей. Методика определения положения этой прямой приведена ниже. Для определения этого расстояния вводятся точки K1' и K2' на картинной плоскости, которые располагаются на прямой c', проходящей через точку N' и перпендикулярной прямой r. Причем эти точки K1' и K2' расположены на одинаковом расстоянии и находятся по обе стороны от точки N'. Прообразы точек K1' и K2' строятся в предметной плоскости Λ аналогично точке N (рис. 8).

Прямая c, инцидентная точкам K 1 и K 2 , будет ортогональна линии пересечения плоскости Π и Λ , то есть, другими словами, прямая, перпендикулярная K 1 и K 2 , покажет направление искомой линии пересечения плоскостей Π и Λ в предметной плоскости. Для определения точки, через которую проходит линия пересечения плоско

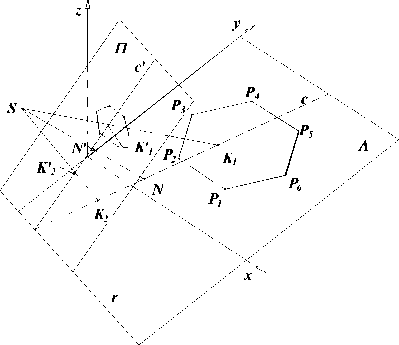
Рис. 8. Задание точек K 1 ' и K 2 ' в плоскости Π и определение прообразов этих точек в плоскости Λ

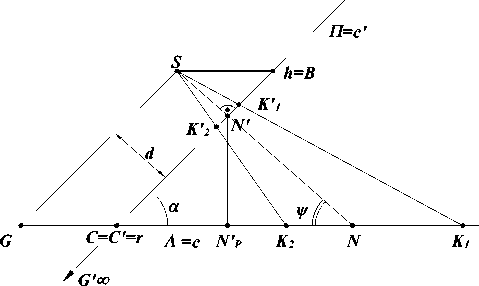
Рис. 9 Определение линии пересечения плоскостей Π и Λ

На этом рисунке плоскости Π и Λ занимают проецирующее положение, линия пересечения r плоскостей Π и Λ совпадает с точкой G. Глядя на рисунок 9, можно также установить, что точка G, ле- жащая на прямой c, является прообразом бесконечно удаленных точек G∞ прямой c'. Точка B является точкой пересечения прямой c' и линии горизонта h. Из этого рисунка видно, что на c' имеется гармоническая четверка N'G∞'K1'K2'. Соответственно, и на прямой c имеется гармоническая четверка NGK1K2. Исходя из того, что четверка точек NGK1K2 является гармонической, можно определить положение точки G по формуле:

(NGK 1 K 2 )

(NK i )*(GK 2 ) =- 1 (GK i )*(NK 2 )

Второй этап. Определение расстояния от центра проецирования до плоскости изображения и коэффициента преобразования между единицами измерения в картинной плоскости и в предметной системе координат. Для этого проведем прямую, проходящую через точку N параллельно прямой r.

z

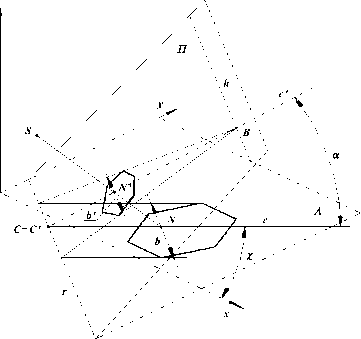
Рис. 10. Определение расстояния от центра проецирования до плоскости изображения и коэффициента преобразования между единицами измерения в картинной плоскости и в предметной системе координат

Данная прямая будет пересекать стороны шестиугольника в двух точках, расстояние между этими точками обозначим через b, а расстояние между соответствующими точками на изображении через b' (рис. 10). Из подобия треугольников следует b'm SN'

b SN , где    SN' = d, а SN = GN*cos(ψ).

Отсюда можно выразить d d = b'mdGN * cos(y) b                                                      (1)

Для определения коэффициента преобразования m воспользуемся равенством сложных отноше ний четырех точек (рис. 9)

(CNK 2 K 1 ) = (C'N'K 2 ‘K i ')= к.

Из этого равенства сложных отношений четырех точек получим квадратное уравнение m2(c3c6 - rc3+c4сб+г-4) + т(С1 Г-С1 c6-c3c5—2c6 -

-r 2- 4C5)+ C1C5 + C2C5   0 , где с 2 = K2 N(SN + NK1 cos (y)) = K 2 Nb' GN* cos (y)

b *c 5 b

c. = NK 1 (SN - K ₂ N cos (^)) = NK 1 b' GN* cos ( y )

c5 = GN*sin( y),

Коэффициентом преобразования m будет корень, который имеет положительное значение. После того как нашли m, можно определить d, подставив m в формулу (1).

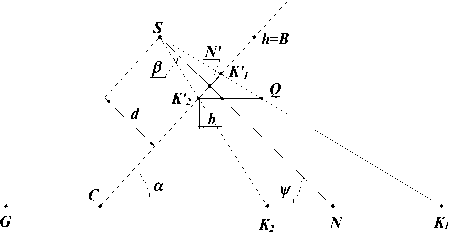
Рис. 11. Определение угла тангажа ψ

Для определения угла тангажа v рассмотрим рисунок 11, где расстояние N'K'1=NK'2= r , тогда расстояние b можно определить по формуле:

b =—

.

cos ( a )

Из треугольника CNN' (рис. 11) видно, что угол а можно выразить через угол тангажа v Pi a=т - У , ctg(a) = ctg I tg(W) = -

K 1 K ₂*r*m

( 2*NK 1 - K 1 K 2 )*d

.

Если в полученное выражение подставить d из (1), тогда окончательная формула для определения угла тангажа v будет иметь вид:

sin ( у ) = -

K 1 K ₂*r*b

(2*NK 1 - K 1 K 2 )*GN*b '

.

Вычислив значение угла тангажа v по формуле (2) и решив систему уравнений, определим искомые значения d - расстояние от центра проецирования до плоскости изображения и коэффициента преобразования m между единицами измерения в картинной плоскости и в предметной системе координат.

Определение смещения системы координат камеры и углов поворота относительно системы координат предметного пространства

Задача внешней калибровки камеры сводится к определению смещения системы координат камеры и углов поворота относительно системы координат предметного пространства. Калибровку можно осуществить, опираясь на те же выкладки, что использовались в предыдущем параграфе. Данную задачу предлагается решать также в два этапа: на первом этапе определяется направление линии пересечения плоскостей картинной и предметной в картинной плоскости; на втором этапе определяются смещения системы координат камеры и углы поворота относительно системы координат предметного пространства.

Решение задачи первого этапа. Линия пересечения предметной и картинной плоскостей всегда будет располагаться параллельно линии горизонта h, построенной в картинной плоскости. Известно, что линия горизонта является образом несобственной прямой предметной плоскости. Основываясь на этом факте, можно утверждать, что для определения линии горизонта необходимо найти в картинной плоскости точки, прообразы которых в предметной плоскости находятся в бесконечности. Предлагается за такие точки принять точки пересечения параллельных сторон шестиугольника. Образы таких сторон шестиугольника на изображении не будут пересекаться только в том случае, если предметная плоскость окажется перпендикулярна оптической оси объектива телевизионной камеры. В этом случае задача калибровки телевизионной камеры значительно упрощается. Этот случай будет рассмотрен ниже.

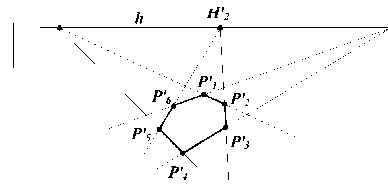
Для определения прямой h достаточно двух точек, т.е. достаточно использовать только две пары параллельных сторон шестиугольника или же вообще вместо шестиугольника использовать квадрат. Проведенные нами эксперименты показали, что линия горизонта, построенная по двум точкам, определяется менее точно по сравнению с линией горизонта, вычисленной как результат аппроксимации трех образов несобственных точек. Точки Н 1 ', Н 2 ', Н 3 ', определяющие линию горизонта, вычислялись как точки пересечения образов параллельных сторон многоугольника (рис. 12).

В нашем случае когда угол крена ф равен нулю, то линия горизонта будет параллельна оси v плоскости изображения.

Решение задачи второго этапа. Точки N, К 1 , К₂ и G можно определить, воспользовавшись методикой, приведенной ранее на с. 60. Только точки К/, K₂’ строятся на прямой, перпендикулярной линии горизонта h .

Угол тангажа у - это угол наклона оптической оси объектива к предметной плоскости. Для его вычисления сначала необходимо определить угол наклона между картинной и предметной плоскостями, обозначенного через - а (см.рис. 9).

H' 1        h      H	' 2                       H' 3
P' 1 P' 6 P' 5 P' 4 п	P' 2 P' 3

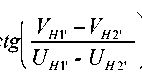
окон или фильтров). Обычно маска представляет собой небольшую (например, размерность 3x3) двумерную систему, коэффициенты которой выбираются таким образом, чтобы обнаружить заданное свойство изображения. Для понижения шума, подавления импульсных помех нами были использованы низкочастотные фильтры. Низкочастотная фильтрация изображений позволяет сглаживать изображения в заданной окрестности, чаще всего используется окрестность 3х3. Низкочастотный фильтр подавляет высокие частоты и пропускает низкие частоты. Чтобы четко определить границы зерна, необходимо также повысить резкость изображения и улучшить изображение отдельных деталей, для этого применяется высокочастотный фильтр.

Рис. 13. Исходное изображение

Рис. 14. Обработанное изображение

Определение порога бинаризации и бинаризация изображений

После предварительной обработки цифровых изображений необходимо определить порог бинаризации, который определяется из гистограммы интенсивности (рис. 15). Гистограмма интенсивности показывает количество пикселов определенной интенсивности на цифровом изображении. При этом интенсивности пикселов объекта и фона разделяются на две выделяющиеся части согласно рисунку 15. Одним из очевидных путей отделения объектов от фона является выбор порогового значения, которое определяется по гистограмме. Для выделения на изображении зерен необходимо произвести бинаризацию цифрового изображения по найденному порогу бинаризации (рис. 16).

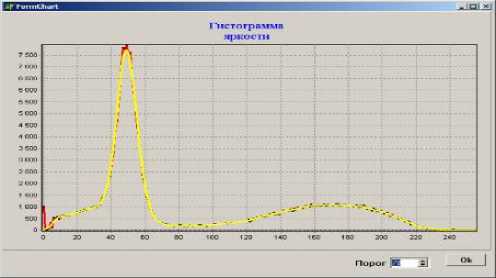
Рис. 15. Определение порога бинаризации

Рис. 16. Бинаризация изображения

Сегментация цифрового изображения

Для решения задачи сегментации цифрового изображения, т.е. определения границ зерен и выделения отдельных зерен на изображении, был применен метод сигнатуры (рис. 17), которой хорошо работает для выпуклых объектов, которым и является зерно. В результате решения задачи сегментации определены геометрические параметры каждого зерна – длина, ширина, толщина и геометрическая форма, а также цвет зерна (рис. 18). В случае нахождения дефектных зерен или посторонних включений программа управления системой сортировки зерна удалит эти дефектные зерна и примеси. По полученным данным производится статистическая обработка – определение средних, максимальных и минимальных значений.

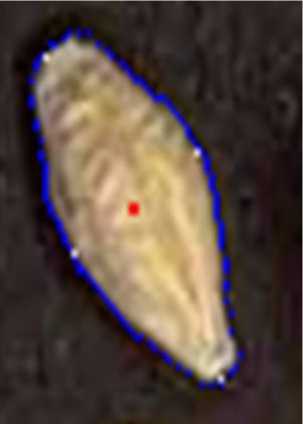
Рис. 17.. Определение границы отдельных зерен

Рис. 18. Сегментированное изображение