Программное средство для автоматизации моделирования профиля оптической поверхности

Постановка задачи . Технологический процесс производства полимерной оптики для систем отображения информации, в частности для проекционных оптических систем на основе DMD- и LCD-модуляторов изображения [1], предусматривает контроль формы асферической поверхности. Контроль формы поверхности в условиях массового производства, как правило, сводится к измерению в двух взаимно перпендикулярных направлениях величины отклонения DX ( У ) =REALX ( У ) - X ( У ) реального профиля поверхности (стрелки поверхности) REALX ( У ) от расчетного профиля X ( У ) ( У - расстояние от оси симметрии поверхности). Расчетный профиль асферической поверхности описывается выражением вида [2]

X (У) --.          — + АУ4 + B У6 + СУ8 + D У10 + E У12,         (1)

’ ^R 1 + 71 - ( 1 + K )( У/R ) ²

DX

Y

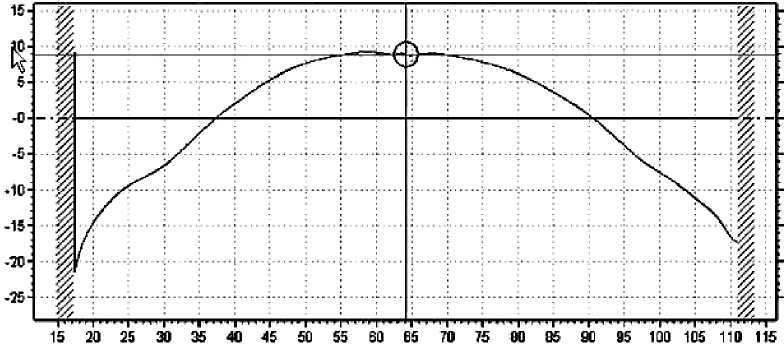
Рис. 1. График функции DX ( У )

где значения величин R , K , A, B , C , D , E определяются в процессе автоматизированного проектирования оптической системы требуемыми фокусным расстоянием и аберрационными свойствами асферической поверхности. На рис. 1 представлены результаты измерения величины отклонения DX ( У ) асферической поверхности диаметром 92 мм, полученные в графическом виде на контактном профилометре Taylor - Hobson Form Talysurf с использованием программного обеспечения pltra Software.

Графическая и табличная формы представления функции DX ( У ) малопригодны для непосредственного анализа влияния измеренных отклонений профиля на качество изображения оптической системы, элементом которой является контролируемая асферическая поверхность. В связи с этим представляется целесообразным аппроксимировать функцию REALX ( У ) выражением вида (1). В этом случае анализ влияния измеренных отклонений может быть выполнен путем замены расчетной поверхности реальной асферической поверхностью, содержащей ошибки изготовления, непосредственно в математической модели оптической системы, реализованной с помощью одной из программ автоматизированного проектирования оптических систем (CODE V, Zemax).

Аппроксимация функции REALX(У) выражением вида (1) и оценка ошибок контролируемой поверхности обычно выполняются с помощью трудоемких неавтоматизированных вычислений. Предлагаемая в настоящей работе технология и разработанное на ее основе программное средство PROFILE позволяют автоматизировать этот процесс и существенно уменьшить продолжи тельность технологического этапа.

Описание метода . Аппроксимация функции REALX ( У ) выражением вида (1) может быть выполнена следующим образом.

Известна табличная функция DX (У), по которой нетрудно восстановить REALX(У) = DX(У)-X(У) , т. е. получить таблицу (¥i,REALX(¥i)), i = 1,..., m. Восстановим модель вида (1), приближающую реальную кривую REALX (У). Для этого применим метод наименьших квадратов т                             2т

F(с) = 7£(X(c,Y)"REALX(Y)) = T£f,(c) ^min.(2)

• 2 i-I

Отсюда можно найти коэффициенты модели (1)

c = ( R , K , A , B , C , D , E ) ^т.

Здесь m - число точек; REALX ( Y ) — измеренные данные; X ( c , Y ) — теоретическая модель; ^{f (} c ^{) =} ( ^f . ⁽ c ⁾ ,..., ^fm ⁽ c ) ) ^т .

Для отыскания минимума функции (2) применим квазиньютоновский метод [3], согласно которому система уравнений для расчета направления поиска минимума на очередной k -й итерации имеет вид

(J (ck )т J (ck ) + S (ck )) Pk = -VF (ck).

Здесь J (c ) - матрица Якоби функции f (c); VF (ck) = J (ck )т f (ck); S (c) - аппроксимация по m секущим матрицы £ f (c )V2 f (c) , вычисляемая по формуле i=1

'0,

S, ,=^           1                       1        _(3)

k+1  Sk - ——-WjmXV. +—yk^, k * 0,

I     P k W k P k             Ук P k

W k = ^J ( ^ck + 1 ) ^{т J} ( ^ck ) ^{+ S} ( ^ck ) , Ук = ^J ( ^ck + 1 ) ^{т f} ( ^ck + 1 )^{- J} ( ^ck ) ^{т f} ( ^ck ) .

Если матрица H ( c_k ) = J ( c_{k + 1} ) ^т f ( c_{k + 1} ) + S ( c_k ) положительно определена, то при вычислении S ( c_{k + 1} ) по формуле (3) матрица J ( c_{k + 1} ) ^т J ( c_{k + 1} ) + S ( c_{k + 1} ) также будет положительно определена. Это означает, что на поздних итерациях метода, когда J ( c_{k + 1} ) и J ( c_k ) различаются незначительно, сохранность положительной определенности матрицы системы для расчета направления поиска обеспечена. Однако в начале вычислений матрица H ( c_k ) может получиться не положительно-определенной и направление P_k не будет являться направлением спуска. Чтобы избежать этого, модифицируем метод следующим образом.

• 1.    На каждой итерации в матрицу H ( c_k ) вносим возмущение и делаем ее положительноопределенной, т. е. полагаем H ( c_k ) = H ( c_k ) + q_kI , где q_k = 0, если H ( c_k ) положительно определена и хорошо обусловлена, q_k >  0 в противном случае. Значение q_k >  0 выбирается таким образом, чтобы оно незначительно превышало наименьшее значение q , при котором матрица H ( c_k ) + qI будет положительно-определенной и хорошо обусловленной и P_k станет направлением спуска.

• 2.    В результате возмущения матрицы H ( c_k ) шаг вдоль направления P_k может оказаться очень большим, поэтому уменьшения значения функции может не произойти. В этом случае

  
  
  
  

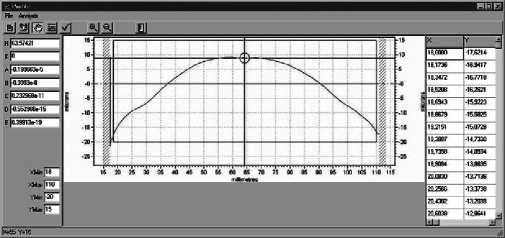
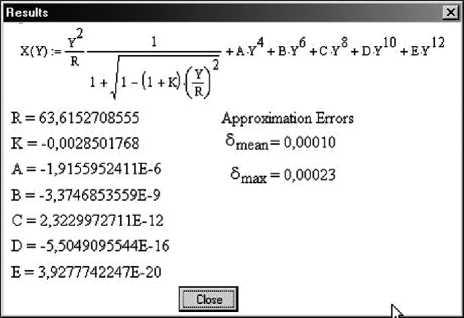
  Рис. 2. Исходные данные для аппроксимации Рис. 3. Результаты работы приложения PROFILE

  
  

применяем следующую стратегию линейного поиска с дроблением шага [4]. Зададим а е (0, 0,5), 0 < l < и < 1. Выберем коэффициент дробления gk = 1 и будем уменьшать его, если необходимо, следующим образом. При F (ck + gkpk )> F (ck) + agkVF (ck )т pk будем полагать gk = bgk для b е [l, и ]. После нахождения приемлемого gk положим окончательно ck+i = ck + gkPk.

Квазиньютоновский метод, описанный выше, обладает достаточно хорошей сходимостью и может быть использован для аппроксимации функции REALX ( У ) выражением вида (1).

Реализация метода . Предлагаемый метод программно реализован в приложении PROFILE, предназначенном для аппроксимации реального профиля асферической поверхности выражением вида (1). Исходными данными для работы приложения являются результаты измерения величин отклонения DX ( У ) =REALX ( У ) - X ( У ) реального REALX ( У ) профиля поверхности от расчетного X ( У ). Допускается представление функции DX ( У ) в графической или табличной форме. В случае графического представления в приложении предусмотрена возможность выбора значимого для аппроксимации участка кривой DX ( У ).

Результатами работы приложения являются значения величин R , K , A, B , C , D , E, которые далее могут быть использованы при анализе допустимости измеренных отклонений с помощью одной из программ автоматизированного проектирования оптических систем (CODE V, Zemax).

Исходные данные для аппроксимации и результаты работы приложения PROFILE показаны на рис. 2, 3 соответственно.

Заключение. Аппроксимация профиля асферической поверхности выражением вида (1) и оценка отклонений контролируемой поверхности обычно выполняются с помощью трудоемких неавтоматизированных вычислений. Предлагаемый в работе метод позволяет автоматизировать этот процесс и существенно уменьшить время обработки технологических данных. При использовании неавтоматизированного подхода время расчета ошибок обработки одного профиля составляет приблизительно пять дней. Полуавтоматизированный расчет с использованием математического пакета MathCAD продолжается примерно 1 ч и требует высокой квалификации инженера. Разработанное приложение PROFILE полностью автоматизировано и позволяет решить поставленную задачу за 1-2 мин. Результаты работы приложения могут быть использова- ны при анализе допустимости измеренных отклонений с помощью одной из программ автоматизированного проектирования оптических систем (CODE V, Zemax).