Программное управление движением робота с дифференциальным приводом при разных моделях трения

Original article

Software Control of the Movement of a Differential Drive Robot for Different Friction Models

Maksim S. Salimov B , Igor V. Merkuryev

Introduction . Designing motion control systems for mobile robots requires the construction of mathematical models. Researchers have repeatedly addressed this topic. In particular, works have been published on the calculations of multiphysical processes, modeling the movement of various types of wheels under certain conditions. In addition, the dynamics of deformable contacting bodies during sliding, rolling and rotation, issues of autonomy and controllability of mobile robots were considered. Note, however, that the dynamics and positioning accuracy of wheeled robots is largely determined by friction. The literature does not present studies on the dynamics of a robot with a differential drive taking into account the interrelationships of sliding, spinning and rolling friction effects based on the theory of multicomponent friction. Research in this area can reveal new dynamic effects. Based on the data obtained in this way, it is possible to improve the accuracy of positioning in building mathematical control models. The presented work aims at investigating the movement of an automatic device with a differential drive taking into account three contact models: nonholonomic, Coulomb friction, and multicomponent models.

Materials and Methods . The scheme of a two-wheeled robot with differential drive and continuous movement on the support surface was adopted as the basic one. The movement of the device was provided through software control. The dynamics was described in the form of Appel equations. Mathematical models were used for calculations, taking into account friction in different ways. Coordination of the actions of the mechanism was formed at a dynamic level. The control actions were the moments of the wheel motors. When visualizing the models under study, the built-in numerical methods of the Wolfram Mathematica system were used with a minimum accuracy of 10^-6.

Results . When building a mathematical model, the equations for the angular velocities of the wheels were determined. The authors took into account the presence of a contact site and derived the equations of dynamics of a differential drive robot. The elements of the system were force and moment projections, indicators of platform spin, masses, angular accelerations, and inertia of the wheels. It was shown how control actions were formed within the framework of nonholonomic mechanics. The model of engines that created a moment of control on the driving wheels was described. The solution was derived as the relationship between the inductance of the conductors of electric motors and the operation of the power supply. Three models describing the dynamics of a differential drive robot were examined in detail. The first model was nonholonomic. The second and third included a system of equations for the dynamics of a differential drive robot for a general case with a contact platform. At the same time, in the second model, the switching time in the engine was ignored and the Coulomb friction was involved. In the third model, a parameter to determine the speed of transients in the engine was introduced, and Pade decomposition was involved. This was a model with multicomponent friction. The calculation results were shown in the form of graphs. On them, the studied models were visualized in the form of curves of different colors. Comparison of the graphs showed in which cases, after the completion of transients, the control provided the required accuracy. These were models 1 and 2. In model 3, the

Механика

software control generated an error in the angular velocity of rotation of the platform. This error could not be predicted within the framework of the 1st and 2nd models. In all the systems considered, the sliding speed of the wheels in the transverse direction dropped to zero. The condition of continuous motion of the support wheel was obtained and validated.

Discussion and Conclusion . Software control is acceptable in models that do not take into account wheel friction during simultaneous sliding, spinning and rolling (general case of spatial motion). However, it is important to consider the relationship between these processes and multicomponent friction. This is required for the robot to perform program movements more accurately. It was established that software control in a model that takes into account the friction of spinning and rolling caused deviations from the program values of the angular velocity of the platform. The results obtained can be used in the building of a control system with predictive models.

Введение. В современном мире растет востребованность автоматических мобильных колесных аппаратов, активно исследуются возможности координации их работы. Значительный научный и прикладной интерес имеют вопросы автономности и управляемости мобильных роботов. В частности, рассматриваются подходы к расчетам мультифизических процессов, моделированию движения конкретных видов колес в разных условиях. Некоторые изыскания фокусируются на динамике деформируемых контактирующих тел при скольжении, качении и вращении. Результаты этих исследований находят применение в робототехнике [1–3]. Управление мобильными колесными аппаратами рассматривается на примере электрических самокатов «Сигвей» (Segway) [4].

Мобильные механизмы с простыми и эффективными системами управления движением колес нужны в первую очередь для работы в узких пространствах [5], для проведения исследований в сложных промышленных условиях [6].

В [7–11] показаны возможности точного моделирования динамики колесных аппаратов с учетом скольжения, верчения и качения колес.

При этом в литературе не описаны явления, возникающие при комбинации эффектов трения. Цель представленной работы — исследовать влияние поликомпонентного трения на динамику робота с дифференциальным приводом. Задачи: построить математическую модель движения робота с поликомпонентным трением и смоделировать программные движения.

Материалы и методы. Рассматривается схема двухколесного робота с дифференциальным приводом (рис. 1). Предполагается безотрывное движение колес радиуса R по опорной поверхности.

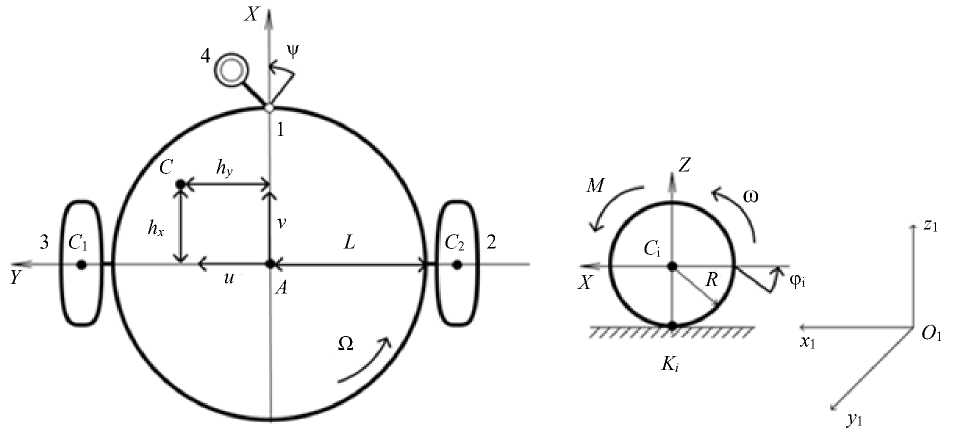
Рис. 1. Кинематическая схема робота: а — платформа; б — одно из ведущих колес

Центр тяжести платформы C смещен относительно геометрического центра платформы A по оси X на расстояние h_x , по оси Y — на расстояние h_y . Точки C ₁ и C ₂ — центры масс колес (индекс 1 соответствует левому колесу, индекс 2 — правому).

Вводятся следующие обозначения: т, — масса платформы робота; ]Cz — момент инерции платформы относительно центра масс C; O1,x1,y1 — неподвижная система координат; xA, yA определяют положение точки A в O,, x,, у,; v — угол курса платформы; фi — углы поворота колес (индекс 1 соответствует левому колесу, индекс 2 — правому); AC, = AC2 = L — расстояние между колесами; M 1,M2 — моменты двигателей, приложенные к колесам.

Предполагается, что на опорное колесо 4 (рис. 1) действует только нормальная реакция опоры. Во время движения опорное колесо располагается на оси X на расстоянии R 0 от центра платформы ( R 0 <  L ).

Результаты исследования

Математическая модель динамики робота. При описании движения робота с дифференциальным приводом в рамках неголономной механики применяются выражения, которые учитывают ограничения, связанные с отсутствием скольжения колес по отношению к поверхности:

^u к , x = 0, ^u к ₂ x = 0, ^u к , у = 0, ^u к ₂ у = 0,                                            ⁽¹⁾

где иK,иK,иK,иK^y — проекции на оси Хи Y скоростей точек K1 иK2, являющихся центрами площадок контакта колес с опорной поверхностью.

Отметим, что для неголономной модели предполагается точечный контакт колес с поверхностью, т.е. площадка контакта каждого колеса вырождается в единственную точку контакта.

Рассмотрим выражения:

и  = и - Q L - R ю,,

K ₁ x                         1

и Kx = u + O L - R ю₂,

^U K , y = ^U K 2 у = ^U Су = u .

С их помощью можно получить равенства для угловых скоростей колес:

ω1

и- О L

R

,Ю 2 =

u + Q L

R

В общем случае, когда предполагается наличие площадки контакта, получим уравнения динамики робота с дифференциальным приводом:

т, |u - hyО - О (u + hxО)J + 2тк (и - Оu) = F cos а, + F cosa2 - F sin а, - F±2 sin a2, m,|u + hxО + О (и - hyО)J + 2mK (u + Ou) = F sin a, + F sin a2 - F^ cos а, - F^ cos a2,

О ( J_Cz + 2 J Kz + m , ( h x + h y 2 ) + 2 m_KL ² ) + m , [ ( u + O u ) h_x - h y ( u - О u ) J =

M„ + M„ + ( F cos a. - F. sin a, - F cos a, + F. sin a, ) L, C1          C 2          I,            2        x2           2        I,            ,        xt

J co, = M. - M„ - F cos a, - F. sin a R, Ky !           !          y,          I,            !        ^,

J„ d>, = M, - M - F cos a. - F sin a. ) R .

Ky 2        2        y2        12         2      ^2

Здесь F , F — проекции силы трения на направления скоростей скольжения центров пятен контакта колес;

F _± , F _±2 — проекции силы трения на направления, перпендикулярные скоростям центров пятен контакта колес; Mc^ , М_Сг — слагаемые момента трения при верчении для двух колес; ii — угловое ускорение верчения платформы; ю , ,< в ₂ — угловые ускорения колес, проецируемые на их ось вращения; m_K — масса каждого колеса; J_Ky и J_Kz — моменты инерции колеса относительно соответствующих осей.

Для формирования управляющих воздействий будем использовать модель динамики робота, описанного в рамках неголономной механики [12]:

Механика

^{2 J}Ky . M i + M₂

m, I u - h О - О h О I + 2 m u + —f-u = —!-----, i l y         x J к ^2

m1 [(+hxQ + Q (u- hyQ)) hx - hy (u - hyQ - QhxQ)] +

²      ( M, - M. ) -

Q(JCz + 2Jк, + mi (hx + hy2) + 2mL) + 2JR Q = ( 2 R 17

Ее также можно представить в виде:

F = M i + M_: ^u —

2. _M    ( ^M 2 - ^M 1 ) ^—

, M Q

R

,

где F _u и M _Q — левые части уравнения (5).

Модель двигателей на ведущих колесах. Опишем модель двигателей, способных генерировать момент управления на ведущих колесах M ₁, M ₂.

Уравнения движения колесных двигателей постоянного тока можно выразить формулами [13]:

_T d ( i k )         _

L_e — -- + —i_k = Uk - C i ^ю,,

e dt

M k = c 2 i k , ( k = 1,2 ) .

Здесь L_e — индуктивность проводников электродвигателей; R — сопротивление электрическому току в цепи двигателя; U_k — электропитание для двигателя k ; _k — ток, проходящий через цепь якоря двигателя; c ₁, c ₂ — конструкционные постоянные двигателей.

Предполагается, что двигатели ведущих колес имеют одинаковую характеристику. Из (7) видно, что

Mk ik               .

c ₂

Учитывая (8), в первом уравнении из системы (7) получим дифференциальное уравнение относительно момента M : к

Уравнение (9) разделим

на множитель

L

• —M M k + — M k = U k

c ₂ R c ²

c ₂

• ^- c 1 “ k .

и получим:

Lc         c

Mk + Mk =  Uk c2R           R

cc

--ш.

Rk

Введем обозначения:

L          c,Cz e2         12         2

T. =---- , к =--- , к, = —

¹ c ₂ R ¹ R ² R

В таком случае управляющие моменты можно описать:

т_гм_к + M_k = KU - K ш,, 1 kk 2 k 1 k

.

где K ₁, K ₂ — константы; T ₁ — параметр, определяющий скорость переходных процессов в электрической части двигателей.

При игнорировании времени переключений в электромеханической системе двигателя:

M k = K 2 U k - K 1 Ш k .

Авторы [14] получили похожие формулы.

Исследуемые модели . Рассмотрим модели, описывающие динамику робота с дифференциальным приводом.

Модель 1 описывается уравнениями (6) и (12), когда длительность переходных процессов полагается исчезающе малой T 1 = 0 :

2 J    KU

m. Ги - hv Q - Q hx Q1 + 2 mK u + —u =----

1    yx    к   R 2

- K 1 ^ 1 + K 2 U 2 -

K ₁ω₂

,

mi [( +hxQ + Q (u- hyQ )) hx - hy (u - hyQ - QhxQ)]

+Q( J  + 2 Jк, + mi (hx + hy2) + 2m^L2) =

R

L ²

+ 2 J_K —— £Q +

Ky R 2

( ( K ₂ U ₂ - K 1 to ₂ ) - ( K ₂ U 1 - K 1 to 1 ) ) L

R

.

Здесь ω1, ω2 вычисляются по формулам (3).

Для описания модели 2 применяются уравнения (4), (13), а также модель трения Кулона: F =- fN, F^ = 0, Me, = 0.

Модель 3 представлена уравнениями (4), (12). представленное в [12] с помощью разложений Паде:

Кроме того, учитывается поликомпонентное трение,

* Ky + k r 1 1 1 Q

2 1. - k L cos ^П - a

¹ r ² V 2

F=- fN.

I 0

I n cos - a

2 I, - k,L cos ^П - a 1 r 2

V ^ + uKy +------7     2 Q

I ₀

F l

- fN,

k_r πΩ

MC

2 I 1 k r I 1 I 2

=- 2 f n 1 2

I n

- k L cos - a r 2 I 2

I 0

cos

,

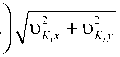
I П 1

k L cos - a r 3 i i

V2   2

² - к cos

I

^{2 1} 2         V ¹ 3

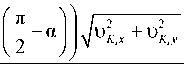
2I2           । n 11 n : 2

k- cos   -a u^- +U- + Q r                     K x K y

. ¹ з              ^{V 2      2}2

ω

M _± =^- k ^п I 3 -. _ω

Здесь I ₁, I ₂, I ₃ — постоянные величины, которые находятся по формулам в [12]; α — угол, характеризующий

направление линейных скоростей скольжения относительно точек контакта колес K ₁, K ₂; k_r — коэффициент, знак которого зависит от направления качения.

Для определения программного управления следует указать законы движения робота u d ( t ) , Q d ( t ) . По (5) можно выразить величины F _u = F Q d ( t ), F _u = F Q ( t ) , M _Q = M Q ( t ) в зависимости от времени. Используем

известные значения F _u , M _Q для вычисления управляющих напряжений U 1 и U ₂, подаваемых на приводы колес:

и₂ = — | - 1 F + M ^ |+ к ш₂

²   K ₂ V 2 V ^й L J ¹²

, U = — I R | F - M ^ |+ к to! I .

1   K2 V2V u L J 112

Движение системы с заданными начальными условиями

u ( 0 ) = 0,5 — , u ( 0 ) = 0,2 м , Q ( 0 ) = 0,2 -

смоделировали в математическом пакете «Вольфрам математика» (Wolfram Mathematica).

Рассмотрим u d ( t ) = 0,5 — , Q d ( t ) = 0,3 1. Для интеграции системы автоматически выбирали шаг

c

c

интегрирования и задействовали встроенные численные методы Wolfram Mathematica с точностью результатов не менее 10–6.

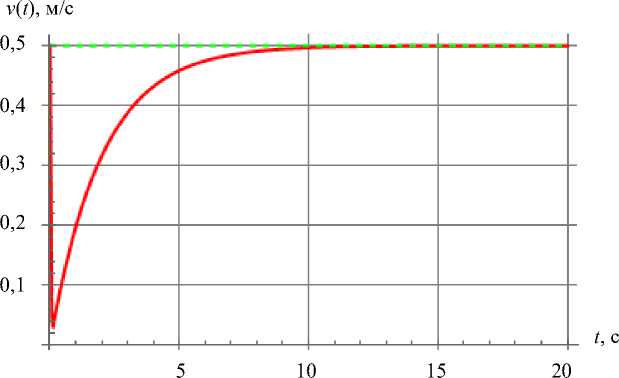
Рис. 2. Зависимость продольной скорости и . Зеленая кривая — неголономная модель 1, красная кривая — модель 2 с трением Кулона, синяя кривая — модель 3 с поликомпонентным трением.

Синяя и красная кривые совпадают

Механика

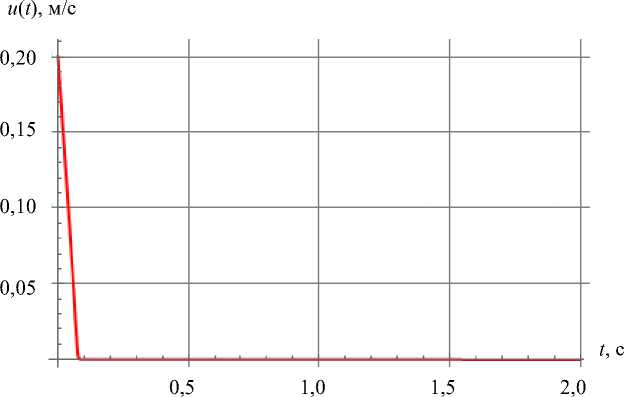
Рис. 3. Зависимость поперечной скорости и. Зеленая кривая — неголономная модель 1, красная кривая — модель 2 с трением Кулона, синяя кривая — модель 3 с поликомпонентным трением.

Зеленая, синяя и красная кривые совпадают

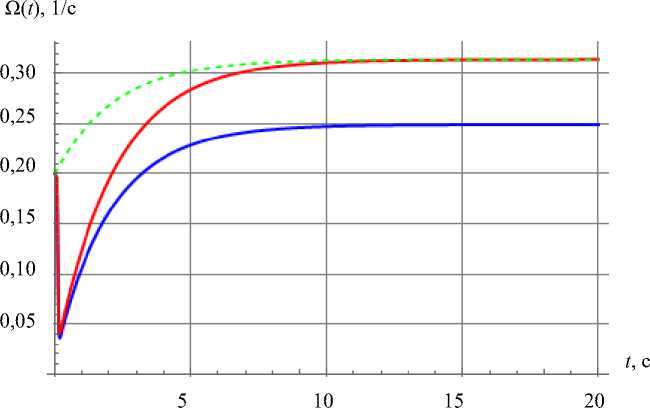
Рис. 4. Зависимость угловой скорости робота. Зеленая кривая — неголономная модель 1, красная кривая — модель 2 с трением Кулона, синяя кривая — модель 3 с поликомпонентным трением

Из рис. 2 и 4 видно, что управление гарантирует точную реализацию программных законов движения после завершения переходных процессов в моделях 1 (неголономная) и 2 (с трением Кулона). В модели 3 (поликомпонентное трение скольжения, качения и верчения) после завершения переходных процессов из-за программного управления возникает постоянная ошибка в угловой скорости вращения платформы. Во всех рассмотренных моделях скорость скольжения колес в поперечном направлении быстро снижается до нуля. Случаи совпадения зависимостей, полученных для разных моделей, показаны на рис. 2 и 3.

Для проверки выполнения условий безотрывного движения опорного колеса запишем теорему изменения кинетического момента системы в проекциях на ось Y :

J „ (co. + co,) = M . + M, - M - M  - N-,R_n + m,gh - F„ cos a. - F. sin a. + F cos a, - F. sin a, ) R .

Ky 1        2            1          2 У 1           У 2         3 0         1 X          |1            1         ^ i           1        |2            2         ^ 2           2

Согласно (4):

M 1 + M ₂ =- N ₃ R 0 + m₁ gh x .

Из последнего уравнения получаем условие безотрывного движения опорного колеса: m₁ gh x — ( M 1 + M 2 ) >  0.

С учетом (5):

2JK mlghx - R(ml + 2mk + ^2-)и + Rmi[hy^ + hx^ ] > 0. R

Ускорения робота не превышали 1 м/c2, поэтому данное неравенство выполняется в каждый момент времени.

Обсуждение и заключение. Итоги моделирования позволили сделать ряд выводов. Программное управление, основанное на неголономной модели 1, приемлемо для роботов, конструкция которых не учитывает контактное трение колес, возникающее при комбинации скольжения, верчения и качения. Однако при формировании управляющих воздействий для достижения более точного следования программным законам движения необходимо учитывать модель поликомпонентного трения. Полученное решение можно использовать при построении системы управления с прогнозирующей моделью (model predictive control). Такая разработка будет предметом дальнейшего исследования.