Программные генераторы в среде GPSS World для распределений вероятностных смесей и оценка их качества

Имитационному моделированию и, в частности, универсальной системе дискретно-событийного моделирования GPSS WORLD, которая широко используется при моделировании систем массового обслуживания и производственных систем, посвящено много работ [3–9]. Система GPSS WORLD включает множество библиотечных программ, в том числе генераторы псевдослучайных последовательностей для различных законов распределений.

В теории массового обслуживания востребованы законы распределений с широким диапазоном коэффициента вариации случайной величины, такие как гиперэрланговский или гиперэкспоненциальный. Как было отмечено в [1; 2], таких генераторов в системе моделирования GPSS WORLD нет, как их нет и в других системах имитационного моделирования. В [1; 2] представлены эти генераторы в качестве имитационных моделей систем массового обслуживания (СМО) HE2/M/1 и H2/M/1 соответственно на основе имеющихся в библиотеке GPSS WORLD генераторов.

Постановка задачи

В статье приводятся результаты применения статистических тестов к функционированию имитационных моделей систем HE 2 /M/1 и H 2 /M/1 в GPSS WORLD для оценки качества программных генераторов гиперэрланговского и гиперэкспоненциального распределений. Выводы об адекватности имитационных моделей систем HE 2 /M/1 и H 2 /M/1 делаются на основе статистического теста Пирсона, сопоставления теоретических и статистических моментов указанных распределений, а также сопоставления результатов имитации с известными результатами численно-аналитических моделей указанных систем в Mathcad.

Выше было отмечено, что в отличие от классических законов распределений, используемых в теории вероятностей, таких как равномерный, показательный, нормальный, Эрланга и других, для рассматриваемых нами распределений, применение автоматизированных систем для статистической проверки качества генерации псевдослучайных чисел невозможно.

Проверка гипотезы о гиперэрлангов-ском распределении псевдослучайных последовательностей (ПСП) на примере СМО HE 2 /M/1

Приведенную в [1] имитационную модель для СМО HE2/M/1 дополним блоками GPSS WORLD с приведенными ниже комментариями для фиксации длин интервалов между соседними требованиями во входящем потоке для последующего построения по ним статистического ряда и гистограммы распределения интервалов поступлений. После этого представим полную имитационную модель уже без комментариев.

Пирсона придется считать вручную. Это связано с тем фактом, что в автоматизированных программных продуктах нет рассматриваемых законов распределений. Фактически это означает, что мы берем данные для переходного режима функционирования СМО. Для установившегося режима необходимо провести несколько сотен тысяч испытаний в одном прогоне. Результаты прогона с выходными данными для статистического ряда и гистограммы представлены на рисунках 1 и 2.

Окончательная имитационная модель тогда будет иметь вид:

InterArr TABLE X$Arr,1,1,24	; Построение таблицы значений интервалов поступлений
INITIAL X$Time,0 Fun VARIABLE (AC1-X$-Time) SAVEVALUE Arr,V$Fun SAVEVALUE Time,AC1	; для статистического ряда и гистограммы ; Установка начального значения «Time» равного нулю ; Определение функции вычисления значений интервалов ; поступлений ; Внести в ячейку «Arr» число, определенное функцией «Fun»
TABULATE InterArr MARK 2	; Внести в ячейку «Time» текущее значение абсолютного ; модельного времени ; Внести содержимое ячейки «Arr» в таблицу «InterArr» ; для построения статистического ряда и гистограммы ; Внести в ячейку «2» значение текущего абсолютного ; модельного времени

FACILITY ENTRIES UTIL. AVE.TIME AVAIL. OWNER PEND INTER RETRY								DELAY 22
CHAN		501	0.980    0	.966   1	860    0	0	0
QUEUE	MAX	CONT.	ENTRY ENTRY(0) AVE.CONT.		AVE.TIME	AVE.	(-0)	RETRY
QCHAN	63	23	523	3    21.673	20.468	20.	586	0
TABLE		MEAN	STD.DEV.	RANGE    RETRY	FREQUENCY CUM.%
INTERARR		0.944	1.759	0
				- 1.000	417	79.73
			1.000	- 2.000	67	92.54
			2.000	- 3.000	10	94.46
			3.000	- 4.000	5	95.41
			4.000	- 5.000	4	96.18
			5.000	- 6.000	6	97.32
			6.000	- 7.000	4	98.09
			7.000	- 8.000	3	98.66
			8.000	- 9.000	1	98.85
			9.000	- 10.000	5	99.81
			10.000	- 11.000	1	100.00

Рисунок 1. Результаты прогона имитационной модели в виде статистического ряда

Для прогона имитационной модели установим следующие исходные данные: возьмем коэффициент загрузки р = т_ц / т_Х = 0,9, коэффициент вариации интервалов поступлений c _Х = 2 и единичное время обслуживания т^ = 1 . Отсюда параметры гиперэрланговского распределения p = 1 ₊ ²⁽¹ + c 2 ) ^- 3 = ₀,₉₁8, 1 - p = ₀,₀82,

2 N 8(1 + c 2 )

Х 1 = 3,306, Х ₂ = 0,294.

Тогда средние значения для формирования первой и второй фаз гиперэрланговского распределения будут равны 1/ Х 1 = 0,303, 1/ Х ₂ = 3,401 единиц времени. Ширину разряда для статистического ряда установим равной единице, число испытаний в прогоне возьмем N=500. Таким образом, не проводя многочисленных экспериментов мы выбрали небольшой объем выборки, равный 500, с тем, что статистический критерий

10 InterArr TABLE X$Arr,1,1,16

20 INITIAL X$Time,0

30 P_1 EQU 0.082

40 P_2 EQU (1-P_1)

50 T_1 EQU 3.401

60 T_2 EQU 0.303

70 Fun VARIABLE (AC1-X$Time)

80 GENERATE ,,,1

90 Switch TRANSFER P_1,Met_2,Met_1

100 Met_1 TRANSFER ,Kl_1

110 Met_2 TRANSFER ,Kl_2

120 Kl_1 LOGIC S Kluch1

130 ADVANCE (T_1#7.03)

140 LOGIC R Kluch1

150 TRANSFER ,Switch

160 Kl_2 LOGIC S Kluch2

170 ADVANCE (T_2#7.03)

180 LOGIC R Kluch2

190 TRANSFER ,Switch

200 GENERATE (GAMMA(11,0,T_1,2))

210 GATE LS Kluch1,Met_10

220 TRANSFER ,Met_20

230 GENERATE (GAMMA(21,0,T_2,2))

240 GATE LS Kluch2,Met_10

250 Met_20 SAVEVALUE Arr,V$Fun

260 SAVEVALUE Time,AC1

270 TABULATE InterArr

280 MARK 2

290 QUEUE QCHAN

300 SEIZE CHAN

310 DEPART QCHAN

320 ADVANCE (Exponential(31,0,1.0))

330 RELEASE CHAN

340 TERMINATE 1

350 Met_10 TERMINATE

360 START 500

Используя полученные данные статистического ряда о длинах интервалов между соседними требованиями, поступающими в систему (рис.1), определим статистику критерия Пирсона χ2. Одна из форм этого критерия имеет вид

χ 2 = ∑ ^K ( m i - p i ⋅ N )² .             (1)

i ∑ =1      p i ⋅ N

Здесь mi – число попаданий исследуемой случайной величины в i – й разряд статистического ряда I, pi – теоретические вероятности попаданий в данный разряд ti

_A = J [ pX 2 1 e ■ t + (1 - p )Ъ ?_Т t e ■ t ] dt , ti - 1

K – число разрядов, N – общее число испытаний. Если в некоторых разрядах число попаданий mi мало, то эти разряды следует объединять с соседними, чтобы тем самым исключить случайные факторы. Для данных на рисунке 1 объединим разряды с малыми значениями mi = 1 с соседними, как это показано в таблице 1.

Как известно, например из [10], статистический тест Пирсона определяет меру расхождения статистического распределения от теоретического закона распределения, в качестве которого нами выбрано гиперэрланговское распределение. Критерий (1) представляет собой случайную величину, зависящую от выбранного закона распределения, числа степеней свободы, количества разрядов статистического ряда и числа испытаний.

Для данных, представленных на рисунке 1, запишем нужные нам параметры K = 9 – число разрядов статистического ряда, N = 523 – число испытаний, определенное как число входов тран-зактов в модель (ENTRY). Все промежуточные вычисления статистики Пирсона для статистического ряда, представленного на рисунке 1, поместим в таблице 1. Результаты вычисления статистики Пирсона приведены в таблице 1.

По таблице критических значений критерия χ2 для числа степеней свободы r = 9-4 = 5 найдем близкие значения этого критерия: 4,35 с вероятностью 0,5 и 6,06 с вероятностью 0,3. Тогда линейная интерполяция нам дает вероятность P = 0,43 для значения χ2 = 4,99.

Таблица 1. Вычисления критерия Пирсона ^{χ 2}

I	m i	pi	^ 2
0-1	417	0,77626	0,299
1-2	67	0,14231	0,741
2-3	10	0,01731	0,099
3-4	5	0,00927	0,005
4-5	4	0,00847	0,042
5-6	6	0,00770	0,967
6-7	4	0,00679	0,057
7-9	4	0,01077	0,473
9-∞	6	0,02112	2,305
	∑=523	∑=1,000	∑=4,99

Эта вероятность в статистике не маленькая, поэтому полученный в ходе прогона статистический ряд не противоречит гипотезе о том, что данные значения интервалов поступлений требований в систему HE2/M/1 распределены по ги-перэрланговскому закону.

Сравнение моментов закона распределения HE2 показывает некоторые расхождения, что можно объяснить в данном случае с небольшим числом испытаний N = 523. По исходным данным, среднее значение для интервалов поступлений 10/9 = 1,111, а коэффициент вариации равен двум. Статистические моменты равны: среднее значение 0,944 (Mean), а стандартное отклонение 1,759 (Std.Dev.), что дает коэффициент вариации 1,86. С увеличением числа испытаний, такое расхождение должно будет уменьшаться.

Проверка гипотезы о гиперэкспоненциальном распределении ПСП на примере СМО H2/M/1

Имитационную модель СМО H2/M/1 на GPSS WORLD, представленную в [2] для построения статистического ряда и построения гистограммы распределения дополним теми же блоками, что и для системы HE2/M/1. Ниже представлена полная имитационная модель с учетом дополнительных блоков. Для этого случая ширину разряда статистического ряда положим равной двум, а число испытаний в прогоне – 1000. Установим для прогона исходные данные: возьмем коэффициент загрузки р = тц / тК = 0,9, коэффициент вариации интервалов поступлений cК = 2 и единичное время обслуживания тц = 1. Тогда параметры гиперэкспоненциального распреде- p = 1(1 + cK—) = 0,887 2      c 2 +1

К

ления

1 - p = 0,113 ,

К1 = 1,597, К2 = 0,203. Отсюда средние значения для формирования первой и второй фаз гиперэкс- поненциального распределения составляют

1/ К1 = 0,626 , 1/ К 2 = 4,929 единиц времени.

600         _

Рисунок 2. Полученная гистограмма распределения HE2

10 InterArr TABLE X$Arr,2,2,14

20 INITIAL X$Time,0

30 P_1 EQU 0.113

40 P_2 EQU (1-P_1)

50 T_1 EQU 4.929

60 T_2 EQU 0.626

70 Fun VARIABLE (AC1-X$Time)

80 GENERATE ,,,1

90 Switch TRANSFER P_1,Met_2,Met_1

100 Met_1 TRANSFER ,Kl_1

110 Met_2 TRANSFER ,Kl_2

120 Kl_1 LOGIC S Kluch1

130 ADVANCE (T_1#6.22)

140 LOGIC R Kluch1

150 TRANSFER ,Switch

160 Kl_2 LOGIC S Kluch2

170 ADVANCE (T_2#6.22)

180 LOGIC R Kluch2

190 TRANSFER ,Switch

200 GENERATE (Exponential(11,0,T_1))

210 GATE LS Kluch1,Met_10

220 TRANSFER ,Met_20

230 GENERATE (Exponential(21,0,T_2))

240 GATE LS Kluch2,Met_10

QUEUE MAX CONT.		. ENTRY ENTRY(O) AVE.CONT. AVE.TIME AVE.(-O)			RETRY 0
QCHAN 69	54	1054     68    18.375	21.742	23.241
TABLE INTERARR	MEAN 1.183	STD.DEV.   RANGE     RETRY 2.126                  0 -  2.000 2.000 - 4.000 4.000 - 6.000 6.000 - 8.000 8.000 - 10.000 10.000 - 12.000 12.000 - 14.000 14.000 - 16.000 16.000 - 18.000 18.000 - 20.000	FREQUENCY CUM.% 914    86.72 74    93.74 24    96.02 17    97.63 9    98.48 7    99.15 3    99.43 2    99.62 2    99.81 2   100.00

Рисунок 3. Результаты прогона имитационной модели в виде статистического ряда

250 Met_20 SAVEVALUE Arr,V$Fun

260 SAVEVALUE Time,AC1

270 TABULATE InterArr

280 MARK 2

290 QUEUE QCHAN

300 SEIZE CHAN

310 DEPART QCHAN

320 ADVANCE (Exponential(31,0,1.0))

330 RELEASE CHAN

340 TERMINATE 1

350 Met_10 TERMINATE

360 START 1000

Результаты прогона с выходными данными для статистического ряда и гистограммы представлены на рисунках 3 и 4.

Для данных, представленных на рисунке 3, запишем нужные нам параметры K = 10 – число разрядов статистического ряда, N = 1054 – число испытаний, определенное как число входов транзактов в модель (ENTRY). Все промежуточные вычисления статистики Пирсона для статистического ряда, представленного на рисунке 3 поместим в таблицу 2.

Таблица 2. Вычисления критерия Пирсона ^{χ 2}

I	m i	pi	χ 2
0-2	914	0,88851	0,540
2-4	74	0,05994	1,854
4-6	24	0,01813	1,252
6-8	17	0,01119	2,297
6-10	9	0,00742	0,178
10-12	7	0,00494	0,618
12-14	3	0,00329	0,063

14-16	2	0,00220	0,044
16-18	2	0,00146	0,138
18-∞	2	0,00292	0,377
	Σ=1054	Σ=1,000	Σ=7,36

По таблице критических значений критерия ^{χ 2} для числа степеней свободы r = K -4 = 6 найдем близкие значения этого критерия: 7,23 с вероятностью 0,3 и 8,56 с вероятностью 0,2. Степень свободы r определяется числом наложенных связей для закона распределения. К примеру, для показательного закона с одним параметром распределения r = K -2, для нормального закона с двумя параметрами r = K -3. Закон распределения H₂ включает три параметра, поэтому r = K -4. Линейная интерполяция значений критерия Пирсона нам дает для значения ^{χ 2} = 7,36 вероятность P = 0,29. Эта вероятность при проверке гипотез в статистике не маленькая, поэтому полученный в ходе прогона статистический ряд не противоречит гипотезе о том, что данные значения интервалов распределены по гиперэкспоненциальному закону.

Сравнение теоретических моментов распределения H2 с статистическими моментами показывает также некоторые расхождения, что можно объяснить в данном случае тоже с относительно небольшим числом испытаний N = 1054. По исходным данным, среднее значение интервалов поступлений 10/9 = 1,111, а коэффициент вариации равен двум. Статистические моменты равны: среднее значение 1,183 (Mean), а стандартное отклонение 2,126 (Std.Dev.), что дает коэффициент вариации 1,8. С увеличением числа испытаний можно ожидать, что такое расхождение будет уменьшаться.

В статье использованы приемы аппроксимации законов распределений с использованием моментных характеристик. Эти методы более подробно описаны в [11–16].

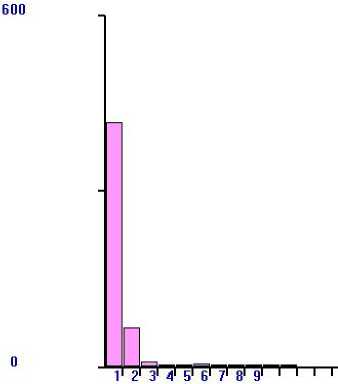
Рисунок 4. Полученная гистограмма распределения H2

Заключение

В работе представлены разработанные в GPSS World имитационные модели функционирования СМО HE 2 /M/1 и H 2 /M/1 с гиперэрланговским и гиперэкспоненциальным входным распределениями второго порядка. Представлены также результаты статистических тестов для оценки качества генерирования псевдослучайных чисел по законам HE₂ и H₂ в случае переходного режима функционирования СМО. Результаты показывают удовлетворительное качество работы соответствующих представленных генераторов ПСП.

Полученные результаты публикуются впервые.