Программный комплекс коррекции сигнала в частотной области с использованием быстрого преобразования Фурье

Прием сигналов в каналах мобильной радиосвязи затруднен из-за многолучевого распространения, которое приводит к интерференции сдвинутых во времени копий передаваемого сигнала и, как следствие, к частотно-селективным замираниям и межсимвольным помехам. Преодоление межсимвольной интерференции традиционно производится с помощью эквалайзеров (линейных и нелинейных выравнивателей) [1]. Поскольку импульсная характеристика канала непрерывно меняется, эквалайзер должен быть адаптивным. Адаптивные эквалайзеры подробно изучены и описаны в литературе [1-2]. Выравнивание сигнала при этом производится во временной области. Такие эквалайзеры работоспособны как при потоковой, так и при пакетной передаче данных.

Альтернативным способом преодоления межсимвольных помех, который анализируется в статье, является выравнивание в частотной области (FDE) [3]. Оно требует прямого, а затем обратного быстрого преобразования Фурье (БПФ), между которыми производится комплексное умножение спектральной плотности сигнала на передаточную функцию выравнивателя. Преобразование Фурье требует разбиения потока данных на пакеты, длина которых согласована с размером БПФ.

Один из методов FDE можно реализовать по алгоритму, когда передаваемые пакеты следуют плотно один за другим, образуя непрерывный поток символов. Разбиение потока на пакеты производится на приемной стороне, в результате чего образуется межпакетная интерференция, приводящая к большой погрешности выравнивания на границах пакетов. Эффективным средством борьбы с этой погрешностью является параллельная обработка одного и того же сигнала со сдвигом на с последующим сшиванием неискаженных частей пакетов [4]. Преимуществом этого метода является отсутствие необходимости введения защитных интервалов на передаче. Серьезным недостатком этого метода является удвоенный объем вычислительных операций на приемной стороне.

В статье анализируются следующие методы FDE при пакетной передаче:

• 1.    Метод пост-паузы.

• 2.    Метод циклического префикса.

В качестве имитационной модели для получения экспериментальных данных в статье использовался программный комплекс [5], разработанный в среде С++. Этот пакет программ позволяет создать модель беспроводного канала с требуемыми параметрами.

Метод пост-паузы

На рис. 1 представлен алгоритм работы метода пост-паузы. Блок Mapper выполняет функцию модулятора, на его выходе образуется сигнал, состоящий из комплексных величин. Разбиение на пакеты производится на передающей стороне с оставлением между пакетами пассивных защитных интервалов, длительность которых перекрывает временное рассеяние сигнала за счет многолучевости (см. рис. 2). На приемной стороне пауза заполняется «хвостами» от рассеяния предыдущего пакета, однако межпакетная интерференция отсутствует. Размер БПФ (FFT) охватывает суммарную длительность пакета и паузы (см. рис. 3).

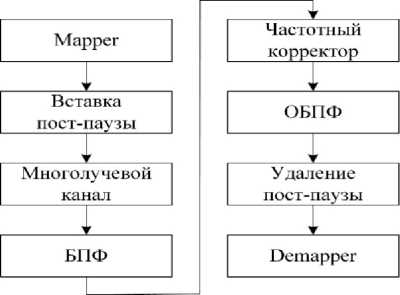
Рис. 1. Алгоритм работы метода пост-паузы

Затем принятый сигнал корректируется в частотной области и преобразуется обратно в функцию, зависящую от времени, при помощи ОБПФ (IFFT). После этого паузы удаляются. Последней операцией в алгоритме является восстановление битового потока с помощью блока Demapper. Его работа осуществляется по правилу максимального правдоподобия [1].

-                N             ---и

I-                                                    -I" 1 ,

Информационный блок |Пауза

Рис. 2. Иллюстрация метода пост-паузы (передающая сторона)

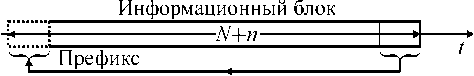
Рис. 5. Иллюстрация метода циклического префикса (передающая сторона)

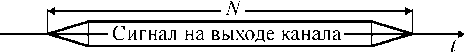
Рис. 3. Иллюстрация метода пост-паузы (приемная сторона)

Метод циклического префикса

Отличие этого алгоритма от предыдущего заключается в наличии блоков вставки и удаления циклического префикса. Разбиение на пакеты производится на передающей стороне, однако между пакетами вставляется циклический префикс, длительность которого n перекрывает временное рассеяние сигнала [6]. Префикс представляет собой фрагмент сигнала, взятый с конца пакета и скопированный в начало (см. рис. 5). Размер БПФ N охватывает только длительность пакета.

На приемной стороне циклический префикс удаляется. Как и в предыдущем методе, здесь используется корректирование сигнала в частотной области, для чего применяется БПФ. Поскольку БПФ является циклической функцией, а «хвосты» от циклического префикса накладываются на первые символы информационного блока в начале пакета, n символов в конце пакета восстанавливаются.

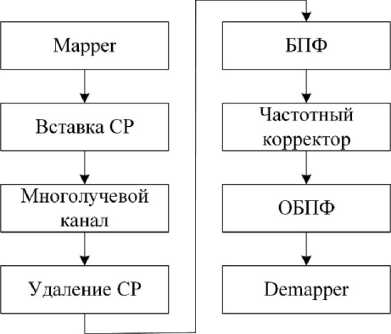
Рис. 4. Алгоритм работы метода циклического префикса

При одной и той же длине пакета метод циклического префикса более экономно использует временной ресурс, поскольку служебная информация занимает меньшую часть пакета.

— N

---Сигнал на выходе канала Интервал обработки

Рис. 6. Иллюстрация метода циклического префикса (приемная сторона)

Частотный корректор по алгоритму сведения к нулю

Нуль-форсирующий корректор [1] при отсутствии помех является простейшим типом корректора, принцип работы которого заключается в восстановлении спектра сигнала, искаженного каналом. Для этого по импульсной характеристике канала определяется передаточная функция корректора, на которую затем умножается спектр принимаемого сигнала.

Обозначая импульсную характеристику канала в виде множества {У /}’ передаточную функцию k -ой компоненты корректора можно получить по формуле:

к N-i

/=о где N – размер БПФ. Следовательно, при отсутствии шума в канале на выходе нуль-форсиру-ющего корректора восстанавливается исходный сигнал, то есть полностью устраняется МСИ. Однако при наличии шума корректор увеличивает его дисперсию. Существенным недостатком такого корректора является бесконечно большое усиление шума на частотах, где передаточная функция канала обращается в нуль. Это приведет к полному подавлению сигнала на всей временной оси. Ради справедливости заметим, что эта ситуация встречается с малой вероятностью.

Частотный корректор по минимуму среднеквадратической ошибки

Лучшие результаты показывает корректор, обеспечивающий минимизацию среднеквадратической ошибки (СКО) [1]. Если эту ошибку рассматривать как шум, то минимизация дисперсии СКО способствует снижению вероятности ошибки демодуляции.

Рассмотрим блок-схему канала с корректором (см. рис. 7), где ¹¹ ^ – сигнал на входе канала; s(t) И nU) – сигнал и шум, поступившие на вход корректора; z(f) = s(?)+ n^ – их сумма на его выходе. Задача состоит в том, чтобы минимизировать среднеквадратическое отличие 2(t) ОТ uQY то есть погрешность восстановления сигнала. Эта погрешность включает два слагаемых: погрешность восстановления самого сигнала и погрешность, обусловленную наложением шума.

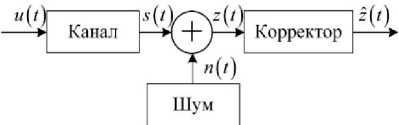
Рис. 7. Блок-схема канала с корректором

ЭХ эск5

В соответствии с рис. 1 и рис. 4 рассматриваемый корректор состоит из трех блоков, показанных на рис. 8. Для минимизации общей дисперсии ошибки необходимо минимизировать погрешность восстановления каждой k -ой частотной компоненты.

Рис. 8. Блок-схема корректора

Дисперсия погрешности восстановления k -ой компоненты сигнала равна

Dri=Dck\l-ykCk\\ где Dck – дисперсия сигнала. Дисперсия погрешности, обусловленной наложением k-ой компоненты шума, равна

^ =X<^|2’ где D^k – дисперсия шума. В силу некоррелированности сигнала и шума на входе корректора их дисперсии складываются:

^=X-Xf+Md*r =

= Ос^-укСкХ1-/кС*>ОшкСкС*к =

= D_ck (1 - y_kC_k - y*_kC‘_k + y_ky_kC_kC‘_k У D_mkC_kC*_k.

Для минимизации этой суммы найдем опти- мальные значения Ck * Обозначим Ckc и X

– вещественную и мнимую компоненты Cr , соответственно:

Рд = D_ck [1 — у_kcC_kc + y_ksC_h — у _к,С к + у^C_ts + + Ук + YL УХ + X)]+ П_шк Ук + Су).

Найдем частные производные и приравняем их к нулю:

ЭРЕк

ЭСкс

-ОсУ-2укс+у2кс-2Скс+Ук5-2СУ

+ Dmk.2Ckc=0,

= Dck {2уь +укс • 2Cks + уks • 2СЬ)

с^/Х.+гуХк xhlx +2ylDck

шА ^ks ^и?

+ ^D_mk ] - D_ck 2у_кс, + 2П_ш4]=-^2/^.

Таким образом, оптимальный комплексный коэффициент передачи корректора для k -ой частотной компоненты равен

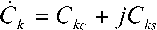
рск-ук

Vk\²D_ck +Р_шк

Интересно отметить, что при отсутствии шума Хшк = 0) рассмотренный корректор вырождается в корректор по алгоритму сведения к нулю:

р_ск-у; _ 1

ЫХ 7

Частные случаи для (2): при y_k^Q C_k^Q- при У к -^ ⁰⁰ С к ^ 0. Формула (2) может быть переписана в виде:

G =G, с            (4)

vk ^kl vk2’               v '

где

с = ^1^1

D=k\yk\ +Ршк

Таким образом, частотный корректор с коэффициентом передачи ^к ^? используемый для выравнивания сигнала в программном комплексе, можно представить в виде каскадного включения двух частотных корректоров с коэффициентами передачи Qi ^и Q-2 (см. рис. 9).

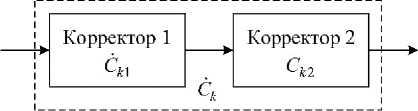
Рис. 9. Схема частотного корректора

Символы на выходе первого корректора c_k i содержат переданную информацию, искаженную только аддитивным белым гауссовским шумом (АБГШ) в канале. Главным недостатком корректора с нулевыми взаимными помехами является бесконечное увеличение АБГШ в «нулях» частотной характеристики канала. Но его достоинством является выравнивание сигнала при неизвестном D^k •

Корректор С к 2. организован по принципу фильтра Колмогорова-Винера [1], который является оптимальным фильтром формирования выходного сигнала при известной спектральной плотно сти полезного сигнала D_ck и шума . В каче стве критерия его оптимизации используется среднеквадратическое отклонение выходного сигнала от передаваемого.

На рис. 10-12 показаны три варианта частотной характеристики двухлучевого канала, передаточной функции корректора, рассчитанной по (2), и спектральной плотно сти шума на выходе корректора. В первом варианте (обозначенном цифрой «1») соотношение лучей 1:0,4; во втором варианте «2» – 1:0,65; в третьем «3» – 1:1. Рассмотренный способ коррекции сигнала предполагает знание импульсной характеристики канала. Способы получения этой информации описаны, например, в [7-8]. Полученный от использования такого частотного корректора эффект – уменьшение искажений, внесенных многолучевостью, и возможно сть корректора выравнивать сигнал, прошедший через канал с любой ИХ.

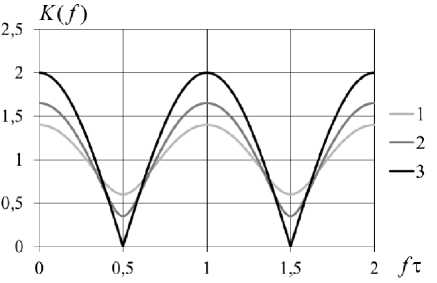
Рис. 10. Частотная характеристика двухлучевого канала

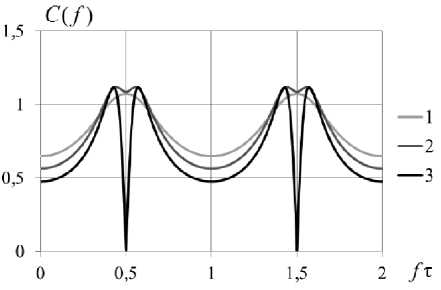
Рис. 11. Передаточная функция корректора

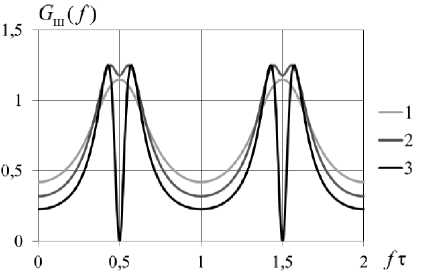
Рис. 12. Спектральная плотность шума на выходе корректора

Результаты статистического имитационного моделирования

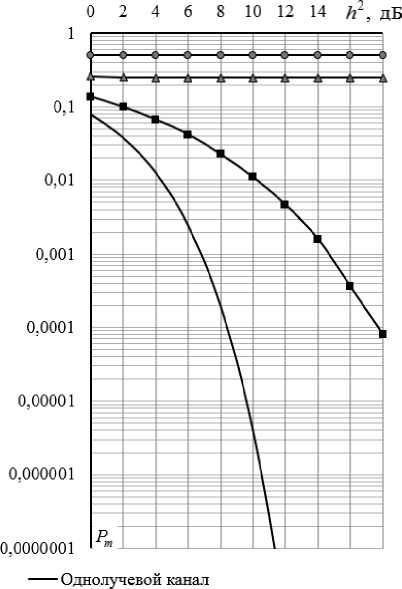
Многочисленные опыты показали, что результаты работы алгоритмов с циклическим префиксом и с пост-паузой одинаковы, поэтому далее приведены результаты моделирования только для метода циклического префикса. На рис. 13 приведены графики зависимостей вероятности ошибки для сигнала ФМ-2 в условиях передачи информации по однолучевому каналу, по двухлучевым каналам без корректора, с корректором по минимуму СКО и корректором по алгоритму сведения к нулю с соотношением лучей в канале 1:1.

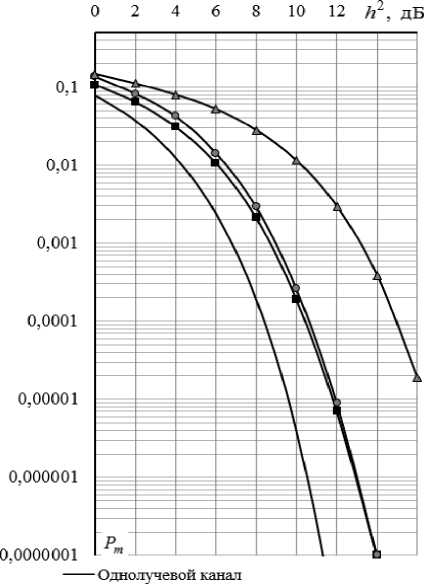
На рис. 14 приведены эти же графики для соотношения лучей 1:0,5 (или 0,5:1).

На рис. 13-14 значения вероятности ошибки для сигнала, передаваемого в однолучевом канале, рассчитаны по формуле [1]:

Р_т = ^Nn\         (5)

где Q(x) - ^-функция:

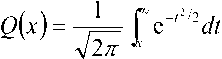
^т – отношение энергии сигнала, несущего этот символ, к спектральной плотности мощности БГШ. Для сигнала, передаваемого в двухлучевом канале, вероятность ошибки получена экспериментальным путем.

-■—Двухлучевой канал с корректором по минимуму СКО

—°—Двухлучевой канал с нуль-форсирующим корректором

—л—Двухлучевой канал без корректора

Рис. 13. Графики зависимостей вероятности ошибки от ОСШ на символ в канале с соотношением лучей 1:1

Выводы

Использование методов пост-паузы и циклического префикса полностью решает проблему возникновения «краевых эффектов» при преобразовании Фурье. Если нет помех, то коррекция сигнала может быть осуществлена как угодно точно.

При слабо выраженной многолучевости результаты работы корректоров по алгоритмам сведения к нулю и минимуму СКО отличаются незначительно. Напротив, при наличии в канале двух лучей одинаковой интенсивности нуль-фор-сирующий корректор только ухудшает работу приемника, выдавая несократимую вероятность ошибки. Выравнивание сигнала в частотной области (FDE) с применением БПФ обеспечивает высокую точность корректирования принимае- мого сигнала (по сравнению с выравниванием во временно области), а также высокую скорость обработки сигнала (по сравнению с переборными алгоритмами).

—■—Двухлучевой канал с корректором по минимуму СКО

—°—Двухлучевой канал с нуль-форсирующим корректором

—^—Двухлучевой канал без корректора

Рис. 14. Графики зависимостей вероятности ошибки от ОСШ на символ в канале с соотношением лучей 1:0,5 (или 0,5:1)

При слабо выраженной многолучевости результаты работы корректоров по алгоритмам сведения к нулю и минимуму СКО отличаются незначительно. Напротив, при наличии в канале двух лучей одинаковой интенсивности нуль-форсирующий корректор только ухудшает работу приемника, выдавая несократимую вероятность ошибки. Выравнивание сигнала в частотной области (FDE) с применением БПФ обеспечивает высокую точность корректирования принимаемого сигнала (по сравнению с выравниванием во временной области), а также высокую скорость обработки сигнала (по сравнению с переборными алгоритмами).