Программный комплекс расчета давления в смазочном слое подшипника скольжения
Автор: Иванов В.А.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Технологические процессы и материалы
Статья в выпуске: 3 т.19, 2018 года.
Бесплатный доступ
Описан итерационный алгоритм схемы расчета распределения давления в смазочном слое подшипника скольжения конечной длины, которая учитывает переменную вязкость, зависящую от давления и температу- ры, эффекты кавитации и упругой деформации контактирующих тел в зоне повышенного давления, а также неровности поверхностей и условия неполного прилипания жидкой смазки на рабочих поверхностях тел. Центральной частью алгоритма является блок численного решения модернизированного уравнения Рейнольдса относительно давления на основе неявной конечно-разностной схемы с расщеплением по направлениям. На каждом шаге итерации по найденному распределению давления вычисляется распределение мощности тепло- выделения в слое, с использованием которой выполняется расчет распределения температуры в слое смазки путем решения уравнения теплопроводности методом разложении Фурье. Вычисленные значения давления и температуры используются при перерасчете коэффициента вязкости на каждом шаге итераций. Показана достаточно быстрая сходимость итерационных циклов. Проведены сравнительные тестовые расчеты с ря- дом других программ, которые показывают хорошую сходимость и высокую точность вычислений. Представ- ленный метод решения задачи упруго-гидродинамического контакта реализован в виде комплекса программ, вычислительная часть которого написана на языке программирования Fortran 77. Интерфейс разработан на платформе Microsoft.NET Framework с использованием языка С# (C Sharp) для операционных систем Windows 7/8/10. Программный комплекс позволяет эффективно и быстро выполнять расчет механических и термоди- намических характеристик смазочного слоя при высоких нагрузках, не требуя больших вычислительных ресур- сов. Это обстоятельство имеет важное значение при проектировании узлов трения при создании космических аппаратов и пусковых установок. Применение данного программного комплекса позволяет существенно уско- рить расчеты конкретных инженерных задач, снизить требования к используемой компьютерной технике и снизить затраты на вычислительные ресурсы.
Смазочный слой, гидродинамическая смазка, программный комплекс
Короткий адрес: https://sciup.org/148321868
IDR: 148321868 | УДК: 628.822 | DOI: 10.31772/2587-6066-2018-19-3-540-549
Текст научной статьи Программный комплекс расчета давления в смазочном слое подшипника скольжения
Введение. Гидродинамическая теория смазки широко применяется для расчета и конструирования подшипников скольжения с жидкой смазкой, которые являются важными конструктивными элементами разнообразных механизмов и машин. Существует большое количество публикаций, посвященных этой теме, например [1–4]. Роль упругих деформаций становится очень важной для тяжело нагруженных цилиндрических подшипников скольжения. Поэтому возникла необходимость учета упругих деформаций рабочих поверхностей в гидродинамической теории смазки. Это привело к развитию так называемой упруго-гидродинамической теории, в которой согласованно рассматривались течение смазочного слоя и деформация поверхности контакта, вызванная повышенным давлением в смазочном слое [5]. В этой теории важное место отводится проблеме определения связи между распределением давления в слое и деформацией поверхности.
Основными элементами конструкции гидродинамического подшипника скольжения являются цилиндрический вал, смазочный слой, вкладыш и корпус. Обычно вкладыш подшипника изготавливается из более податливого материала по сравнению с корпусом, который имеет высокую твердость и мало деформируется. По этой причине деформациями корпуса часто пренебрегают и учитывают только деформации вкладыша [6]. При таком упрощенном подходе деформации тонкого вкладыша, ограниченные жестким корпусом, определяются малым параметром – отношением толщины вкладыша к радиусу кривизны. Как показано в монографии [6], в первом приближении по этому малому параметру деформации вкладыша пропорциональны локальному значению давления. Коэффициент пропорциональности называют податливостью вкладыша. Данное приближение связано с известной гипотезой Винклера. В случае цилиндрической геометрии точное значение коэффициента податливости может быть найдено из аналитического решения [7]. В общем случае необходимо учитывать не только деформации вкладыша, но также и деформации корпуса, имеющего конечную жесткость.
В настоящее время широкое применение получили различные мультидисциплинарные комплексы, позволяющие моделировать различные условия работы узлов трения в очень широком диапазоне условий и нагрузок, однако, чем больше реальных факторов учитывает программный комплекс, тем больше требуется временных и вычислительных ресурсов на моделирование и расчет конкретного узла. А если же узел работает в нестационарном режиме, то временные затраты возрастают многократно. В этом ключе рассмотрим предлагаемый программный комплекс расчета давления в смазочном слое подшипника скольжения, основанного на решении модернизированного уравнения Рейнольдса с учетом проскальзывания на границах тел и жидкости, а также с учетом переменной вязкости смазочного слоя.
Для описания предлагаемого программного комплекса рассмотрим цилиндрический подшипник скольжения, в котором смазочный слой разделяет стальной вал и бронзовый вкладыш, граничащий со стальным корпусом, как показано на рис. 1.
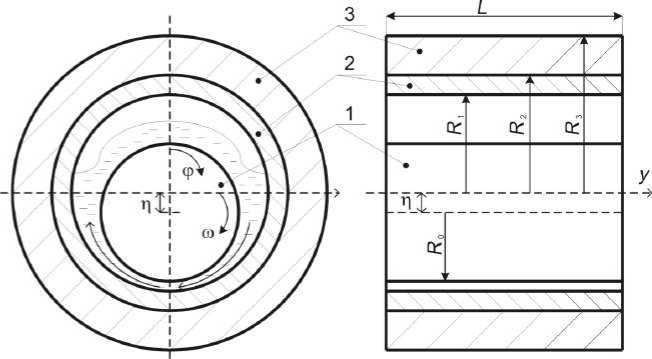
Рис. 1. Геометрическая схема подшипника скольжения: 1 – вал; 2 – бронзовый вкладыш; 3 – корпус
-
Fig. 1. Geometric diagram of a plain bearing:
1 – shaft; 2 – bronze liner; 3 – case
На рис. 1 ω – угловая скорость вращения вала, φ – азимутальный угол, отсчитываемый в направлении часовой стрелки от точки максимального зазора, η и R 0 – эксцентриситет и радиус цилиндрического вала, R 1 – внутренний радиус вкладыша, R 2 и R 3 – внутренний и внешний радиусы цилиндрического корпуса, L – длина подшипника. В расчетах используем нулевые граничные условия для деформаций на заданной внешней границе корпуса подшипника. Между валом и вкладышем располагается тонкий слой жидкой смазки, называемый смазочным слоем. Также ставим нулевые граничные условия для давления на торцах подшипника.
Расчет давления. Распределение давления P в смазочном слое определяется из модернизированного уравнения Рейнольдса [8]
div [ 5 ( h ) v p ] = 2 v ( V r ( h ) ) +d h, (1)
где h – толщина жидкого слоя; V – сумма скоростей тел в точке контакта:
V = V 1 + V 2.
где а - пьезокоэффициент, характеризующий изменение вязкости в зависимости от давления; ц о - динамическая вязкость при P = 0; Ω 0 – так называемый коэффициент крутизны вискограммы.
Тепловой расчет. Расчет мощности тепловыделения Q для подшипника скольжения, работающего в гидродинамическом режиме, определяется следующим выражением:
Q = —
12 ц
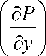
1 ( d P ]
+ т1 I
R 12 (дф)
+ ц V 2. (6)
h
Запишем уравнение теплопроводности в цилинд- рических координатах:
1 a f а т)
I r—1 + r д r ( д r )
1 д 2 T r 2 дф 2
Решение уравнения (7) можно представить в виде разложения Фурье:
го т = а о +Z[ ak cos(kф)+bk sin(kФ)]+T>, (8)
k = 1
При этом толщина жидкого слоя h учитывает как геометрический зазор между контактирующими телами h g , так и деформацию упругой поверхности 5 , вызванную избыточным давлением в слое:
где ak и bk – коэффициенты Фурье.
На внутренней границе при r = R 1 имеем граничное условие для потока тепла из смазочного слоя:
2п h = 1 + n cos(ф) + j P (ф')K(ф-ф'^Ф,
P > 0;
V V h = 0, P < 0,
где K (φ – φ') – функция податливости, не зависящая от распределения давления в слое, но зависящая от геометрических и упругих свойств контактирующих материалов [9].
Заметим, что уравнение (2) учитывает эффект кавитации (вспенивания) для отрицательного давления.
При отсутствии проскальзывания между контактирующими телами функции S ( h ) и Γ( h ) в уравнении (1) имеют вид
5 = , Г ( h ) = h . (3)
12 ц
При частичном или полном проскальзывании между контактирующими телами функции S ( h ) и Γ( h ) принимают следующий вид:
h 2 [ h ( 4 k 1 + 4 k 2 + h ) + 12 k 1 k 2 ] 12 ц ( k 1 + k 2 + h )
Г ( h ) =
h ( h + 2 k , ) k 1 + k 2 + h
Важно отметить, что вязкость смазочного слоя ц сильно зависит от таких факторов, как температура T и давление P . Существует множество эмпирических моделей изменения вязкости жидкого слоя, однако наиболее точной из них является формула Петрусеви-ча, которая описывает зависимость вязкости от температуры и давления:
ц ( P , T ) =цоехр(а P -П о T ), (5)
„ d т
Q = -х^ , 5 r
где Q – мощность тепловыделения в смазочном слое, определяемая формулой (6).
Функцию мощности тепловыделения также разлагаем по Фурье-гармоникам:
1 2 1
® k =- f Q (ф)cos( k ф) d ф , п о
1 2 п
1 2 1
На внешней границе задаем температуру окружающей среды T 0 :
T ( R з ) = T о .
Применяя разложение Фурье к формуле (9), получаем уравнения для коэффициентов разложения:
д ак х —- = © k д r
д Ьк .
х —k = © k , д r
где коэффициенты ak , bk удовлетворяют дифференциальным уравнениям
1 д Г д ак ) k2 _
--1 r—k" I— aa= = о :
r d r ( d r J r2
1 д Г д ьк ) k2, .
--1 r —- I ьЬ= = о r d r ( d r J r2
1 Af r | = о r d r ( d r J
Решая уравнения (12), определим коэффициенты a k и b k .
Программный комплекс расчета давления в смазочном слое. Данный программный комплекс создан на основе итерационный схемы, которая включает циклический пошаговый расчет всех необходимых параметров, описанных ниже. Данный комплекс позволяет вычислять распределения давление в смазочном слое подшипника скольжения конечной длины, при этом комплексно учитывать такие важные факторы, как деформация поверхностей под действием избыточного давления, шероховатость границ, частичное проскальзывание, переменная вязкость, зависящая от температуры и давления, скорость сближения границ и кавитация.
Алгоритм расчета давления реализован в виде конечно-разностной схемы:
RR a o = — ln—.
X R 1
Множители 0 kj и 0 * kj представляют собой коэффициенты Фурье разложения мощности тепловыделения Q , зависящей от градиентов давления:
1 nx
0 k , j =- £ Qi, j cos( kx i) A x , n i = 1
nx
0 k j = - £ Qi j sin( kx i )A x , 1 < k < NF , n i = 1
О . =S. .
Qi , j i , j
3 i , j
~
Ц i , j
P, ■ i + 1, j
-P,.
i - 1, j
vv
2 A x
+
Pi , j + 1 Pi , j - 1 J
v
2A y
J
+--
H i , j
1 Ге p n 112 le । e ip'+1/2 । e p n +1/2l_i_
Аф 2 L S i + 1/2, — P + 1, — 1 ' — + S ' — ) P ■ — + S - 1/ 2 , P " j ] +
? _ 4цоR2to2 Si,j = d di,j
S i,j n n n
+ A y 2 ( i • j + 1 i ■ j i • j - 1 )
p ” p ” P ” +1/ 2
-i ^ i - 1 +a -j1—
2Aф
A t
n i,j
S i , j
ru
S— 8P” + 1 A y2 (6 PiJ + i
6 Pn+1 = a ——
2 6 P " + 1 +6 P n ,+V) = i , j i , j - • /
/ p n + 1/2 ( P i , j
A /
P” +1 = P ” .+5P ” +1, i , j i , j i , j ,
P i , n j )
= H — H — 4 ki + 4 к 2 + H — ) + 12 kk 2 ]
Ц ( k i + k 2 + H i j )
= H^HM + 2 k i )
k i + k 2 + H i , j
i = 1... nx, j = 1... ny,
H j = 1 -n cos ( ф , ) + dt j , P > 0;
n
H i + 1, j
- H" = 0, P < 0;
, j
Nx
d , j = A o £ P k K ( ф - -ф к ) АФ, к = 1
A 0 = 6 K 0 ц 0 R 2 ® / d 3 .
На основе распределения давления на каждом итерационном шаге выполняется расчет температуры T методом Фурье:
NF
T , j = a o, j ' Х ( а. , j cos ( kX ) + b k , j sin ( kx - ))+ T o , (14> к = 1
где коэффициенты разложения a k , b k вычисляются по формулам
a k , , =® k , 7 ~ k , b k , , =® k , j a k , (15)
~ ak
R 3 k
f Ri
/
X
v
X k -1
R1J +
R зJ
/
v
x k+1 R3 ) RJ
R 3
k
R3 J v R1 J
Для определения текущего прогиба поверхностей, зависящего от распределения давления, используется аналитическая аппроксимация функции податливости, учитывающая геометрические и механические свойства контактирующих поверхностей:
K ( x ) = 1,2
( R 2 - R 1 ) (1 + m ,)(1-2 m ,) + E 1 1 - m 1
+ ( R з - R 2 ) (1 + m 2 ) ( 1 -2 m 2 ) -[
E 2
1 - m 2
L1 + Y x1
-p л7
,
где параметры α', β, γ – служат для корректировки аналитической функции податливости; m – коэффициент Пуассона; E – модуль упругости.
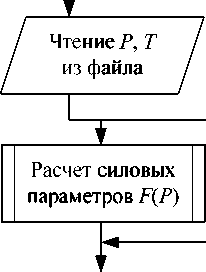
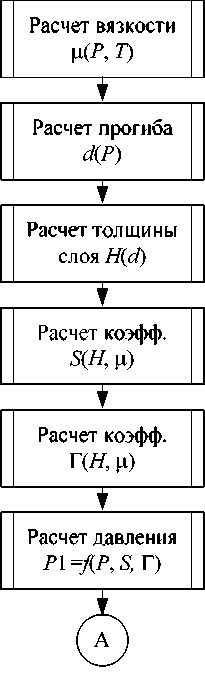
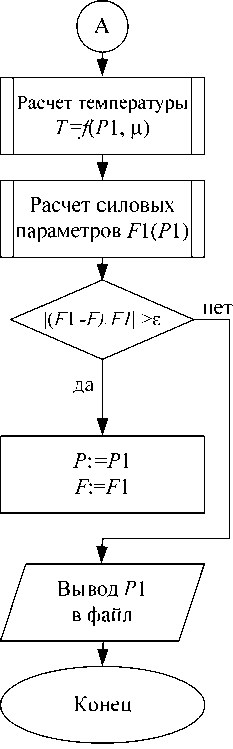
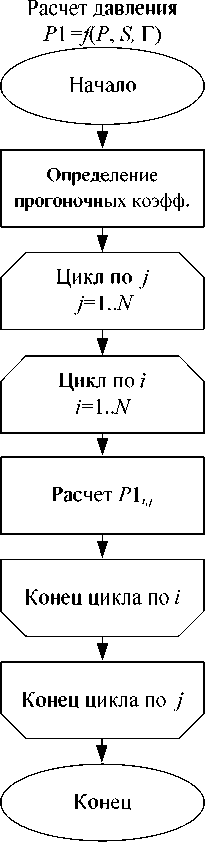
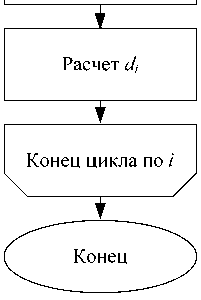
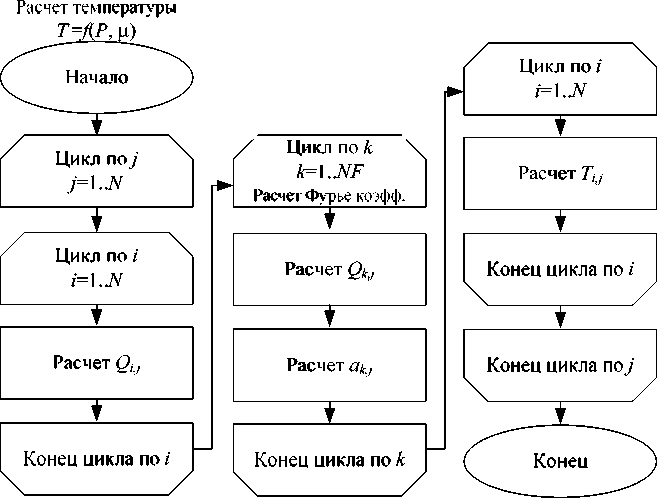
Блок-схемы программного комплекса и вспомогательных подпрограмм представлены на рис. 2 и 3. Для расчета требуется задать параметры расчетной сетки, геометрические и механические параметры контактирующих тел, динамические характеристики вала, вязкостно-температурные параметры масла и выбрать начальное распределение давления P , которое задано по умолчанию либо задается вводом массива значений из файла.
Далее выполняется переход к основному итерационному циклу программы. Внутри итерационного цикла выполняется расчет давления P по неявной схеме методом переменных направлений с использованием скалярных прогонок. На основе нового распределения давления выполняется перерасчет температуры (подпрограмма Т ( P 1)), вязкости (подпрограмма ц ( P , T) ) и прогиба (подпрограмма d ( P )). Толщина смазочного слоя определена с помощью функции H ( d ). Функции S ( H , ц ) и Г( H , ц ) дают возможность учитывать как полное прилипание ( k 1,2 = 0), так и частичное проскальзывание (0 < k 1,2 < 1) смазочного материала на поверхностях.
Затем выполняется расчет основных силовых показателей, таких как азимутальная и осевая компоненты несущей способности Wx и Wy , полная несущая способность Wtot , число Зоммерфельда Zommer , момент трения M tr . После каждого итерационного шага проверяется критерий сходимости итераций. Итерации прекращаются при достижении достаточно мало-
го относительного изменения W tot на итерационном шаге:
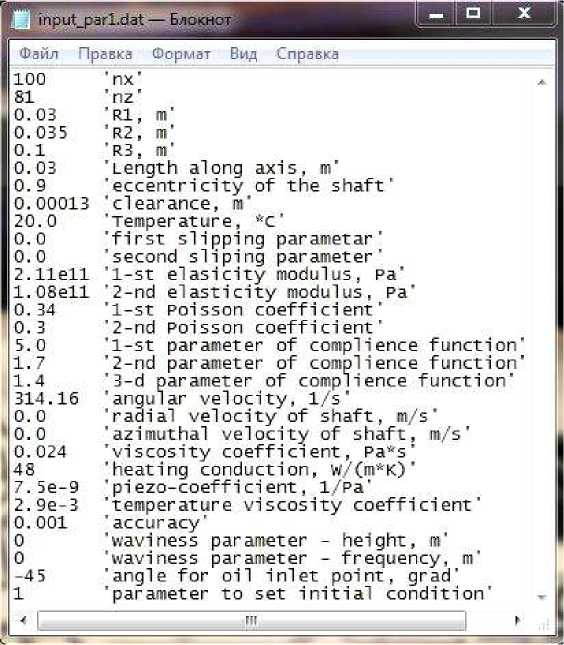
| (w - wo-) / w\ По завершении всего итерационного цикла все рассчитанные параметры сохраняются в файлы. Интерфейс программы состоит из рабочего окна, в котором располагаются четыре кнопки: Parameters, Run, Results и Exit. Интерфейс программы представлен на рис. 4. Кнопка Parameters открывает файл входных параметров (рис. 5). Задание P, T по умолчанию Рис. 2. Блок-схема программного комплекса Fig. 2. Block diagram of the software package Расчет прогиба Цикл по z i=\..N Рис. 3. Блок-схема вспомогательных подпрограмм Fig. 3. Block diagram of subprograms Рис. 4. Интерфейс программы Fig. 4. The interface of the program В этом файле задаются параметры расчетной сетки (число точек по азимуту nx и вдоль оси ny), геометрические параметры, смещение оси вала (eccentricity), температура внешней среды (temperature), два граничных параметра проскальзывания, модули упругости и коэффициенты Пуассона деформируемых тел, три параметра функции податливости, угловая скорость вращения вала, радиальная и азимутальная скорости смещения оси вала, динамический коэффициент вязкости, коэффициент теплопроводности мате- риала, коэффициенты, характеризующие зависимость вязкости от давления (piezo-coefficient) и температуры (temperature viscosity coefficient), параметр допустимой погрешности (accuracy), параметры мелкомасштабной волнистости поверхности (waviness parameter), азимутальный угол, определяющий место подачи масла, и целочисленный параметр выбора начального распределения давления («0» – задается постоянное начальное давление внутри программы, «1» – считывается массив давления из файла). Запуск программы инициируется кнопкой Run. Через определенное число шагов итерации значения силовых показателей выводятся на экран. Выдаваемое программой изображение на экране представлено на рис. 6. График сходимости итераций для двух значений эксцентриситета xlam представлен на рис. 7. Рис. 7 показывает, что даже при больших значениях эксцентриситета итерации сходятся довольно быстро, за 200 шагов. Результаты расчета записываются в четыре текстовых файла, показанных на рис. 8, которые выводятся на экран после нажатия кнопки Results. Рис. 5. Исходные данные Fig. 9. Pressure in the lubricating layer of the bearing: 1 – equation (1) taking into account the cavitation effect; 2 – equations (1) without taking into account the cavitation effect; 3 – Simulation in Cosmol Multiphysics Вычислительная часть программного комплекса написана на языке программирования Fortran 77. Интерфейс разработан на платформе Microsoft .NET Framework с использованием языка С# (C Sharp) [10] для операционных систем Windows 7/8/10. Данный программный комплекс зарегистрирован Федеральной службой по интеллектуальной собственности [11]. Тестовые расчеты. Для тестирования данного программного комплекса проведены сравнения с опубликованными результатами других авторов для подшипника скольжения. Первое сравнение проведено с программным пакетом, основанным на методе конечных элементов и широко применяемым для расчета различных задач гидродинамики. Подробное изложение построения модели в пакете Сomsol Multiphysics описано в работе [12]. Расчет выполнялся для следующих параметров: L = 0,125 м, R1 = 0,25 м, µ = 0,19 Па∙с, относительный эксцентриситет ηɶ = 0,5, скорость вращения вала 1000 об/мин. На рис. 9 представлены графики давления в смазочном слое, вычисленного с помощью описанного выше комплекса и пакета Сomsol. Рис. 9 показывает, что при расчете давления в смазочном слое в пакете Сomsol Multiphysics не учтен кавитационный эффект. Вследствие этого возникает область отрицательного давления (кривая 3), что приводит к снижению максимума давления на 17 % по сравнению с расчетом, выполненным на основе опи- санного выше программного комплекса, учитывающего кавитационный эффект и исключающего отрицательные давления (кривая 1). В то же время, решение, полученное с помощью данного комплекса при отключенном блоке кавитации (кривая 2), довольно близко совпадает с решением, полученным в программном пакете Сomsol. В этом случае различие значений максимальных давлений в слое составляет 6 %. Кроме того, проводилось сравнение с расчетами, представленными в работах [13; 14]. В этих работах изложено численное моделирование гидродинамических подшипников скольжения на основе решения классического уравнения Рейнольдса методом Патанкара [15] при постоянной вязкости, фиксированной температуре и отсутствии деформаций поверхностей. Для сравнения выбран важный параметр Зоммер-фельда Z, который обратно пропорционально зависит от безразмерной несущей способности W': Z= 3πW′ W′ =∫∫Pɶcosϕdϕdyɶ . На основе описанного выше программного комплекса получено значение параметра Зоммерфельда 0,123, которое менее чем на 1 % отличается от аналогичного значения, вычисленного в работах [13; 14], S = 0,121. Описанные сравнения расчетов давления в смазочном слое обосновывают работоспособность предложенного выше вычислительного алгоритма и программного комплекса, позволяющего эффективно выполнять расчеты распределения давления в зоне упруго-гидродинамического контакта тел с хорошей точностью. Заключение. Создан программный комплекс расчета давления в смазочном слое подшипника скольжения с учетом деформации и волнистости контактирующих поверхностей, эффекта кавитации, проскальзывания на границах тел и жидкости, а также переменной вязкости смазочного слоя, зависящей от термодинамических параметров. Данный программный комплекс может применяться для расчета как стационарной работы подшипника, так и для нестационарного режима, возникающего в результате колебания внешней нагрузки.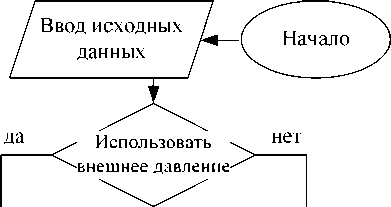

Список литературы Программный комплекс расчета давления в смазочном слое подшипника скольжения
- Williams J. A. Engineering tribology. N. Y.: Oxford University Press Inc., 1994. 242 p.
- Hamrock B. J., Schmid S. R., Jacobson B. O. Fundamentals of fluid film lubrication. N. Y.: Marcel Dekker, Inc., 2004. 703 p.
- Bair S. High-Pressure Rheology for quantitative elastohydrodynamics // In Tribology and Interface Engineering Series. Elsevier. 2007. 54 p.
- Szeri A. Z. Fluid film lubrication. Cambridge: Cambridge University Press, 2011. 273 p.
- Lugt P. M., Morales-Espejel G. T. A Review of elasto-hydrodynamic lubrication theory // Tribology Transactions. 2011. Vol. 54. P. 470-496.


