Программный уровень общего управления агроценозом с учетом влияния сорной растительности на состояние посева культуры

В современном растениеводстве давно сложилась традиционная парадигма раздельного управления состоянием посевов и сорных растений в составе одного агроценоза. Развитие точного земледелия (ТЗ) послужило стимулом для создания эффективной теории управления агротехнологиями. Но в большей степени это отразилось в задачах управления состоянием посевов сельскохозяйственных культур. Здесь уже разработаны многие поло- жения современной теории, начиная с создания общей концепции управления и заканчивая алгоритмами управления на различных временных уровнях (1, 2). Согласно этой теории, становится возможным формировать программы управления, представляющие собой последовательности технологических операций с оптимальным уровнем доз вносимых удобрений и норм поливов. Что касается управления состоянием сорной растительности, то здесь успехи в разработке теории более скромны, и на сегодняшний день оптимальные дозы обработок посевов гербицидами еще научно не обоснованы. При этом существующая теоретическая база управления состоянием сельскохозяйственных культур не учитывает того, что в составе агроценоза присутствует сорная растительность, и внесение удобрений и поливы стимулируют ее рост и развитие наряду с возделываемой культурой. Одновременно обработки агроценоза гербицидами подавляют рост не только сорной растительности, но и основной культуры. В итоге такое раздельное управление приводит к существенным потерям урожая, перерасходу удобрений и гербицидов и ухудшению экологических показателей окружающей среды. Появление в последнее время достаточного числа публикаций по совместному внесению удобрений и гербицидов показывает, что технологическая наука стремится к устранению недостатков существующей парадигмы раздельного управления (3-5). Это ставит новые задачи перед наукой об управлении агротехнологиями, заставляя ее рассматривать поле с агроценозом, как единый объект управления (ОУ).

Согласно предложенной концепции управления агротехнологиями в ТЗ, общая задача управления включает в себя четыре уровня задач, решаемых в разные масштабы времени (1). На верхнем 1-м уровне решается задача управления севооборотами в годовом масштабе; на 2-м уровне, реализуемом в суточном масштабе на одном интервале вегетации, решается задача программного управления. Первые два уровня являются планирующими и решаются предварительно, вне реального времени. Задачи 3-го и 4-го уровней, где непосредственно формируются технологические операции, реализуются в реальном времени. Из всех приведенных уровней программный уровень управления является ключевым, так как именно через него осуществляется связь стратегических задач управления с задачами реального времени. На программном уровне управления планируется оптимальная последовательность технологических операций, обеспечивающая достижение требуемого результата (2).

В соответствии с предложенной концепцией управления на программном уровне в качестве ОУ принимается поле с посевом сельскохозяйственной культуры. Однако в концепции не учитывается тот факт, что на этом же поле в составе агроценоза, кроме основной культуры, произрастают однолетние и многолетние сорные растения. Они конкурируют с растениями возделываемой культуры за влагу и элементы питания, а потери урожая от засоренности посевов могут превышать 50 %. Следовательно, оптимальные технологические программы операций на рассматриваемом интервале вегетации должны включать в себя не только операции по внесению удобрений и поливы, но и обработки гербицидами. При этом такие программы должны формироваться с учетом того, что минеральное питание стимулирует рост как культурных растений, так и сорняков, а гербициды не только подавляют рост и развитие сорняков, но действуют угнетающе и на куль- турные растения.

Формирование единой согласованной по состоянию растений основной культуры и сорных растений программы одновременного внесения минеральных удобрений и обработок гербицидами позволит избежать потерь урожая и перерасходов минеральных удобрений и гербицидов. Кроме того, оптимизация доз удобрений, отвечающих биологическим потребностям культуры в питательных элементах, активирует процессы обмена веществ, обеспечивает ускорение инактивации поступающего гербицида и повышает устойчивость к нему у защищаемого растения. При этом защищаемая культура вследствие более интенсивного накопления органической массы получает значительно меньшую дозу гербицида на единицу массы, то есть происходит ростовое уменьшение содержания гербицида в тканях, а меньшие количества препарата при оптимальном обмене веществ быстрее инактивируются. Оптимальные условия питания также повышают общую биологическую конкурентоспособность культуры по отношению к сорнякам (3-5).

Анализ зарубежных публикаций в области управления агротехнологиями показал, что на сегодня разработаны только частные аспекты и мало связанные между собой задачи управления состоянием посевов культур: модели оценивания и предсказания биомассы посевов (7, 9), принципы зонального управления азотным питанием и рисками (10-12, 18), общие принципы управления ресурсами сельскохозяйственного производства, включая ресурсные модели (13-17, 19). На основании такого анализа можно утверждать, что до настоящего времени еще не разработана единая теоретическая база управления агротехнологиями в ТЗ.

Это обусловлено недостаточной изученностью агроценоза как единого объекта управления, для которого еще не созданы комплексные модели взаимосвязи состояния культур и сорных растений в посеве. В большой обзорной работе (20) обсуждается природа и практика применения полного ряда имитационных моделей по экологии, биологии и борьбе с сорными растениями, а также использование таких моделей для получения информации и поддержки принятия решений. Как правило, специалисты по защите растений исходят из количественной оценки плотности популяции и агрессивности сорняков. Важное место занимают модели, прогнозирующие потери урожая и устанавливающие пороговые значения для определения методов и сроков мероприятий по борьбе с сорной растительностью (21, 22). Были реализованы несколько подходов, основанных на связи между плотностью сорняков в посеве и потерей урожая, и доказано, что эта зависимость описывается прямоугольной гиперболой (23).

Биомасса сорняков может быть надежным предиктором потери урожая (24, 25): чем она выше (независимо от плотности сорняков в агроценозе), тем больше снижается урожайность культуры. Однако учет биомассы сорных растений требует много времени, и этот показатель трудно контролировать в полевых условиях. Еще одна проблема при прогнозировании потерь урожая по биомассе сорняков заключается в том, что нет четкого понимания, какую часть этой биомассы следует рассматривать. Пример по прогнозированию воздействия сорняков и потерь урожая — предложенная M.J. Krop и J.T. Spitters (26) модель для сахарной свеклы.

Адаптивные изменения сорняков — возможно, еще один фактор, который требуется учитывать при анализе системы сорняки—сельскохозяй- ственные культуры. При повышении конкурентоспособности сорных растений снизится потенциал сельскохозяйственных культур. Как следствие, точность прогнозных моделей потери урожая из-за сорняков постепенно будет снижаться (27, 28). Поэтому для корректного учета взаимного влияния сорняков и сельскохозяйственных культур необходима периодическая параметризация и повторная калибровка моделей.

На практике решение проблемы потерь урожая от сорняков требует знаний о видоспецифичных, изменяющихся во времени отношениях между сорными и культурными видами растений, понимания краткосрочных и долгосрочных последствий принятой тактики защитных мероприятий (29, 30). Без подобным образом интерпретируемой информации о многофакторных событиях нельзя разработать программы защитных мероприятий, которые будут эффективны, функциональны и не повредят нецелевым организмам (31-34).

Особенно велика потребность в средствах поддержки принятия решений (СППР) для специалистов-практиков. В таких СППР должны сочетаться модели динамики популяции сорняков, экономической эффективности технологии (35-37) и ее воздействия на окружающую среду (36, 37). Такие СППР позволят практикам моделировать новые варианты управления в местных условиях, адаптировать концепции устойчивого управления с учетом особенностей резидентных сорняков (38-40) и сравнивать вероятные краткосрочные результаты возможных вмешательств. Некоторые СППР моделируют краткосрочные результаты тактики механического контроля (31, 41-43). Наиболее эффективны тактики СППР для решений по химической борьбе с сорными растениями (36, 37, 42, 44, 45). Эти СППР предоставляют руководство для выбора по ряду аспектов применения гербицидов (31, 38, 46-49). Кроме того, многие программные решения предлагают прогнозы финансовых последствий возможных мероприятий (31, 42, 46-49).

Инструменты поддержки принятия решений для превентивного управления выполняют две основные задачи: во-первых, они предсказывают засоренность посевов и прибыли при разных вариантах вмешательств в течение несколько лет; во-вторых, они предоставляют эти прогнозы в рамках соответствующей намеченной цели (40-44).

Проведенный анализ показывает, что при всей широте охвата проблемы в предлагаемых разработках не представлена такая постановка задачи управления агроценозом, которая включала бы как обоснованные математические модели, так и выбор достижимых целей управления, форм критериев оптимальности и эффективных алгоритмов управления, посредством которых формируются программы технологических операций, обеспечивающих достижение поставленных целей управления.

В предлагаемой работе нами впервые ставится и решается задача единого управления агроценозом на программном уровне, реализуемом на одном периоде вегетации. Для ее решения в ранее разработанной теории управления агротехнологиями видоизменены математические модели состояния посевов возделываемой культуры, в которых отражено влияние гербицидов. Кроме того, в состав задачи управления введена модель параметров состояния доминирующих видов сорных растений, в которых, кроме доз обработок гербицидами, отражено влияние доз обработок минеральными удоб- рениями. При этом нами предложена новая трехэтапная процедура программного управления агроценозом. На первом этапе формируется программа изменения параметров почвенной среды, обеспечивающая достижение требуемой урожайности культуры. На этом этапе влияние обработок гербицидами на состояние посева культуры не учитывается. На втором этапе находится последовательность технологических операций, обеспечивающая наилучшее приближение параметров почвы к оптимальной программе, полученной на первом этапе. Наконец, на третьем этапе находят оптимальную последовательность обработок гербицидами, выполняемых одновременно с другими технологическим операциями.

Цель настоящей работы заключалась в дальнейшем развитии теории программного управления агротехнологией за счет перехода к объекту управления, которым служит поле с агроценозом, где основной культурой является яровая пшеница.

Методика . Для решения задачи применяется классическая теория управления с использованием методов динамического программирования и принципа максимума Понтрягина (6). Согласно этой теории, исходный пункт решения любой задачи программного управления — выбор достижимой цели. Когда мы имеем дело с агротехнологией, то такой целью может быть только получение заданного урожая культуры в конце вегетационного периода. Любая задача управления базируется на математическом описании ОУ. В рассматриваемом случае это сельскохозяйственное поле с агроценозом, в составе которого присутствует посев яровой пшеницы. Фундаментальной основой для решения задач программного управления служат математические модели, описывающие динамику параметров состояния объекта управления (ОУ). При этом кроме математической модели основной культуры, ОУ должен дополняться моделью сорных растений. Такие модели должны отражать влияние внешних неуправляемых возмущений, влияние управляемых воздействий на параметры состояния ОУ и учитывать их взаимосвязь между собой через почвенную среду.

Для достижения вышеуказанной цели управления прежде всего необходимо выбрать наиболее важные целеобразующие параметры состояния посева возделываемой культуры. При этом рассматриваемая культура характеризуется как континуальными параметрами состояния, к которым могут быть отнесены параметры состояния биомассы самого посева и почвенной среды, так и структурными состояниями, к которым относятся фенологические фазы развития (фенофазы). Для яровой пшеницы в зависимости от длительности интервала в суточном масштабе времени t таковыми состояниями являются: при t е (0-7) s = 1, фаза посев; при t е (11-13) s = 2, фаза всходы (1-й, 2-й, 3-й листы); при t е (21— 29) s = 3, фаза кущение; при t = 30 s = 4, фаза выход в трубку; при t е (31—32) s = 5, фаза междоузлие; при t = 37 s = 6, фаза флаговый лист; при t = 39 s = 7, фаза язычок; при t = 49 s = 8, фаза открытие листовой пазухи; при t е (51—59) s = 9, фаза колошение; при t е (61—69) s = 10, фаза цветение; при t е (71—75) s = 11, фаза молочная спелость; при t е (85—86) s = 12, фаза восковая спелость; при t >  86 s = 13, фаза полная спелость.

Весь период вегетации в зависимости от структуры биомассы посева может быть разделен на два интервала времени: со 2-й по 9-ю и с 9-й по 13-ю фенофазы. В то же время внесение удобрений, обработки гербицидами и поливы проводятся в фиксированные моменты времени наступления заранее выбранных следующих фенологических фаз: s = 3 (кущение), s = 9 (колошение), s = 10 (цветение), s = 11 (молочная спелость). Это заставляет прибегать к разбивке всего интервала управления на четыре интервала между выбранными фенофазами: 1-й — от кущения до колошения (Тз, Т9), 2-й — от колошения до цветения (Т9, Тю), 3-й — от цветения до молочной спелости (Т10, Ти), 4-й — от молочной спелости до полной спелости (Т11, Т13).

Для первого интервала времени для фенофаз с 3-й по 9-ю модель динамики параметров структуры биомассы посева имеет следующий вид (1, 2):

x lm

.x 2m J

+

с 11

с 21

a 11

a 21

с 12

с 22

a- a

22 _m

^C 13

с 23 _ m

x ( t ) x ( t )

1m

+

¹2m _

f 1 ( t ) f 2 ( t ) f 3 ( t )

—

b 11

b 21

d 11

d 21

b 12

b 22

d ₁ d ₂

22 J m

b 13    b 14

b 23    b 24

m

g ,⁽ t ) . g 2 ( t ) J m

v _N( t ) v _K ( t ) v _P ( t ) v _Mg ( t ) v ₅ ( t )

+

, t G (T 3 , T9),

где приняты следующие обозначения: x 1 m — средняя по площади поля плотность биомассы посева (урожайность), ц • га— 1; x2m — средняя по площади поля плотность сырой массы посева, ц • га— 1; внешними возмущениями в обоих блоках являются f1 — среднесуточная температура воздушной среды, °С; f2 — среднесуточный уровень радиации, Вт • (м2 • ч)—1; f3 — среднесуточ- ная интенсивность осадков, мм; параметры химического состояния почвы: vn — содержание азота в почве, кг • га—1; vк — содержание калия в почве, кг • га— 1; vр — содержание фосфора в почве, кг • га—1; vMg — содержание магния в почве, кг • га—1; v5 — влагозапас в почве, мм; g 1m(t), g2m(t) — дозы обработки гербицидами, г • га—1. В связи с научно-методическим значением настоящей работы мы не раскрываем здесь виды гербицидов, так как развиваемый нами подход реализуем для любых гербицидов.

Модель [1] для дальнейшего использования удобно представить в канонической символьной векторно-матричной форме, где все переменные объединены в векторы, а параметры — в соответствующие матрицы:

•                                                                                                         .                                                                                    .                                                                                 .                                                                                                .

X = A X ( t ) + B V( t ) + C F( t ) — D G ( t ).

m mm    m     m     mm .

Для интервалов со второго — ( Т 9 , Т 10 ), ( Т 10 , Т 11 ) и ( Т 11 , Т 13 ) — модели динамики параметров структуры биомассы посева имеют общий вид и различаются только значениями параметров (1, 2):

x 1 u x 2 u x ₃

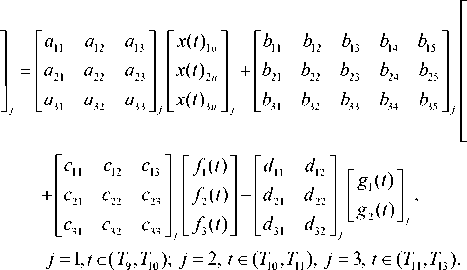
v N⁽ t ) ^v k ⁽ t )

V P⁽ t ) ^v Mg⁽ t )

^V 5⁽ t ) J j

+

В этой модели параметрами состояния являются x 1 u — средняя по площади поля плотность биомассы посева, ц • га - 1 ; x 2и — средняя по площади поля плотность сырой массы посева, ц • га - 1 ; x 3 и — средняя по площади поля плотность массы колосьев (урожая), ц • га - 1 ; внешними возмущениями в обоих блоках являются f 1 — среднесуточная температура воздушной среды, ° С; / 2 — среднесуточный уровень радиации, Вт • (м² • ч) ^{- 1}; f 3 — среднесуточная интенсивность осадков, мм; параметры химического состояния почвы: v n — содержание азота в почве, кг • га ^{- 1}; v к — содержание калия в почве, кг • га ^{- 1}; v p — содержание фосфора в почве, кг • га ^{- 1}; v Mg — содержание магния в почве, кг та ^{- 1}; v 5 — влагозапас в почве, мм; g 1u ( t ), g 2u ( t ) — дозы обработки гербицидами, г • га ^{- 1}; j = 1, 2, 3 — номера интервалов управления после фазы колошение.

Каноническая символьная векторно-матричная форма модели имеет следующий вид (3):

X uj = A uj X u ( t ) + B u V j ( t ) + C u F( t ) - D u G uj ( t ).                    [4]

Как было указано выше, кроме модели [4], для решения задачи необходима динамическая модель биомассы доминирующих видов сорняков, векторно-матричная форма которой имеет вид

S j = A, S j (T ) + B s V (T ) - B g G j ( t ) + C j F( t ),                      [5]

где ST= [s1 s2] — вектор биомасс доминирующих видов сорняков, T — индекс транспонирования вектора или матрицы,

A _	" an	0 "	,B _	- b 1	b 12	b 13	b 14	,B _	r b ,
s	_ 0	a 22 _	, s s	_ b 21	b 22	b 23	b 24 _	, g	0

0 _r _ c 11    c 12

’ s”

b 22 J g        L c 21    c 22

c 13    c 14

c 23    c 24

матрицы параметров модели.

Модель [5] включает в себя состояния двух доминирующих видов сорняков. Для других условий их число и виды могут быть другими, что только уточняет структуру алгоритмов, но не меняет общий подход к реше- нию задачи.

Модели [2], [4], [5] представляют основной блок параметров состояния ОУ. Кроме этого блока, ОУ содержит блок передачи управления, которым является почвенная среда (ПС). Именно через указанный блок осуществляется конкуренция растений культуры и сорной растительности за элементы питания и влагу.

Модель динамики параметров состояния почвы для фенофаз с 3-й по 9-ю приобретает следующий вид (1):

vN      Г a11   0    0 vK         0   a 22   0 vp         0    0 a 33 vM      0   0   0 A       0   0   0 L 5 _3,9    L ■  0   0   c13 " 0  0  c 23 +  00 c33 0    0   c43 _ c 51   C52    1 _3,9 0  a15 1 Г vN1 Г1   0  0  0  01  Г d N( t)" 0  a 25      vк       0  1  0  0  0     d k( t) 0  a 35      vp    + 0 0 1 0 0     d p( t)    + a 44  a 45     vMg       0 0 0  1 0     d Mg( t) 0 a55 J3,9 L v5 _3,9 L0 0 0   0  1_3,9 Ldw(t) J3,      [6] Г m11  0 1              Г p11   p12 1 fl(t)       m21   0      |-    (t )П    P21   P22 f2(t) - m31   0       x1 m( ) - p31   p32    S(t), ,                n      x2m(t) Lfi( t) J     m 41  0                  P41   P42 _m51   m52 J3,9              LP51   P52 J3,9 или в компактной символьной форме

V 3,9 = A 3,9 V( t ) + В з,9 D ( T 3 , T 9 ) + С з,9 F( t ) - М з,9 X „ ( t ) - P^ S( t).              [7]

	Модели динамики параметров состояния почвы для интервалов ( Т 9 ,
Т 10 ), ( значен ' L v +	т 10 ия 0 N ■ v K ■ v P Mg 5 " 0 0 0 0 _ c 51	, т ми 0 0 0 0 c 5	11 ) и ( Т 11 , Т параметров: "  а 11    0     0 0 a 22   0 00 a 33 0   0   0 _ 0    0    0 "      1 c 23       f ( t ) c 33       f 2 ( t ) c 43 L f > ( t ) . 2 1	13 ) имеют один и то 0 a i5 1 Г v N 1 Г 1 0 0   a 25      v к       0  1 0 a 35     v P + 00 a 44   a 45     v Mg       0  0 0    a55 , v .    0  0 55 j      5 j m 11  0 m 13 m 21 0 m 23     x 1 u ( t ) - m 31 0 m 33     x 2 u ( t ) m 41 0 m 43 L x 3 u ( t ) _ _ m 51 m 52    0 J ,	т же вид, р 0 0 0 1 0 0 0 1    0 0 0 1 0 0 0 1 Г P 11    P 12 P 21   P 22 - P 31   P 32 j     P 41    P 42 _ P 51    P 52	азличаясь только d n ( t ) " d k ( t ) d p ( t )    + d Mg ( t ) d w ( t ) , [8] S ( t ),

где d p( t ), d k( t ), d n( t ), d W ( t ) — дозы внесения элементов питания (соответственно фосфора P, калия K, мелиоранта Ca, азота N и магния Mg, кг • га - 1 ) и норма полива, мм; a 11 — a 33 , b 2 — b 3 , c 1 — c 3 — параметры модели, оцениваемые по экспериментальным данным; t — время, сут.

Модель [8] в компактной символьной векторно-матричной форме

V = — ( t ) + B j D - ( t ) + C - F( t ) - M - X - ( t ) - P - S( t ). [9]

Сложная многомерная структура ОУ, включающая модели [2], [4], [5] основного блока параметров состояния и блоки передачи управления [7], [9], приводит к необходимости решать задачу программного управления в два этапа (1, 2). На первом этапе находится программа потенциального развития посева культуры на всем интервале вегетации, обеспечивающая достижение поставленной цели управления. В этом случае не учитывается влияние сорной растительности, а в качестве управляющих переменных рассматриваются параметры состояния ПС без учета технологических ограничений. Полученная таким образом управляющая программа служит ориентиром для формирования последовательности технологических операций, включающих внесение удобрений, поливы и обработки гербицидами.

Поэтому на втором этапе находится последовательность технологических операций, которая должна обеспечивать минимальное отклонение параметров ПС от оптимальной программы, полученной на первом этапе. Такая декомпозиция задачи программного управления существенно упрощает синтез оптимальных программ управления. Кроме того, полученные на первом этапе результаты оптимизации как характеристика потенциального уровня урожайности культуры представляют самостоятельный интерес.

В соответствии со схемой динамического программирования (6) задача первого этапа решается от конца вегетационного периода к его началу. Целью управления при этом служит получение заданной урожайности культуры в конце интервала вегетации при выполнении следующих условий: достижение требуемой структуры всего биологического урожая (а именно требуемого количественного соотношения между зерном и соломой), требуемой влажности зерна, а также снижение биомассы сорных растений в агроценозе до заданного уровня.

В обозначенных параметрах состояния цель управления для указанного интервала вегетации формально выглядит следующим образом:

X u ( T 13 ) > 2,1 U • , х ₂ u ( T _B) < 0,15 U • , х 3 u ( T ^) > U • , S u ( Г _в) < S u , где U( T 13 ) — заданная урожайность, цта ^{- 1}; S Uj — заданная биомасса сорных растений.

Критерий оптимальности для межвегетационного периода с 9-й по 13-ю фенофазу, отвечающий поставленной цели, имеет следующий вид:

J u T = [X u T - x;( T 3 )]^T G u [X u ( T 13 ) - X ;. ( T 13 )] + +[s „( 2 ^3 )] - s u ( T 3 )] ^T Q [S uj ( T 13 )] - s ". ( T 13 )],

где X * T = [2,1 U 0,15 U U ] — вектор, компонентами которого служат общая биомасса, сырая масса, масса зерна (урожай);

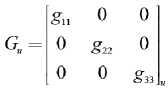
q 1

q 2

– весовая матрица массовых и качественных составляющих критерия,

– весовая матрица компонентов биомассы сорных растений, j = 0,1,2,3 – индексы интервалов управления.

Для формирования оптимальных программ на всех интервалах управления используется принцип максимума Понтрягина (6). В соответствии с этим методом гамильтониан системы, включающей в себя модели

[4], [5] и критерий [10], имеет следующий вид:

H uj (t ) = A juj X uj (t ) + B uj V j t ) + C uj F( t ) - D uj G uj (t )] +

■A u [A , S ₄(T ) + B , V uj ( T ) - B g G j ( t ) + C , F(T)].

а модели сопряженных переменных — соответственно

^A_M= 3, =-H ^uj = ^3,L = -^A T^T= 3, ^A > u = 3 i , t £ (^T_xv^T 13 ), A __3/( 7 13 ) = [X „j (^T 13 ) - ^X • ] ,      [12]

d X1,uj =3, i                                                             Vuj ' i ah a 2uj=3,=-^Hj3L = -AT=3,iA2uj=3„ t £ (T11, T13), A     (T13) = 2[Suj(T3)] - S"].      [13]

^d ^ 1,uj = 3, i                                                                   ², uj , i

Алгоритм формирования оптимальной программы изменения параметров почвенной среды, обеспечивающей достижение цели управления, включает в себя следующие итерационные процедуры:

• 1)    формирование оптимальных программ изменения параметров ПС: v*. + 1 ( t ) = v:„ ( t ) -A , GR u, , ( t ),

^GR uji (t ) = ^T" ( t ) = ^{B T} uj ^A 1 uj,i ( t ) + ^{B T} . A ₂» , ( t ). ^V uj, I

• 2)    поиск начальных условий на границах фенофаз:

X j,++1(T1j = X ;„ (T11)-A i A1u„ (T11), sji+1(T11) = Sji, (T11) -A, A 2uj, (T11).

В результате решения задачи первого этапа формируется оптимальная программа изменения вектора параметров ПС V*(t), состоящая из отдельных кусков на четырех интервалах управления между выбранными фенофазами. Этой программе соответствуют программа изменения вектора параметров состояния посева X*(t) и программа изменения вектора параметров биомассы сорняков S*(t) на этих интервалах управления.

Достижимой целью управления на втором этапе общего решения задачи является обеспечение наиболее близкого приближения к оптимальным программам содержания элементов питания и влаги в почве, полученным на первом этапе прогнозных программ, полученных за счет независимого выбора доз подкормок и поливов. При этом внесение удобрений и поливы проводятся в фиксированные моменты времени наступления следующих фенологических фаз: s = 3 (кущение), s = 9 (колошение), s = 10 (цветение), s = 11 (молочная спелость).

Как и для первого этапа, задача решается отдельно для каждого ин- тервала управления, но уже в прямом направлении — от начала периода вегетации к его концу.

Частные критерии оптимальности для каждого j -го интервала управления имеют один и тот же вид:

T

J j = J [(V ; ( t ) - V j ( t )) ^T G ; (v ; ( t ) - V/ t )) + c_d D ; (t)dt , ; = o,i,2,3,

^G; =

" g 1	0	0	0	0
0	g 2	0	0	0
0	0	g 3	0	0
0	0	0	g 4	0
0	0	0	0	g 5

— весовая матрица, Cd — вектор цен на единицу доз.

Критерий [17] формируется посредством модели параметров состояния почвы [9]:

V=a,v/ t)+Bj Dj( t)+Cj F( t) - Mj x; (t) - Pj s; (t), где X*j(t), S *j(t) — оптимальные программы параметров состояния посевов и сорняков, полученные на первом этапе.

Гамильтонианы для всех интервалов управления одинаковы:

H j = [(V * ( t ) - V ; ( t )) ^T G ; (V ; ( t ) - V ; ( t ^ + CD ^ t ^ + ♦^[A ;^t ) + B ; D ; ( t ) + C ; F( t ) - M ; X * ( t ) - P ; S^ j ( t )],

T где Vj — векторы сопряженных переменных на j-х интервалах управления.

Модели сопряженных переменных имеют следующий вид:

Алгоритм формирования последовательностей доз внесения удобрений (оптимальных программ управления) включает в себя итерационную процедуру последовательного поиска очередных приближений векторов доз внесения удобрений и поливов:

D;__x (T_v) = D; ЛТ_м ) - △ : ( C_D + ВJ Ф_v (Г,,)), если D^^eQ,;

ПЖ>П*(Т_ц), если С^-)^,-

В результате решения задачи на втором этапе формируются последовательности доз внесения удобрений и поливов по всем интервалам управления D ^* j ( T 1 j ), j = 0,1,2,3, которым соответствуют программы изменения параметров почвенной среды V ^* j ( t ), параметров состояния посева X ^* j ( t ) и параметров биомассы сорняков S ^* j ( t ).

Найденная оптимальная последовательность технологических операций (программа) пока не учитывает прямое влияние гербицидов на состояние посева культуры в соответствии с моделями [2], [4]. В начале процедуры формирования программы управления такое влияние невозможно учесть, так как дозы обработок априорно не известны. Поэтому необходимо ввести еще один внешний оптимизационный цикл, в котором такое влияние учитывается. Для этого необходимо замкнуть всю процедуру формирования оптимальной программы управления по дозам обработки гербицидами.

Для решения задачи используются модели [4], [5]

X uj = A uj X uj ( t ) + B uj V * ( t ) + C uj F( t ) - D uj G^(t ) , S y = A , S , ( t ) + B , V J ( t ) - B _g G j ( t ) + C , F( t ), где V^* j ( t ) – оптимальная программа изменения параметров почвенной среды, полученная на втором этапе.

Целью управления на рассматриваемом этапе служит выбор таких доз обработок гербицидами на всех интервалах управления, которые обеспечивают наилучшее приближение прогнозных программ изменения параметров состояния посевов и параметров биомассы сорняков к оптимальным программам, найденным на втором этапе.

Этой цели соответствует следующие критерии оптимальности на отдельных интервалах управления:

^T 2j

J j = J [(X ’ ( t ) - X/ t )) ^T G_v(X j ( t ) - X/ t )) + (S j ( t ) - S j ( t )) ^T G_{2 y} (S ; ( t ) - S j ( t))dt ,

T                                                              ^[21]

j = 0,1,2,3

Алгоритм формирования программ обработки гербицидами представляет собой следующую итерационную процедуру:

G*,i+i(Tj = G*,i(Ti)-^i GRj,i(Tij), ан

GR ji (Tx) = ^ ( T ij ) = D ^ iA ) + B , 'I- 2 j , i ( T 1 j ).

На первом этапе формирование программ внесения удобрений проводилось без учета программ обработки гербицидами. С учетом того, что внесение удобрений и обработки гербицидами осуществляются одновременно, программы внесения удобрений требуют коррекции по программам обработок гербицидами. Для этого в алгоритм вводятся три глобальных шага.

Шаг 1. Принимается глобальная циклическая переменная k = 1. Программа обработок гербицидами G *( T 1 j ) по всем интервалам управления подставляется в интервальные модели, решая их от начала j = 0 до конца j = 3:

^X _MJ=A _UJX _uj( t ) + B uj V ( t ) + C,F( t ) - D ₄G₄< t ), t E ( T J , T 2 J ),      [23]

S j =A , S j ( t ) + B , V j ( T ) - B g G j ( t ) + C , F(T), t e (T j , T 2 j ) ,        [24]

при этом конечные решения на текущем интервале принимаются в качестве начальных для последующих интервалов: X0(T1j+1) = X(T2j), S0(T1j+1) = S(T2j). На начальном интервале принимаются общие для всей задачи начальные условия: X0(T1j = 0), S0(T1j = 0). Для интервала управления принимается глобальная циклическая переменная k = 1, j = 3 вычисляется критерий в конце интервала вегетации:

J _k =i ( T _n) = [X uj = 3 ( T i3 ) - x uj .= 3 ( T i3 )]^T G u [X uj = 3 ( T i3 ) - X ^j, = 3 ( ^ 3 )] +

+ [S uj = 3 ( T 3 )] - S V = 3 T 3 )] ^T 6 (S ^ = 3 ( ^ 3 )] - S V ₌ 3 ( T b)].

Шаг 2. Если критерий J k = 1 ( T 13 ) меньше заданной величины Δ , то СТОП, иначе решения моделей [4], [5] переносятся в пункт 1 первого этапа, и все этапы задачи повторяются вплоть до получения нового критерия J k = 2 ( T 13 ).

Шаг 3. Если критерий J k = 2 ( T is ) меньше критерия J k = 1 ( T is ), то требуется перенос решений моделей [4], [5] в пункт 1 первого этапа, иначе СТОП, и принимаются решения для предшествующего критерия J k = 1 ( T is ).

Результаты . Результат настоящей работы — предложенный алгоритм программного управления состоянием агроценоза с посевом яровой пшеницы. Этот алгоритм воплощает новую теорию управления агроценозом и реализован в новом специализированном программном продукте. Новизна и сложность алгоритма требует его апробации по экспериментальным данным, что должно отражать возможность использования полученных результатов в реальном производстве.

По своей сути апробация заключается в установлении факта устойчивости алгоритма управления и его сходимости к минимуму выбранного критерия оптимальности. Эти условия могут быть получены только при качественной идентификации всех используемых в задаче математических моделей. Она проводилась по экспериментальным данным, полученным за 2015-2021 годы в Меньковском филиале Агрофизического института (Ленинградская обл.).

На диаграммах (рис. 1, 2) приведены результаты оптимизации программ управления агроценозом, включающие в себя последовательности доз внесения минеральных удобрений, поливов и обработок гербицидами. Программа ориентирована на получение заданного урожая зерна 30 ц/га.

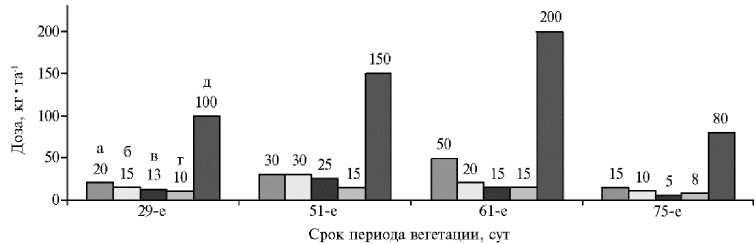
Рис. 1. Оптимальная программа единого управления агроценозом по дозам внесения минеральных удобрений и поливам: а, б, в, г — дозы внесения соответственно азота, калия, фосфора и магния; д — норма полива, т•га ^{- 1}.

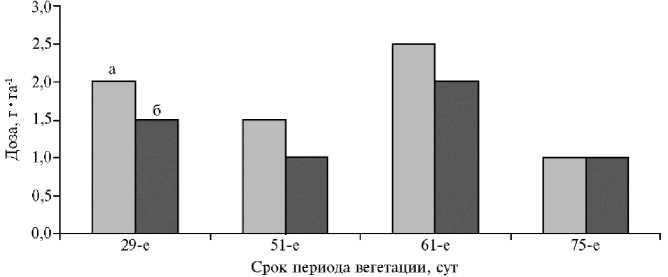
Рис. 2. Оптимальная программа единого управления агроценозом по дозам обработок гербицидами: а — доза внесения гербицида 1, б — доза внесения гербицида 2 .

Здесь технологические операции проводились в моменты наступления фенофаз: t = 29 сут (кущение), t = 51 сут (колошение), t = 61 сут (цветение), t = 75 сут (молочная спелость).

Этим программам соответствует прогнозная динамика параметров биомассы посева яровой пшеницы и двух доминирующих видов сорняков (рис. 3, 4).

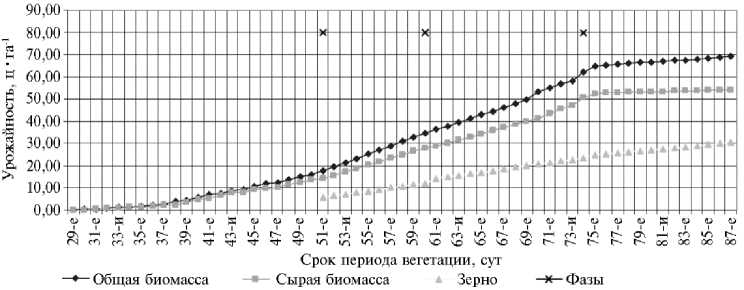
Рис. 3. Динамика параметров биомассы посева яровой пшеницы при оптимальной программе единого управления агроценозом.

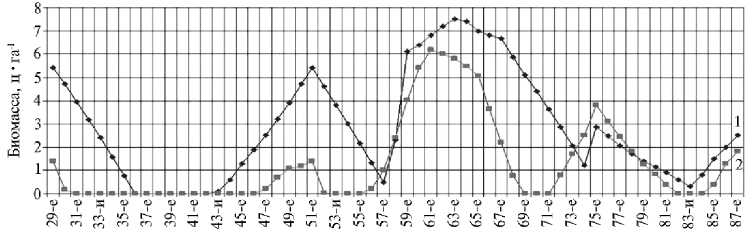
Срок периода вегетации, сут

Рис. 4. Динамика параметров биомассы доминирующих видов сорняков при оптимальной программе единого управления агроценозом: 1 — сорняк 1, 2 — сорняк 2.

Приведенные оптимальные программы управления получены для 3х итераций глобального цикла алгоритма, чему соответствовали следующие значений критерия оптимальности [10] для заключительной фенофазы посева: итерация 1 — J u = 32 (ц/га)², итерация 2 — J u = 14 (ц/га)², итерация 3 — J u = 6 (ц/га)². Заметим, что все используемые критерии оптимальности являются квадратическими функциями, поэтому размерность их урожайности взята в квадрате. Убывание критерия оптимальности по итерациям глобального цикла алгоритма доказывает его устойчивость и последовательное приближение к минимуму критерия оптимальности.

Как видно из представленного графика (см. рис. 3), оптимальная программа по одновременному внесению удобрений, поливам и обработкам гербицидами обеспечивает плавный рост и развитие посева яровой пшеницы от всходов до заданного урожая 30 ц/га. На следующем графике (см. рис. 4) видно, что сорняки более динамично реагируют на технологические операции оптимальной программы, где стимулирование минеральными удобрениями и поливами вызывает рост биомассы сорняков, который подавляется дозами обработок гербицидами. При этом в агроценозе проявляется общая тенденция к снижению биомассы сорняков к концу периода вегетации.

По результатам апробации задачи можно утверждать, что предложенный алгоритм и специализированный программный комплекс обладают характеристиками, достаточными для применения этой разработки в качестве средства интеллектуальной поддержки специалиста-агронома.

Алгоритм и программный комплекс, разработанные нами, соответ- ствуют концепции превентивного управления, которое рассматривается как основной перспективный подход в мероприятиях по защите посевов от сорняков (20).

В литературе представлен ряд моделей, которые позволяют с определенной степенью достоверности количественно оценить вероятность результатов для принятия обоснованных решений, сравнивать различные методы управления и выбирать варианты с наибольшим долгосрочным эффектом в отношении целевой группы применительно к сельскохозяйственным объектам (20). Избранные примеры дают общее представление о моделях, описывающих распространение сорной растительности в посевах, использовании таких моделей в ключевых областях управления в растениеводстве, полученных количественных выводах и прагматических результатах (20). Однако важно признать, что лишь небольшая часть моделей (включая когда-либо разработанные СППР) широко применялась для решения реальных проблем борьбы с вредными организмами (38-41). Главными причинами называют то, что практические специалисты считают модели не соответствующими местным условиям и не располагают временем для изучения типовых операционных процедур; в моделях не учитываются изменения, происходящие в структуре и численности популяций сорных растений, в экономике растениеводства, недостаточно поддерживаются стандарты программного обеспечения (50-53).

Как видно из анализа доступных публикаций, все известные до настоящего времени модели предназначены для отдельных систем в земледелии и растениеводстве (культурные растения—сорняки, культурные растения— удобрения, сорняки—гербициды). Нами поставлена и решена принципиально новая задача и разработана программа единого управления агроценозом (система культурные растения—сорняки—удобрения—гербициды), объединяющая перечисленные частные задачи. Новизна изобретения подтверждена патентом РФ ¹ 2772889 «Способ одновременного дифференцированного внесения жидких минеральных удобрений и гербицидов и устройство для его осуществления» (от 26.05.2022). Результаты апробации показали возможность применения этой разработки в производственных условиях.

Таким образом, нами предложена новая теория программного управления агроценозом, ориентированная на реализацию технологической идеи совместного внесения минеральных удобрений и обработок гербицидами. Она включает новые математические модели параметров состояния возделываемой культуры и сорной растительности в составе агроценоза, а также новые алгоритмы формирования оптимальных программ управления. Алгоритмы представляют собой четырехэтапную процедуру последовательного формирования программы потенциального развития посева культуры, формирования последовательности технологических операций без учета обработок гербицидами и программы последовательности обработок гербицидами, проводимыми вместе с внесением удобрений и поливами, а также коррекцию программ технологических операций по программе обработок гербицидами. Предложенный алгоритм формирования оптимальных программ управления позволяет избежать проблемы большой размерности и сложности общей задачи управления и обеспечить его устойчивость, достижение заданной урожайности культуры и минимизации биомассы сорной растительности. Полученные результаты являются существенным вкладом в современную цифровизацию и интеллектуализацию управления агротехнологиями в точном земледелии.