Производственная функция с учетом ограничения производственных мощностей по возрасту

Для учета переходных процессов в математическом моделировании экологоэкономических систем важно уметь описывать структурные изменения в производстве, например, за счет агрегирования микроописания динамики производственных мощностей. Описание производственных функций, представимых распределением производственных мощностей по технологиям, возникло из практических нужд при анализе конкретных отраслей экономики [1–2]. Производственная функция такого типа для одной переменной

«Московский физико-технический институт (государственный университет)», 2017

используется в [3] при макроописании экономики. Математическое исследование такого рода производственных функций для многих переменных произведено в [4–5], при этом доказана взаимная однозначность производственных функций и функций прибыли.

Новый класс производственных функций, представимых распределением производственных мощностей по технологиям, получен в [6] на основе исходного микроописания. Получено параметрическое выражение для производственной функции в случае, когда микроописание производственной единицы основано на гипотезе о фиксированном с момента создания числе рабочих мест и падающей с постоянным темпом мощности. Аналитическое выражение для производственной функции в случае, когда мощности не ограничены по возрасту, получено в [6] на режиме сбалансированного роста.

Если в каждый текущий момент времени t обозначить выпуск (объем произведенной продукции или валовой внутренний продукт) через Y ( t ), число рабочих мест (число занятых в экономике) — через L ( t ), а суммарную мощность — через M ( t ), Y ( t ) < M ( t ), то производственная функция задает зависимость выпуска Y ( t ) от производственных факторов M ( t ), L ( t ):

Y ( t ) = M ( t ) f ( t,x ) , (1) где x = L ( t ) /M ( t ) — средняя трудоемкость имеющихся мощностей, а f ( t,x ) — загрузка суммарной мощности (удельная производственная функция).

В [6] рассмотрен режим сбалансированного роста с темпом γ в замкнутой экономике, в которой выпуск Y ( t ) делится на потребление C ( t ) и накопление bl ( t ):

Y ( t ) = C ( t ) + bl ( t ) ,

где b >  0 — коэффициент приростной фондоемкости, а I ( t ) — объем вновь созданных производственных мощностей. На режиме сбалансированного роста все объемные показатели продуктового баланса (выпуск Y ( t ), суммарная мощность M ( t ), потребление C ( t ) и накопление bl ( t )) растут с одним и тем же темпом ү .

В случае мощностей, не ограниченных по возрасту, для функции загрузки суммарной мощности в [6] получено выражение f (t,x) = 1 - [1 - (1 - е - ц/а)Г'(1 ' "'”) ,                     (3)

^{v (} t )

где ц — темп падения мощностей вследствие износа, а = I ( t ) /M ( t ) — доля новых мощностей в суммарной мощности, а = ү - ц , v ( t ) — наименьшая трудоемкость, динамика которой определяется темпом научно-технического прогресса ε [6]:

dv ( t ) dt

- Eav ( t ) .

В соответствии с (1) - (4) этот режим сбалансированного роста с темпом ү = а + ц при наличии научно-технического прогресса (0 < Е <  1, ү > ц (2 - е ) / (1 - е )) характеризуется темпом изменения числа занятых в экономике А = ү - Ea и темпом роста £ = Еа >  0 среднего потребления. При отсутствии НТП ( е = 0) функция (3) f ( x ) обладает свойствами классической производственной функции и, кроме того, содержит среди параметров темп роста. Это делает рассмотрение «золотого правила роста» интереснее [6].

В [7] численно построенная эндогенная производственная функция с учетом ограничения мощностей по возрасту использовалась в оценке реального сектора экономики. Численные эксперименты [7], связанные с идентификацией параметров, показали два существенных факта. Во-первых, практические расчеты ведут с ограниченным возрастом мощностей. При этом достаточно рассматривать фиксированный максимальный возраст мощностей. Во-вторых, при рассмотрении динамики экономики на интервале в несколько десятилетий нужно учитывать изменение (как правило, снижение) коэффициента приростной фондоемкости.

В настоящей работе построим производственную функцию на режиме сбалансированного роста для мощностей, ограниченных по возрасту. Учет ограничения мощностей по возрасту дает не только дополнительное управление экономической системой [6], но и позволит определить параметры этой производственной функции при ее численном построении на основе статистических данных. Рассмотрим также переходный режим роста с уменьшающимся коэффициентом приростной фондоемкости. Идентифицированную производственную функцию можно использовать на практике для анализа конкретных экономических систем и для сценарных прогнозов.

2.    Описание процесса изменения производственных мощностей с учетом ограничения по возрасту

Для микроописания динамики производственной мощности воспользуемся предложенной в [6] гипотезой об ее уменьшении вследствие старения и фиксированном с момента создания этой мощности числе рабочих мест на ней, то есть здесь мы не учитываем рост производственной мощности за счет обучения во время работы [8].

Гипотеза 0. Число рабочих мест на производственной единице остается неизменным с момента ее создания т С t, а производственная мощность m ( t, т ) падает с постоянным темпом ц >  0 .

Поскольку начальная мощность m ( t, t ) = I ( t ) для каждого момента времени t , то в силу гипотезы 0 в дальнейшем мощность падает: m ( t, т ) = I ( т ) exp( —ц ( t — т )). Это падение мощности для сохранения числа рабочих мест требует соответствующего роста трудоемкости: А ( t, т ) = v ( т ) exp( ц ( t — т )), где v ( т ) — трудоемкость на производственной единице в момент ее создания τ . Напомним [6], что инвесторы в каждый момент времени выбирают наилучшую из существующих технологий, то есть технологию с наименьшей трудоемкостью v ( t ), а эта наименьшая трудоемкость со временем уменьшается в силу научно-технического прогресса с постоянным темпом ест ( t ) >  0 в соответствии c уравнением (4).

Если максимальный возраст мощностей, допускаемых к эксплуатации, обозначить A ( t ), то суммарная мощность равна

М ( t ) = -    I ( т ) e- ^{1 (} * ^-T ) dт.

Динамика мощностей в силу (5) описывается дифференциально-разностным уравнением

Ml = I ( t ) — цМ ( t ) - (1 - A )) I ( t — A ( t )) e ^{-1A (} * ' , dt                              dt

где dA/dt С 1. Последнее условие означает, что мощности, однажды превысившие A(t), демонтируются и в производство не возвращаются, а A(t) является дополнительным управ- лением.

В соответствии с [3-6] считаем, что используемые трудовые ресурсы L(t) загружаются оптимальным образом, начиная с только что созданных мощностей нулевого возраста с наи- лучшей технологией (наименьшей трудоемкостью) до мощностей возраста Ө (t, L (t)) С A(t), так что система уравнений для выпуска Y (t) и труда L (t) определяет выражение для про- изводственной функции:

Y (t) = Г t—Ө (*,L (*))

I ( т ) е ^{-1 (} * ^-т ) dт,

f ( t, x ) = Y ( t ) /M ( t ). В силу (4) имеем v ( т ) = v ( t ) exp ( e J t a ( s ) ds J. Тогда из (7) - (8) получим параметрическое выражение для производственной функции:

t

f(t-x )=m^ L (tx>M(т) e-(T>dT,

t

= MM        M(т)a(т)e'T-°('>d*d^(10)

^{v (} t )      M ⁽ t ) t — Ө ( _t,x )

Дифференциально-разностное уравнение (6) для суммарной мощности М ( t ) в интенсивных переменных выглядит следующим образом:

1 і^ = a (t) _ ц - Л - A) A a (t - A(t)) M (t - A(t)).

M (t) dt                         dt )M

Как уже говорилось во введении, численные эксперименты по определению параметров численного представления производственной функции (9) – (10) для ряда стран (см., в частности, [7]) показали, что наибольший возраст мощностей A ( t ) на интервале времени в несколько десятилетий можно считать фиксированным для каждой страны на своем исторически сложившемся уровне, связанном с международным разделением труда. Поэтому дальнейшие выкладки будут производиться в предположении, что A ( t ) = A = const.

Тогда дифференциально-разностное уравнение для мощностей с фиксированным максимальным возрастом примет вид dMdtt = (a(t) - ц) M(t) - a(t - A)M(t - A)e-^A                 (11)

с начальным условием M ( t ) = ф ( t ) при -A ^ t ^ 0.

• 3.    Эндогенная производственная функция на режиме сбалансированного роста с постоянной фондоемкостью

Рассмотрим режим сбалансированного роста с темпом γ , в котором коэффициент приростной фондоемкости не меняется: b ( t ) = b = const.

M(t) = MоeYt, Y(t) = Y)eYt, I(t) = IоeYt, C(t) = CоeYt.(12)

Тогда условие a ( t ) = a = const и (11) дает связь темпа роста ү с параметрами a, ц, A :

ү + ц = a (1 - e-(Y+^)A) ,(13)

а соотношения (9), (10) дают выражение для производственной функции:

f (t,x) =       (, - [1 - (1-^    1 -1Y+">/(   '>1

ү + ц               av где темп сбалансированного роста ү = ^ (a, ц, A) — неявная функция параметров a, ц, A, определяемая в силу (13). Из соотношений (13), (14) непосредственно следует

Утверждение 1. Новая производственная функция на сбалансированном росте (14) с учетом ограничения мощностей по максимальному возрасту A и с фиксированным коэффициентом фондоемкости b при A →∞ дает производственную функцию с неограниченными по возрасту мощностями (3) , полученную в работе [6] .

Справедливо также

Утверждение 2. На сбалансированном росте с фиксированным коэффициентом фондоемкости b число занятых в экономике трудящихся L(t) за счет научно-технического прогресса растет с темпом п = ү — ест, а средний уровень потребления занятых с темпом £ = ест.

Доказательство. Действительно, на режиме сбалансированного роста загрузка суммарных мощностей не меняется, f ( t,x ) = const, поскольку выпуск Y ( t ) и суммарные мощности M ( t ) связаны равенством (1) и в силу (12) растут с одинаковым темпом ү . Из (14) следует, что x/v ( t ) = const. В силу (4) v ( t ) = v о exp( —ECTt ). По определению x = L ( t ) /M ( t ), поэтому труд L ( t ) растет медленнее, чем выпуск Y ( t ):

L ( t ) = L о e ^{( Y-£CT} ) t .

Из (15), (12) вытекает, что средний уровень потребления c ( t ) = C ( t ) /L ( t ) = c о , '^ .

Соотношения (15), (16) есть то, что и требовалось доказать.

Из (13), (14) можно исключить ст = ( ү + ц ) / (1 — exp( — ( ү + ц ) A )), представив производственную функцию в виде

'                                                                   1 _{- e} - ( Ү + М ) A      '

- 1 — [1 — ((1 — е-(Ү+")A) ч+ц — е) VxT)] (1 -e-("+')A)■- - f (t,x) = ----------------------------------------------------------- v 7                                  1 — е-(Ү+V-) A

Это выражение для производственной функции в явном виде содержит темп роста γ и может быть использовано в анализе «золотого правила накопления» Э. Фелпса.

4.    Переходный режим с уменьшающейся фондоемкостью

В вычислительных экспериментах, связанных с идентификацией параметров численного представления производственной функции для ряда стран мира [7, 9], был обнаружен характерный режим роста, в котором мощности и выпуск растут с постоянным темпом, доля новых мощностей не меняется, а коэффициент фондоемкости падает. В этом режиме рост не сбалансирован, доля суммарного потребления растет, а доля накопления падает. Это не привычная магистраль, рассмотренная в предыдущем параграфе, а некоторый переходный режим, видимо, ограниченный по времени.

Рассмотрим этот переходный режим роста, в котором под влиянием научнотехнического и социального прогресса коэффициент приростной фондоемкости со временем падает:

b ( t ) = b о e -^et , (17)

где в >  0 — темп падения, а b о — начальное значение коэффициента приростной фондоемкости. При этом суммарная мощность и суммарный выпуск растут с одинаковым постоянным темпом γ :

M ( t ) = M о e ^Yt , Y ( t ) = Y о e ^Yt , (18)

а доля новых мощностей и максимальный возраст мощностей остаются постоянными:

I ( t ) M ( t )

= const ,

A = const .

Для переходного режима эндогенного роста (17) – (19) справедливо следующее

Утверждение 3. Пусть на переходном режиме в замкнутой экономике коэффициент фондоемкости b ( t ) падает с постоянным темпом в в соответствии с (17) , выпуск Y ( t ) и суммарные мощности M ( t ) растут с постоянным темпом ү в соответствии с (18) , доля новых мощностей σ и максимальный возраст мощностей A не меняются, кроме того, действует научно-технический прогресс (4) . Тогда справедливы следующие утверждения:

• 1.    Темп роста определяется соотношением ү = ^ (ст, A) — ц, где ^(ст, A) есть единственное решение трансцендентного уравнения 1 — ^/ст = exp(—^A) на интервале ^ Е (0, ст) при естественном условии существования решения A > 1 /ст.

• 2.    Производственная функция на переходном режиме имеет вид (14), отношение средней трудоемкости к наименьшей: x/v (t) = const, темп роста числа трудящихся, занятых в экономике: п = Y — ест.

• 3.    Доля потребления в выпуске C(t)/Ү(t) увеличивается, доля накопления b(t)I(t)/Ү(t) уменьшается, а среднее потребление c(t) = C(t)/L(t) растет с темпом, превышающим εσ.

5.    Оценка параметров производственной функции по данным российской экономики

Доказательство. Действительно, темп роста γ в соответствии с (18), (19) и (11) определяется соотношением (13). Обозначив ^ = ү + ц , из (13) сразу же получим уравнение 1 — ^/ст = exp( —^A ), которое имеет единственное положительное решение, если производная левой части этого уравнения больше производной правой части при ^ = 0, что дает условие A >  1 /ст .

Второй пункт утверждения 3 следует из подстановки (18), (19) в параметрическое выражение для производственной функции (9), (10). В результате получим соотношение (14), что позволяет воспользоваться выражением (15) и утверждением 2.

Для доказательства третьего пункта заметим, что из первого равенства в (19) следует, что темп роста новых мощностей I ( t ) совпадает с темпом роста суммарной мощности M ( t ), а в силу (17), (18) доля накопления в выпуске падает: b ( t ) I ( t ) /Ү ( t ) = ( b q I q /Yq ) exp( —et ), соответственно, доля потребления C ( t ) /Ү ( t ) = 1 — b ( t ) I ( t ) /Ү ( t ) растет. Среднее потребление на переходном режиме в силу второго пункта определяется соотношением

_ f(x/v(t)) — стЬоe ^ eat ( ) vоx/v (t) ’ то есть среднее потребление на переходном режиме (при x/v(t) = const) растет быстрее, чем на режиме сбалансированного роста (16). Что и требовалось доказать.

Идентификация параметров численного представления производственной функции в реальных условиях была проведена по данным российской экономики [9]. Предполагая, что загружены все мощности до возраста, определяемого реальным выпуском, находился максимальный возраст из загруженных рабочей силой мощностей. Соответствующий объем рабочей силы подсчитывался и сравнивался со статистикой. Параметры выбирались так, чтобы отклонение расчета от статистики было минимальным. При этом для ускорения расчета использовались параллельные вычисления в интерфейсе MPI. Приведем здесь только предварительные результаты идентификации параметров по данным экономики России 1970-2014 гг.: b о = 5 . 625, в = 0 . 04025, v о = 0 . 004725, е = 0 . 2550, ц = 0 . 03125, A = 25.

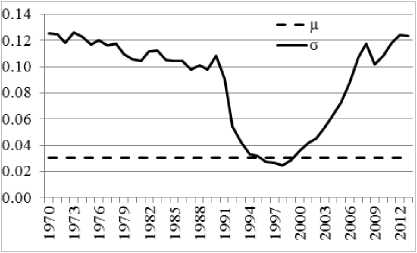
Рис. 1. Динамика доли ст ( t ) новых мощностей в сравнении с темпом падения мощностей ц для российской экономики

Реальный сектор российской экономики в 1970–2014 гг., как показали численные эксперименты, близок к аналитически исследованному выше переходному режиму с долей новых мощностей ст ~ 0 . 11 (рис. 1) на интервалах 1970-1990, 2007-2014 гг.

Кроме того, из рис. 1 видно, что доля новых мощностей ст ( t ) на интервале 1991-2006 гг. испытывает падение до «дна», определяемого темпом выбытия мощностей вследствие износа μ , а затем рост до «потолка», определяемого некоторым естественным уровнем загрузки мощностей. Подробный анализ соответствующих численных экспериментов и полученных результатов будет представлен в отдельной публикации.

6.    Заключение

Идентификация классических производственных функций по данным конкретной экономики в 60-е годы XX в. показала, что рост объемов используемых факторов производства в них не объясняет рост экономики [10]. В результате для объяснения экономического роста стали использовать экзогенные величины или рассматривать двухсекторную модель с секторами производства и образования, учитывающую роль человеческого капитала [10].

В настоящей работе рассмотрена еще одна возможность объяснения экономического роста за счет учета трех экзогенных механизмов технологического прогресса: 1) рост производительности труда на новых мощностях, 2) ограничение возраста использования мощностей, 3) снижение фондоемкости создания новых производственных фондов.