Производственные сети

N = (0, 1, 2, _, n ) и заданной числовой реализацией f C ^ X, т.е. имеет место факторизация

X = F(Ob/N) = U ne« X n                      (1)

(р с гомологией Xt ^ Xk, I > к Б N, где ф принадлежит множеству связей Ф. Таким образом, комплекс рассматривается как сеть обратного распространения с оцифровкой малой категории C=(Ob, SR) функтором F(C) = (X , Ф), гомологически представимая диаграммой в виде градуированного пучка с резольвентой X*

<р          р          <р<р

0 чХп 4 Xn-1 ^ Xn-1 ^ - чХ0 ^ °,   Р ^ Ф, с коэффициентами на гомоморфном пучке N*

<р      <р       <р     <р       <р<р

° ^ Nn ^ —^ Nl ^ — ^ Nk ^ —^ N0 ^ °, где |Nk| = nk и общее количество слоёв расслоения комплекса равно

n = |N| = n0 + n1 + —+ nn.                         (4)

При различных значениях n будем получать различные расслоения (1) и, как следствие, различные выражения (3) и (2). Имеет место и представление

p

0 ^ Xn ^ Xo ^ 0.

p      p   p

В последнем случае расслоение X_n-1 ^ X_n-1 ^ ... ^ X 1 становится внутренним расслоением X и само служит комплексом. Не нарушая общности можно полагать, что любой слой X k ^ X является комплексом и имеет внутреннюю топологию со своей пространственно-временной структурой.

Поскольку цепь (3) непрерывна, то X k содержит по крайней мере один объект, т.е. n k >  0 для любого k е N . Но, любой объект - суть количественно определённое качество и, если количество равномерно квантуется на порядковой шкале, то качество равномерно кантуется на произвольной замкнутой без точек самопересечения пространственной кривой, разрывая которую по произвольному звену, кривую можно расправить в отрезок и каждый слой представить отрезком, изобразив сеть C плоской диаграммой. Представление сети с двумя скрытыми слоями изображена на рис. 1.

Рис.1. Сеть обратного распространения с двумя скрытыми слоями.

Пусть l > k е N и i е N_k . Для смежных элементов слоя Ni элементу i введём обозначение N_li . Тогда

^ = 11 Nf xl = \\ Х?

jeNk ^к^к

И если l > t > к и имеют место множества N it , N_tk , то существует производственная цепь движения ресурсов от производственного узла X f е Xi_t к смежному узлу x_h е X k с их промежуточным преобразованием в скрытом узле x g еX_tk , представленная на диаграмме (рис.2.)

X f

ф ⁽ x f )

X g

Ф( Х д )

X h

Рис. 2. Схема движения ресурсов по производственной цепи с их преобразованием в промежуточном узле.

С технической точки зрения функция ф является трансляционной, но может выполнять роль активации предшествующего узла по типу функции Хэвисайда. В простейшем случае работу схемы можно представить в виде линейной модели Мак-Клока-Питца, где каждый узел является сумматором ресурсов, поступающих от смежных с ним нижестоящих по иерархии узлов [1, стр. 45].

Работа производственного узла представим рис. 3.

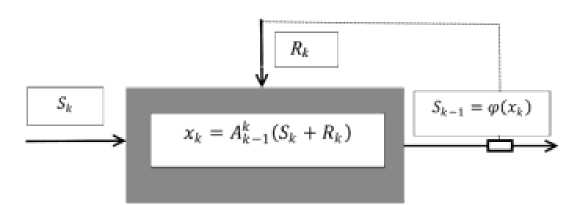
Рис. 3. Схема работы узла с обратной связью.

Здесь S (средства труда) и внешние R (трудовые ресурсы) ресурсы под воздействием средств производства A вступают во взаимодействие и переносят свою стоимость в стоящие выше по иерархии смежные с ним узлы. Вместе с данной стоимостью переносится и стоимость амортизации средств производства. Таким образом, модель работы объекта описывается линейной матричной моделью, в которой величины S и R выступают в качестве векторов, а средства производства A - матричным оператором. Если же схема предполагает обратную связь, т.е. сеть управляемая, или самонастраивающаяся, то вектор R будет вектором управления, замыкающим обратную связь. Определим его регулятором действия элемента сети. На цепи [i, k] имеем

S_i=At-^kS_i+ k + Y^ i A^,_i^+lR_i+ j .                      (5)

Если ввести обозначения

к

Si=^AyRl+],    S^A^St+k, i=i то равенство (5) принимает вид

Si = S,0 + Sl1.                                   (6)

Равенство (6), как и равенство (5), справедливо для любого i 3 N. При этом оператор A[ будет тождественным оператором. С учётом инвариантности равенства для сети в общем виде анализа будем опускать индикатор слоя и полагать управляющее воздействие в каждом модуле системы как свою постоянную величину. При обозначениях y = St,   S0=y0ao,   Sf = у1с11+у2а2 +- + yrar, равенство (6) описывает r-мерный симплекс Ar = (а0, а1,..., а^ [2, стр. 19] в m-мерном евклидовом пространстве Em, r < m, т = т0 +т1 + —+ тп, где mi количество объектов в i-слое.

Нормированное соотношение (6) в пространстве суммируемых с первой степенью последовательностей определяет его как выпуклую линейную комбинацию в барицентрических координатах точки у Е Ar ^ Ет, однозначно характеризуют произвольно выделенный модуль левосторонним идеалом, и определяет сеть геометрическим комплексом, где каждой точке ставится в соответствие ортонормированный базисный вектор (r + 1)-мерного евклидового пространства Rr+ 1,в котором определяется симплекс Er = (eо, ei, _, er) c Rr + 1

У = у ° е₀+у¹е₁+у 2 е 2 +-- + y^re_r, y^r > 0, Х к=о У^к = 1- (7)

На одном и том же комплексе функторами можно задать множество числовых категорий. Категории с соотношениями (7) на объектах назовём стандартными. Две стандартные категории отличаются только деформацией структуры по отношению друг к другу. Любую категорию можно привести к стандартному виду. С другой стороны, при структурной устойчивости системы к возмущениям (например, сохранением амортизационных отчислений), граничные возмущения передаются послойным возмущением объектов.

Пусть при неизменной структуре и стандартном состоянии Y = G ( Ob / N имеют место возмущения X = F ( Ob/N) и на соответствии k = ( X, Y, K), К Q X XY определена мера |(К). Учитывая, что D (у ) = 1, запишем основное метрическое тождество, исходя из показаний математического ожидания и дисперсии в каждом объекте возмущённой сети

D(X) = E2(X) + (^(X}.

Оценить состояние узла сети можно по показателю структурной оценки качества его действия [3]

v(X) = tg 0(X} =

^(X)

E(X)

0(X~) = arctg

^(X)

E(X)