Проявление эффекта аномальной диффузии в поровых жидкостях

1.    Введение1.1.    Диффузия и ЯМР в пористых средах

Применение методов ЯМР позволяет получить детальные сведения о структуре заполненных жидкостью пористых сред [1]. К ним относятся природные микропористые материалы: глинистые, в частности, нефтесодержащие материалы, скальные породы, гетерогенные каталитические вещества, и т.д.

В данной работе по методу ЯМР с применением градиентного поля экспериментально обнаружена, линейная зависимость скорости поперечной релаксации протонной намагниченности от интервала времени т между импульсами в последовательности КПМГ. Показано, что такая зависимость свидетельствует о том, что перенос вещества, осуществляется в режиме сверхдиффузии. Этот режим возникает в результате поверхностной диффузии адсорбируемых молекул, опосредствованной диффузией по объёму жидкости, заполняющей поры («bulk mediated surface diffusion», [2-4]).

• 1.2.    Аномальная диффузия

Спиновое эхо при обычной диффузии

Если основное магнитное поле неоднородно, В = В ( т ) то в результате диффузии угловая скорость прецессии спинов ядер меняется. Это приводит к росту разброса, по фазе, то есть к изменению поперечного времени релаксации:

Т2 ^ т2, где

1       1

— -- + ---.

′ т2 т2 т2D

Рассмотрим применение метода спинового эха к измерению величины T2D. Будем считать, что магнитное поле аксиально симметрично, как, например, вблизи оси соленоида: В = (0, 0, Во + G • z), где G = 8B_Z/dz — градиент поля. Уравнение для намагниченности с учётом диффузии в лабораторной системе отсчёта в случае бесконечно больших времён релаксации имеет вид

М = -у(В х М) + DAM, где D — коэффициент диффузии. Во вращающейся системе отсчёта имеем

M z = 0,

Mix = yGzMy + DAMx, M_y = —yGzM_x + DAM_y .

Теперь учтём релаксацию:

1 ^M z = ^—тр" ^{( M} z ^{- M} z ), ^T1

M_x = yGzM_y + DAM_x - —M_x + DAM_x,

T2

My — — yGzMx — —My + DAMy ,

T2

где M0 — равновесная намагниченность.

Пусть при t = 0 ядра находятся в термодинамическом равновесии и равномерно распределены по образцу, то есть M_Z = M°, M_x = 0, My = 0. В результате короткого импульса л/2 резонансного магнитного поля, направленного во вращающейся системе отсчёта вдоль оси у , возникает однородная, не зависящая от координат намагниченность:

M z = 0, Mx = Mo = M0, My = 0.                     (2)

При t >  0 из-за диффузии она уже не будет однородной. Разделяем переменные, вводя M± =Mx ± iMy/

M+ = —iyGzM+ --M+ + DAM₊ ,                  (3)

T2

(мы интересуемся поперечной релаксацией, поэтому формулы для M_Z далее не приводим). Следуя [5], решение уравнения (3) ищем в виде

M+

t

= Mo exp I — — T2

— iyGzt^ A(t).

Для A(t), с учётом соотношения

A exp(—iyGzt) = —(yGt)² exp(—iyGzt)                       (5)

получаем уравнение

А = —Dy 2G2t2A.

С учётом (2), его решение имеет вид

А = exp ( — ^Dy2G2t³).

Собираем всё вместе

M+ = Mo exp ( — ^- — iyGzt — ¹Dy²G²t3\                  (6)

T2              3

Таким образом, при t = т, имеем

- 3 D7² G^t 3),

М_ж = Mo cos(7Gzt ) exp ( - 1

My = -Mo sin(7GzT) exp ( -   - ¹ D₇ ² G ² t ³

При t = т короткий тг-импульс резонансного поля, направленного снова вдоль оси у, переворачивает M_x, не меняя M_y: M _x ^ -M_x, M_y ^ -M_y. Поэтому, при t = т + 0

	Mx =	-Mo cos(7Gzt ) exp ( - X _ 12	3 D^^T 3),
	My =	-Mo sin(7GzT ) exp ( -   - 12	1 3 D7 2 G 2 t 3),
то есть	M+ =	-Mo exp(i7GzT ) exp ( - — - 12	- 1D72G2 t 3).	(7)

Для нахождения намагниченности при t > т выражение (7) надо взять в качестве начального условия при t = т и снова аналогичным предыдущему способом решить уравнение (3), что даёт (ср. с (6)):

M+ = -Mo exp(i7GzT) exp ( - X - 1D72G2t3) х 123

х exp[-t—- - i7Gz(t - т) - 1D72G2(t - т)3]. 123

Отсюда находим намагниченность при t = 2т:

где

M₊ =

-

^{Mo exp} (- к)-

+ 1D72G2T ².

12    3 Г

Замечательное обстоятельство, составляющее суть эффекта спинового эха, заключается в том, что при t = 2т намагниченность снова становится однородной, не зависящей от координат. Сигнал ЯМР пропорционален величине j dVМ±(r,t)

При t = 2т подынтегральное выражение осциллирует при изменении координаты, поэтому интеграл мал. Осцилляции исчезают при t = 2т, поэтому величина сигнала становится максимальной. Для макроскопического образца это будет резкий всплеск. Сравнивая это выражение с (1), получаем

T2D

= 1D72G2T ².

Затухание спинового эха при аномальной диффузии — формальное описание

Перед обсуждением аномальной диффузии напомним математическое описание обычной диффузии. Пусть при t = 0 молекула находится в точке г = 0. Вероятность того, что в момент t она окажется в элементе объёма dV равна dW = F( r ,t)dV, где плотность вероятности находится из уравнения

Отсюда находим

/ 1 53/2     7      г² \

^F ^Hi^) ^exp( — 4Di)>

< г2 >= 6Dt.

(Ю)

Таким образом, согласно (10), за время t молекула смещается на расстояние

г a t^1/a,

(И)

где а = 2. Эту зависимость легко получить из (9), если по порядку величины заменить

то есть

dF (г,В)    F,

-      .

S - Г д - ч ■ at tг2

Вследствие адсорбции молекулы воды задерживаются у поверхности, поэтому в порах молекула смещается на меньшее расстояние, то есть в этом случае её перемещение характеризуется законом (11) с а >  2. С учётом правил (12), вместо (9) следует писать (см., например, [6]):

^^Т^ = -D_e$$--N^F( г , t),  F( г , 0) = 5( г ).               (13)

Математическое выражение для правой части (13) имеет вид [6]

( АГ 27'(г, t) = jW(г

- r' )F( r' ,t)dV ‘ .

где W( г — г ’) — функция, конкретный вид которой несуществен для дальнейшего анализа. Правая часть (13) сводится к производным от F только при целых значениях показателя степени а/2. Выбор знаков объясняется двумя причинами: 1) При а = 2 получаем снова уравнение (9); 2) Знак минус перед A необходим для вещеетвенности параметра D_eff (см. ниже).

С учётом (13) уравнение (3) в пористой среде принимает вид

М₊ = -^GzM₊ -  М₊ - D_eJJ (-A)“^/2M₊.

Решение этого уравнения снова ищем в виде (4). С учётом (5) получаем

А = -De_ff (yG^A, А = exp ( - D^ ^“G“t“⁺¹ ).

Дальнейший расчёт, аналогичный проделанному в разделе 1.2, приводит к формуле (1), в которой

1.3.    Влияние переноса вещества на скорость релаксации протонной намагниченности

При использовании трехимпульсной последовательности стимулированного эха или последовательности КПМГ скорость релаксации протонной намагниченности жидкости имеет диффузионный вклад (1) [1,7,8]. В отсутствие пористой среды, то есть в неограниченной жидкости, скорость релаксации из-за диффузии в неоднородном поле пропорциональна квадрату временного промежутка между импульсами (8) [8]:

Такая зависимость соответствует нормальной диффузии, при которой расстояние, на которое смещается молекула, пропорционально корню из времени (10) [7]:

I к VDt.

2.    Материалы и методы

В качестве гранул, образующих пористую среду, в работе использованы микрошарики диаметром 57 мкм из кварцевого стекла. Гранулярная пористая среда заполнялась водой и деканом. Для измерения времён релаксации протонной намагниченности поровой жидкости использовали импульсную последовательность КПМГ с переменным временным промежутком т между импульсами. Измерения проводились на спектрометре ЯМР высокого разрешения Varian Inova 500 с частотой резонанса 500 МГц для протонов и диаметром ампулы 5 мм, а также на релаксометре ЯМР Bruker Minispec с частотой резонанса 20 МГц для протонов и диаметром ампулы 20 мм. Микрофотографии образцов получены на детекторе обратно-рассеянных электронов с помощью установки Quanta FEI.

3.    Результаты3.1.    Экспериментальные результаты

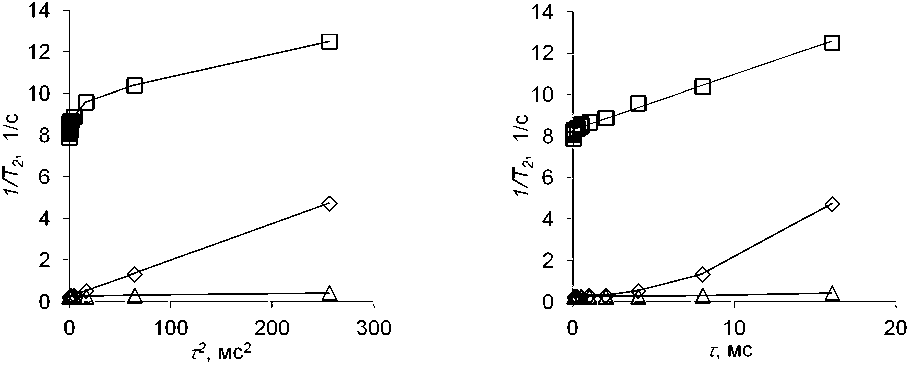
а) б)

Рис. 1. Полученная с использованием спектрометра ЯМР, работающего на частоте протонов 20 МГц, зависимость скорости поперечной релаксации ( 1 /Т2^ протонной намагниченности от квадрата времени между импульсами т ² (а) и от времени т (б) в последовательности КПМГ для свободной воды в условиях «естественной» аппаратной неоднородности постоянного магнитного поля (Д); свободной воды в присутствии искусственно наложенного постоянного градиента магнитного поля по оси X (О); воды в среде стеклянных шариков диаметром 57 мкм (□).

Измерение зависимости скорости поперечной релаксации свободной воды от времени между импульсами в последовательности КПМГ показало применимость соотношения (8)

для свободных жидкостей (рис. 1). На рис. 1 приведены зависимости скоростей релаксации свободной воды в условиях естественной неоднородности магнитного поля и с использованием дополнительного постоянного градиента магнитного поля. Необходимость использования дополнительного градиента обусловлена тем, что естественный (аппаратный) градиент магнитного поля не является постоянным по объёму образца. Как видно из рис. 1, измеренная скорость поперечной релаксации воды в среде стеклянных шариков линейно зависит от времени между импульсами в последовательности КПМГ. Эта зависимость является линейной как для воды, так и для декана, причём справедливость этого факта установлена для разных резонансных частот: 20 МГц и 500 МГц (рис. 2).

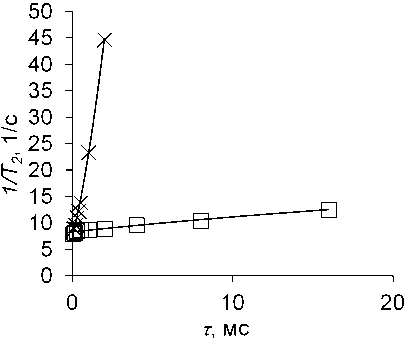
а)

Рис. 2. Линейная зависимость скорости релаксации ( 1 /Т2) протонной намагниченности от временного промежутка между импульсами в последовательности КПМГ в среде из стеклянных шариков для: а) воды и б) декана свидетельствует о сверхдиффузионном режиме переноса вещества. Измерения произведены на спектрометре ЯМР высокого разрешения Varian Inova 500 с частотой резонанса 500 МГц для протонов (х) и на релаксометре ЯМР Bruker Minispec с частотой резонанса 20 МГц для протонов (□)

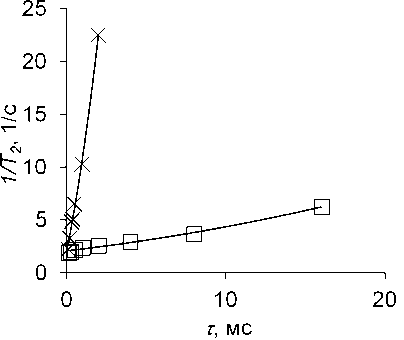
б)

Увеличение диффузионного вклада скорости релаксации при измерениях на приборе с высокой частотой связано, по всей видимости, с повышенной внутренней неоднородностью постоянного магнитного поля, величина которой пропорциональна его индукции [9].

По тангенсам углов наклона прямых на графиках зависимости скорости релаксации от величины промежутка т между импульсами определено отношение градиентов G постоянного магнитного поля, возникающих при измерениях на различных приборах. Отношения градиентов постоянного магнитного поля, рассчитанные с использованием формулы (14) согласуются по порядку величины с отношениями значений индукции магнитного поля (табл. 1).

Т а б л и ц а 1

Отношения градиентов магнитного поля, рассчитанные по зависимостям скорости релаксации воды и декана, заполняющих плотноупакованную гранулярную пористую среду, образованную стеклянными шариками диаметром 57 мкм, от величины т временного промежутка между импульсами в последовательности КПМГ, согласуются по порядку величины с отношениями значений индукции постоянного магнитного поля приборов.

	Вода	Декан
G500M Hz/G20MHZ	60 ± 6	43 ± 4
в500MHz/B20MHZ	25	25

3.2.    Объяснение эффекта сверхдиффузии, наблюдаемой в пористой среде в опытах ЯМР, поставленных по схеме спинового эха

В опытах с шариками диаметром d = 57 мкм наблюдалась зависимость вида (13) с а = 1, соответствующая закону -г х t, то есть сверхдиффузии. В данном разделе этот эффект объясняется в рамках модели, предложенной в работах [2-4], и полученных на её основе результатов.

Следуя [2-4], начнём с рассмотрения простого случая, когда частицы диффундируют в полубесконечном пространстве z >  0 с коэффициентом диффузии D. Обозначим через V иг = (z, p ,t) их среднюю тепловую скорость и радиус-вектор, соответственно. Граница полупространства представляет собой бесконечную плоскость, на которую частица адсорбируется с вероятностью pд при каждом соударении с ней. Положение частицы на плоскости даётся двумерным радиус-вектором p = (х,у\ На плоскости частица находится в течение времени тд и не перемещается по ней. Пусть n(r,t) и ng( p , t) — плотности частиц в пространстве и на плоскости, так что их числа в элементе объёма dV и на элементе площади df равны, соответственно, n(r,t)dV и rig( p ,t)df . Движение частицы описывается уравнениями:

dn(r,t)                   Ә-ng ( p ,t

= ^DAn(r,^t),      ^    = з+ ^{- j}

j+ =7n(z = 0, ppt),  j- =	1 —ng ( p ,t), тд	PдV 7 = 4
Граничное условие на плоскости имеет вид d ( ТГ )   = \ dz ) z=o	: j+ - j-.

Пусть при t = 0 частица в начале координат (0, 0, 0) и адсорбирована на поверхности в точке p = 0. Этому соответствуют начальные условия

п(г, 0) = 0,    ng( p , 0) = d⁽²⁾(p).

Уравнения (15)-(17) решаются путём применения преобразования Фурье по координате p и преобразования Лапласа по времени, что даёт:

n

'"

d?k

W2

+0+г^ ^27.

dpeptn,

ng ( p ,t) =

d?k

W2

• 0+Ж

dpe^ptn g,

где

exp(-qz')    _ = тд(Dq + 7)

d(p, k) , ^g       d(p, k)

^d(p^,k⁾ = ^{(1+ т}дp^)(Dq + 7) ^- 7, q =

r+lD •

Основной вклад в интегралы (18) дают области переменных интегрирования

^k ~ -,  |p| ~ f

Рассмотрим случай

D      г—

— ^ - « v Dt.

Из (19) и (20) заключаем, что при этом справедливы соотношения:

D * k »Д.

„ _      / Dk\ q to k, d(p,k) to yTA\P +--),

V     ^taV

Dt

Tls (p,t)

ТЩ

^2t [ p ^{2 +} (sn )2] ⁷

Из (21) видно, что при условии (20) частица путём прыжков распространяется по поверхности по закону, отличному от фиковского, р ^ Vt

Dt

Р ^ ---,

^TA

Из (20) и (22) заключаем, что режим сверхдиффузии (22) (его иногда называют баллистическим) осуществляется в интервале времени

(утд )² t = (в ) ~ 0,01с

после первого акта адсорбции на поверхность (здесь и далее численные оценки приводятся для значений параметров, характерных для наших опытов: p a ^ 1, t a ^ 10^-8 с, V ~ 3 • 104 см/с). При t > t₀

^ ^{(p,t) to} \(j>A ) ^exp( - 4Dt) ⁽²⁴⁾

то есть при таких временах осуществляется обычная диффузия.

В чём причина отклонения диффузии от режима Фика? Согласно (21), Ng = J dfng pyt) to 1. Из (24) заключаем: Ng to ^ t₀ /^t ^ 0 пр и t ^ ж. Таким образом, при временах (23) частица большую часть времени проводит на поверхности в адсорбированном состоянии, а при t >  to она отрывается от поверхности и находится, в основном, в объёме, диффундируя там обычным образом. Иногда она возвращается на поверхность. Если следить за этими всё более редкими возвратами, то обнаруживается обычная диффузия вдоль поверхности. Ясно, что в этом случае влияние поверхности на характер диффузии незначительно. Напротив, при t <  to взаимодействие частицы с поверхностью резко меняет характер движения частицы.

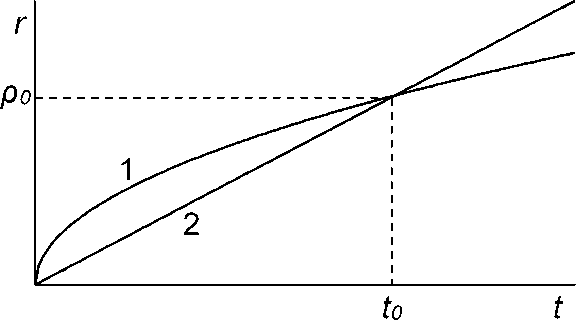
Рис. 3. Распространение частиц при обычной диффузии (кривая 1) и в пористой среде с размером пор меньше р₀ (кривая 2).

5Dto

Ро ~---- ^TA

~ 10 мкм,

(в качестве ро взят радиус круга, на котором находится ~ 3/4 частиц). Поры в среде, состоящей из шариков диаметром d = 57 мкм, имеют размер ~ 6 мкм. Он меньше ро, или, по крайней мере, сравним с ним. Это означает, что после каждого перескока на другую поверхность режим сверхдиффузии вдоль поверхности возобновляется.

Движение частиц в режиме сверхдиффузии вовсе не означает, что оно происходит быстрее, чем при обычной диффузии. Суть дела пояснена на рис. 3. В рассматриваемом здесь случае выполняется условие t < to, поэтому распространение частиц характеризуется прямой линией 2. Поскольку при данном t r2(t) < ri(t), адсорбция замедляет распространение частиц в поре.

4.    Выводы

Экспериментально обнаружен и теоретически обоснован сверхдиффузионный режим переноса молекул воды в порах с размерами dp <  10 мкм при временах меньше 10 мс. Это необходимо учитывать при изучении процессов, происходящих в пористых материалах.